The motion of a body under the action of gravity is one of the central topics in dynamic physics. Even an ordinary schoolboy knows that the section of dynamics is based on Newton's three laws. Let's try to understand this topic thoroughly, and an article describing each example in detail will help us make studying the movement of a body under the influence of gravity as useful as possible.
A bit of history
From time immemorial, people have observed with curiosity the various phenomena occurring in our lives. Mankind for a long time could not understand the principles and structure of many systems, but a long way of studying the world around us led our ancestors to a scientific revolution. Nowadays, when technology is developing at an incredible speed, people hardly think about how certain mechanisms work.

Meanwhile, our ancestors have always been interested in the mysteries of natural processes and the structure of the world, looking for answers to the most difficult questions and did not stop studying until they found answers to them. For example, the famous scientistGalileo Galilei in the 16th century wondered: "Why do bodies always fall down, what force attracts them to the ground?" In 1589, he set up a series of experiments, the results of which proved to be very valuable. He studied in detail the patterns of free fall of various bodies, dropping objects from the famous tower in the city of Pisa. The laws that he deduced were improved and described in more detail by formulas by another famous English scientist - Sir Isaac Newton. It is he who owns the three laws on which almost all modern physics is based.

The fact that the laws of motion of bodies, described more than 500 years ago, are relevant to this day, means that our planet obeys the same laws. A modern person needs to at least superficially study the basic principles of arranging the world.
Basic and auxiliary concepts of dynamics
In order to fully understand the principles of such a movement, you should first familiarize yourself with some concepts. So, the most necessary theoretical terms:
- Interaction is the impact of bodies on each other, in which there is a change or the beginning of their movement relative to each other. There are four types of interaction: electromagnetic, weak, strong and gravitational.
- Speed is a physical quantity that indicates the speed with which a body moves. Velocity is a vector, meaning it has not only a value, but also a direction.
- Acceleration is the quantity thatshows us the rate of change in the speed of the body in a period of time. It is also a vector quantity.
- The trajectory of the path is a curve, and sometimes a straight line, that the body outlines when moving. With uniform rectilinear motion, the trajectory may coincide with the displacement value.
- The path is the length of the trajectory, that is, exactly as much as the body has traveled in a certain amount of time.
- The inertial frame of reference is an environment in which Newton's first law is fulfilled, that is, the body retains its inertia, provided that all external forces are completely absent.
The above concepts are quite enough to correctly draw or imagine in your head a simulation of the movement of a body under the influence of gravity.

What does strength mean?
Let's move on to the main concept of our topic. So, force is a quantity, the meaning of which is the impact or influence of one body on another quantitatively. And gravity is the force that acts on absolutely every body located on the surface or near our planet. The question arises: where does this power come from? The answer lies in the law of gravity.
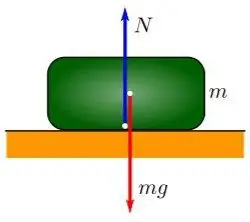
What is gravity?
Any body from the side of the Earth is affected by the gravitational force, which tells it some acceleration. Gravity always has a vertical downward direction, towards the center of the planet. In other words, gravity pulls objects towards the earth, which is why objects always fall down. It turns out that the force of gravity is a special case of the force of universal gravitation. Newton deduced one of the main formulas for finding the force of attraction between two bodies. It looks like this: F=G(m1 x m2) / R 2.
What is the free fall acceleration?
A body that is released from a certain height always flies down under the influence of gravity. The movement of a body under the action of gravity vertically up and down can be described by equations, where the main constant will be the value of the acceleration "g". This value is due solely to the action of the force of attraction, and its value is approximately 9.8 m/s2. It turns out that a body thrown from a height without an initial speed will move down with an acceleration equal to the value "g".
Movement of a body under the action of gravity: formulas for solving problems
The basic formula for finding the force of gravity is as follows: Fgravity =m x g, where m is the mass of the body on which the force acts, and "g" is the acceleration of free fall (to simplify tasks, it is considered to be equal to 10 m/s2).
There are several more formulas used to find one or another unknown in the free movement of the body. So, for example, in order to calculate the path traveled by the body, it is necessary to substitute known values into this formula: S=V0 x t + a x t2 / 2 (the path is equal to the sum of the products of the initial speed multiplied by time and acceleration by the square of time divided by 2).
Equations for describing the vertical motion of a body
The movement of a body under the influence of gravity along the vertical can be described by an equation that looks like this: x=x0 + v0 x t + a x t2 / 2. Using this expression, you can find the coordinates of the body at a known point in time. You just need to substitute the values known in the problem: the initial location, the initial speed (if the body was not just released, but pushed with some force) and acceleration, in our case it will be equal to the acceleration g.
In the same way, you can find the speed of a body that moves under the influence of gravity. The expression for finding an unknown value at any time: v=v0 + g x t which the body moves).
Movement of bodies under the action of gravity: tasks and methods for their solutions
For many problems involving gravity, we recommend using the following plan:
- Determine for yourself a convenient inertial frame of reference, it is usually customary to choose the Earth, because it meets many of the requirements for ISO.
- Draw a small drawing or drawing showing the main forces,acting on the body. The movement of a body under the influence of gravity implies a sketch or diagram that indicates in which direction the body moves if it is subjected to an acceleration equal to g.
- Then you should choose the direction for projecting forces and resulting accelerations.
- Write unknown quantities and determine their direction.
- Finally, using the formulas above to solve problems, calculate all unknowns by substituting the data into the equations to find the acceleration or distance traveled.
Ready-to-use solution for an easy task
When it comes to such a phenomenon as the movement of a body under the influence of gravity, determining which way is more practical to solve the problem at hand can be difficult. However, there are a few tricks, using which you can easily solve even the most difficult task. So, let's take a look at live examples of how to solve a particular problem. Let's start with an easy to understand problem.
Some body was released from a height of 20 m without initial velocity. Determine how much time it will take to reach the ground.
Solution: we know the path traveled by the body, we know that the initial speed was 0. We can also determine that only gravity acts on the body, it turns out that this is the movement of the body under the influence of gravity, and therefore we should use this formula: S=V0 x t + a x t2/2. Since in our case a=g, after some transformations we obtain the following equation: S=g x t2 / 2. Nowit remains only to express the time through this formula, we get that t2 =2S / g. Substitute the known values (we assume that g=10 m/s2) t2=2 x 20 / 10=4. Therefore, t=2 s.
So our answer is: the body will fall to the ground in 2 seconds.
A trick that allows you to quickly solve the problem is as follows: you can see that the described movement of the body in the above problem occurs in one direction (vertically down). It is very similar to uniformly accelerated motion, since no force acts on the body, except for gravity (we neglect the force of air resistance). Thanks to this, you can use an easy formula to find the path with uniformly accelerated motion, bypassing the images of drawings with the arrangement of forces acting on the body.
An example of solving a more complex problem
Now let's see how best to solve problems on the movement of a body under the influence of gravity, if the body does not move vertically, but has a more complex movement pattern.
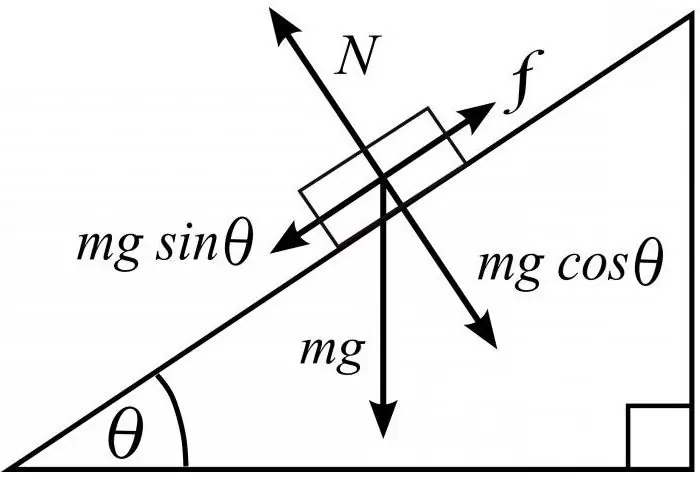
For example, the following problem. An object of mass m is moving with unknown acceleration down an inclined plane whose coefficient of friction is k. Determine the value of the acceleration that is present when the given body moves, if the angle of inclination α is known.
Solution: Use the plan above. First of all, draw a drawing of an inclined plane with the image of the body and all the forces acting on it. It turns out that three components act on it:gravity, friction and support reaction force. The general equation of the resultant forces looks like this: Ffriction + N + mg=ma.
The main highlight of the problem is the slope condition at the angle α. When projecting forces onto the ox axis and the oy axis, this condition must be taken into account, then we will get the following expression: mg x sin α - Ffriction =ma (for the x axis) and N - mg x cos α=Ffriction (for oy axis).
Ffriction is easy to calculate by the formula for finding the friction force, it is equal to k x mg (friction coefficient multiplied by the product of body mass and free fall acceleration). After all the calculations, it remains only to substitute the found values into the formula, you will get a simplified equation for calculating the acceleration with which the body moves along the inclined plane.






