Movement of the body at an angle to the horizon: formulas, calculation of flight range and maximum takeoff altitude

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

When studying mechanical motion in physics, after getting acquainted with the uniform and uniformly accelerated movement of objects, they proceed to consider the motion of a body at an angle to the horizon. In this article, we will study this issue in more detail.

What is the motion of a body at an angle to the horizon?

This type of object movement occurs when a person throws a rock into the air, a cannon fires a cannon ball, or a goalkeeper kicks a soccer ball out of the goal. All such cases are considered by the science of ballistics.

The noted type of movement of objects in the air occurs along a parabolic trajectory. In the general case, carrying out the corresponding calculations is not an easy task, since it is necessary to take into account air resistance, the rotation of the body during flight, the rotation of the Earth around its axis, and some other factors.

In this article, we will not take into account all these factors, but consider the issue from a purely theoretical point of view. However, the resulting formulas are quite gooddescribe the trajectories of bodies moving over short distances.

Obtaining formulas for the considered type of movement

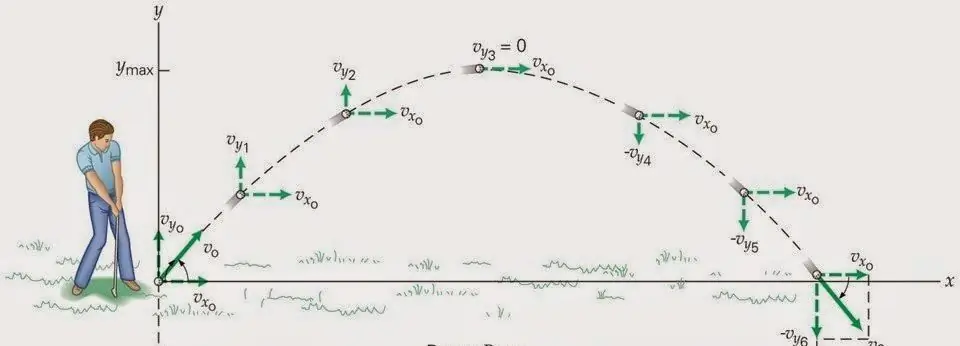
Let's derive the formulas for the movement of the body to the horizon at an angle. In this case, we will take into account only one single force acting on a flying object - gravity. Since it acts vertically downwards (parallel to the y-axis and against it), then, considering the horizontal and vertical components of the movement, we can say that the first will have the character of a uniform rectilinear movement. And the second - equally slow (evenly accelerated) rectilinear movement with acceleration g. That is, the velocity components through the value v₀ (initial speed) and θ (the angle of the body movement direction) will be written as follows:

v_x=v₀cos(θ)

v_y=v₀sin(θ)-gt

The first formula (for v_x) is always valid. As for the second one, one nuance should be noted here: the minus sign before the product gt is put only if the vertical component v₀sin(θ) is directed upwards. In most cases, this happens, however, if you throw a body from a height, pointing it down, then in the expression for v_y you should put a "+" sign before gt.

Integrating the formulas for the velocity components over time, and taking into account the initial height h of the body flight, we obtain the equations for the coordinates:

x=v₀cos(θ)t

y=h+v₀sin(θ)t-gt²/2

Calculate flight range

When considering in physics the movement of a body to the horizon at an angle useful for practical use, it turns out to calculate the flight range. Let's define it.

Since this movement is a uniform movement without acceleration, it is enough to substitute the flight time into it and get the desired result. Flight range is determined solely by movement along the x-axis (parallel to the horizon).

The time the body is in the air can be calculated by equating the y coordinate to zero. We have:

0=h+v₀sin(θ)t-gt²/2

This quadratic equation is solved through the discriminant, we get:

D=b²- 4ac=v₀²sin ²(θ) - 4(-g/2)h=v₀² sin²(θ) + 2gh, t=(-b±√D)/(2a)=(-v₀sin(θ)±√(v₀ ²sin²(θ) + 2gh))/(-2g/2)=

=(v₀sin(θ)+√(v₀² sin²(θ) + 2gh))/g.

In the last expression, one root with a minus sign is discarded, due to its insignificant physical value. Substituting the flight time t into the expression for x, we get the flight range l:

l=x=v₀cos(θ)(v₀sin(θ)+√(v ₀²sin²(θ) + 2gh))/g.

The easiest way to analyze this expression is if the initial heightis equal to zero (h=0), then we get a simple formula:

l=v ₀²sin(2θ)/g

This expression indicates that the maximum flight range can be obtained if the body is thrown at an angle of 45^o(sin(245^o)=m1).

Max body height

Besides the flight range, it is also useful to find the height above the ground that the body can rise to. Since this type of movement is described by a parabola, the branches of which are directed downwards, the maximum lifting height is its extremum. The latter is calculated by solving the equation for the derivative with respect to t for y:

dy/dt=d(h+v₀sin(θ)t-gt²/2)/dt=v₀sin(θ)-gt=0=>

=>t=v₀sin(θ)/g.

Substitute this time into the equation for y, we get:

y=h+v₀sin(θ)v₀sin(θ)/g-g(v ₀sin(θ)/g)²/2=h + v₀ ²sin²(θ)/(2g).

This expression indicates that the body will rise to the maximum height if it is thrown vertically upwards (sin²(90^o)=1).