The world in which we live is unimaginably beautiful and full of many different processes that set the course of life. All these processes are studied by the familiar science - physics. It provides an opportunity to get at least some idea of the origin of the universe. In this article, we will consider such a concept as molecular-kinetic theory, its equations, types and formulas. However, before moving on to a deeper study of these issues, you need to clarify for yourself the very meaning of physics and the areas it studies.
What is physics?

In fact, this is a very extensive science and, perhaps, one of the most fundamental in the history of mankind. For example, if the same computer science is associated with almost every area of human activity, whether it is computational design or the creation of cartoons, then physics is life itself, a description of its complex processes and flows. Let's try to make out its meaning, simplifying the understanding as much as possible.
SoThus, physics is a science that deals with the study of energy and matter, the connections between them, the explanation of many processes occurring in our vast universe. The molecular-kinetic theory of the structure of matter is only a small drop in the sea of theories and branches of physics.
Energy, which this science studies in detail, can be represented in a variety of forms. For example, in the form of light, motion, gravity, radiation, electricity and many other forms. We will touch upon in this article the molecular kinetic theory of the structure of these forms.
The study of matter gives us an idea of the atomic structure of matter. By the way, it follows from the molecular-kinetic theory. The science of the structure of matter allows us to understand and find the meaning of our existence, the reasons for the emergence of life and the Universe itself. Let's still try to study the molecular kinetic theory of matter.
First, some introduction is needed to fully understand the terminology and any conclusions.
Physics topics
Answering the question of what molecular-kinetic theory is, one cannot but talk about sections of physics. Each of these deals with the detailed study and explanation of a particular area of human life. They are classified as follows:
- Mechanics, which is divided into two more sections: kinematics and dynamics.
- Static.
- Thermodynamics.
- Molecular section.
- Electrodynamics.
- Optics.
- Physics of quantums and the atomic nucleus.
Let's talk specifically about molecularphysics, because it is based on the molecular-kinetic theory.
What is thermodynamics?
In general, the molecular part and thermodynamics are closely related branches of physics, which study exclusively the macroscopic component of the total number of physical systems. It is worth remembering that these sciences describe precisely the internal state of bodies and substances. For example, their state during heating, crystallization, vaporization and condensation, at the atomic level. In other words, molecular physics is the science of systems that consist of a huge number of particles: atoms and molecules.
It was these sciences that studied the main provisions of the molecular kinetic theory.
Even in the course of the seventh grade, we got acquainted with the concepts of micro- and macro-worlds, systems. It will not be superfluous to refresh these terms in memory.
The microworld, as we can see from its very name, is made up of elementary particles. In other words, this is the world of small particles. Their sizes are measured in the range from 10-18 m to 10-4 m, and the time of their actual state can reach both infinity and disproportionately small intervals, for example, 10-20 s.
Macroworld considers bodies and systems of stable forms, consisting of many elementary particles. Such systems are commensurate with our human size.
In addition, there is such a thing as a mega world. It is made up of vast planets, cosmic galaxies and complexes.
Basicstheory
Now that we've recapped a little and remembered the basic terms of physics, we can go directly to the main topic of this article.
Molecular-kinetic theory appeared and was formulated for the first time in the nineteenth century. Its essence lies in the fact that it describes in detail the structure of any substance (more often the structure of gases than solid and liquid bodies), based on three fundamental provisions that were collected from the assumptions of such prominent scientists as Robert Hooke, Isaac Newton, Daniel Bernoulli, Mikhail Lomonosov and many others.
The main provisions of the molecular kinetic theory sound like this:
- Absolutely all substances (regardless of whether they are liquid, solid or gaseous) have a complex structure, consisting of smaller particles: molecules and atoms. Atoms are sometimes called "elementary molecules".
- All these elementary particles are always in a state of continuous and chaotic movement. Each of us has come across a direct proof of this proposition, but, most likely, did not attach much importance to it. For example, we all saw against the background of the sun's rays that dust particles are constantly moving in a chaotic direction. This is due to the fact that the atoms produce mutual pushes with each other, constantly imparting kinetic energy to each other. This phenomenon was first studied in 1827, and it was named after the discoverer - "Brownian motion".
- All elementary particles are in the process of continuous interaction with each other withcertain forces that have an electrical rock.
It is worth noting that another example describing position number two, which may also apply, for example, to the molecular kinetic theory of gases, is diffusion. We encounter it in everyday life, and in multiple tests and controls, so it is important to have an idea about it.
First, consider the following examples:
The doctor accidentally spilled alcohol from a flask on the table. Or maybe you dropped your perfume bottle and it spread all over the floor.
Why, in these two cases, both the smell of alcohol and the smell of perfume will fill the whole room after some time, and not just the area where the contents of these substances were spilled?
The answer is simple: diffusion.
Diffusion - what is it? How does it flow?

This is a process in which the particles that make up one particular substance (usually a gas) penetrate into the intermolecular voids of another. In our examples above, the following happened: due to thermal, that is, continuous and dissociated movement, alcohol and / or perfume molecules fell into the gaps between air molecules. Gradually, under the influence of collision with atoms and molecules of air, they spread around the room. By the way, the intensity of diffusion, that is, the speed of its flow, depends on the density of the substances involved in diffusion, as well as on the energy of motion of their atoms and molecules, called kinetic. The greater the kinetic energy, the higher the speed of these molecules, respectively, and the intensity.
The fastest diffusion process can be called diffusion in gases. This is due to the fact that the gas is not homogeneous in its composition, which means that intermolecular voids in gases occupy a significant amount of space, respectively, and the process of getting atoms and molecules of a foreign substance into them proceeds easier and faster.
This process is a little slower in liquids. The dissolution of sugar cubes in a mug of tea is just an example of the diffusion of a solid in a liquid.
But the longest time is diffusion in bodies with a solid crystalline structure. This is exactly so, because the structure of solids is homogeneous and has a strong crystal lattice, in the cells of which the atoms of the solid vibrate. For example, if the surfaces of two metal bars are cleaned well and then brought into contact with each other, then after a sufficiently long time we will be able to detect pieces of one metal in the other, and vice versa.
Like any other fundamental section, the basic theory of physics is divided into separate parts: classification, types, formulas, equations, and so on. Thus, we have learned the basics of molecular kinetic theory. This means that you can safely move on to the consideration of individual theoretical blocks.
Molecular-kinetic theory of gases
There is a need to understand the provisions of the gas theory. As we said earlier, we will consider the macroscopic characteristics of gases, such as pressure and temperature. This iswill be needed later in order to derive the equation of the molecular-kinetic theory of gases. But mathematics - later, and now let's deal with theory and, accordingly, physics.
Scientists have formulated five provisions of the molecular theory of gases, which serve to comprehend the kinetic model of gases. They sound like this:
- All gases are made up of elementary particles that do not have a certain size, but have a certain mass. In other words, the volume of these particles is minimal compared to the length between them.
- Atoms and molecules of gases have practically no potential energy, respectively, according to the law, all energy is equal to kinetic.
- We already got acquainted with this position earlier - Brownian motion. That is, gas particles are always in continuous and chaotic motion.
- Absolutely all mutual collisions of gas particles, accompanied by the message of speed and energy, are completely elastic. This means that there is no loss of energy or sharp jumps in their kinetic energy during a collision.
- Under normal conditions and constant temperature, the average energy of particle motion of almost all gases is the same.
We can rewrite the fifth position through this type of equation of the molecular-kinetic theory of gases:
E=1/2mv^2=3/2kT, where k is the Boltzmann constant; T - temperature in Kelvin.
This equation makes us understand the relationship between the speed of elementary particles of gas and their absolute temperature. Accordingly, the higher their absolutetemperature, the greater their speed and kinetic energy.
Gas pressure
Such macroscopic components of the characteristic, such as the pressure of gases, can also be explained using the kinetic theory. To do this, let's imagine the following example.
Let's assume that a molecule of some gas is in a box, the length of which is L. Let's use the provisions of the gas theory described above and take into account the fact that the molecular sphere moves only along the x-axis. Thus, we will be able to observe the process of elastic collision with one of the walls of the vessel (box).
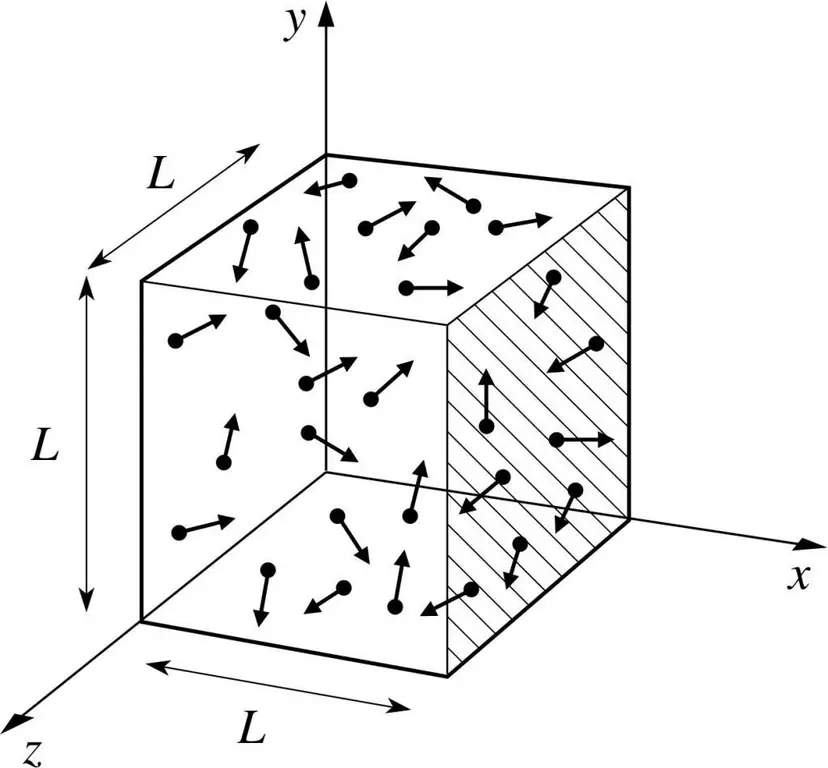
The momentum of the ongoing collision, as we know, is determined by the formula: p=mv, but in this case, this formula will take on a projection form: p=mv(x).
Since we consider only the dimension of the x-axis, that is, the x-axis, the total change in momentum will be expressed by the formula: mv(x) - m(-v(x))=2mv(x).
Next, consider the force exerted by our object using Newton's second law: F=ma=P/t.
From these formulas we express the pressure from the gas side: P=F/a;
Now let's substitute the force expression into the resulting formula and get: P=mv(x)^2/L^3.
After that, our finished pressure formula can be written for the N-th number of gas molecules. In other words, it will look like this:
P=Nmv(x)^2/V, where v is speed and V is volume.
Now let's try to highlight a few basic provisions on gas pressure:
- It manifests itself throughcollisions of molecules with molecules of the walls of the object in which it is located.
- The magnitude of pressure is directly proportional to the force and speed of impact of molecules on the walls of the vessel.
Some brief conclusions on theory
Before we go further and consider the basic equation of molecular kinetic theory, we offer you a few brief conclusions from the above points and theory:
- The measure of the average energy of motion of its atoms and molecules is the absolute temperature.
- When two different gases are at the same temperature, their molecules have the same average kinetic energy.
- The energy of gas particles is directly proportional to the root mean square velocity: E=1/2mv^2.
- Although gas molecules have an average kinetic energy, respectively, and an average speed, individual particles move at different speeds: some fast, some slow.
- The higher the temperature, the higher the speed of the molecules.
- How many times we increase the temperature of the gas (for example, double), the energy of motion of its particles increases as many times (respectively, doubles).
Basic equation and formulas

The basic equation of the molecular kinetic theory allows you to establish the relationship between the quantities of the microworld and, accordingly, the macroscopic, that is, measured, quantities.
One of the simplest models that molecular theory can consider is the ideal gas model.
You could say thatthis is a kind of imaginary model studied by the molecular kinetic theory of an ideal gas, in which:
- the simplest gas particles are considered as perfectly elastic balls that interact both with each other and with the molecules of the walls of any vessel in only one case - an absolutely elastic collision;
- the forces of attraction inside the gas are absent, or they can actually be neglected;
- elements of the internal structure of the gas can be taken as material points, that is, their volume can also be neglected.
Considering such a model, German-born physicist Rudolf Clausius wrote a formula for gas pressure through the relationship of micro- and macroscopic parameters. It looks like:
p=1/3m(0)nv^2.
Later this formula will be called as the basic equation of the molecular-kinetic theory of an ideal gas. It can be presented in several different forms. Our duty now is to show sections such as molecular physics, molecular kinetic theory, and hence their complete equations and types. Therefore, it makes sense to consider other variations of the basic formula.
We know that the average energy characterizing the motion of gas molecules can be found using the formula: E=m(0)v^2/2.
In this case, we can replace the expression m(0)v^2 in the original pressure formula with the average kinetic energy. As a result of this, we will have the opportunity to compose the basic equation of the molecular kinetic theory of gases in the following form: p=2/3nE.
Besides, you and I know that the expression m(0)n can be written as a product of two quotients:
m/NN/V=m/V=ρ.
After these manipulations, we can rewrite our formula for the equation of the molecular-kinetic theory of an ideal gas in a third, different form:
p=1/3ρv^2.
Well, perhaps that's all you need to know on this topic. It remains only to systematize the knowledge gained in the form of brief (and not so) conclusions.
All general conclusions and formulas on the topic "Molecular-kinetic theory"
So let's get started.
First:
Physics is a fundamental science included in the course of natural science, which studies the properties of matter and energy, their structure, patterns of inorganic nature.
It includes the following sections:
- mechanics (kinematics and dynamics);
- static;
- thermodynamics;
- electrodynamics;
- molecular section;
- optics;
- physics of quantums and the atomic nucleus.
Second:
Particle physics and thermodynamics are closely related branches that study the exclusively macroscopic component of the total number of physical systems, that is, systems consisting of a huge number of elementary particles.
They are based on molecular kinetic theory.
Third:
The crux of the matter is this. Molecular-kinetic theory describes in detail the structure of a substance (more often the structure of gases than solids).and liquid bodies), based on three fundamental assumptions that were collected from the assumptions of prominent scientists. Among them: Robert Hooke, Isaac Newton, Daniel Bernoulli, Mikhail Lomonosov and many others.
Fourth:
Three basic tenets of molecular kinetic theory:
- All substances (regardless of whether they are liquid, solid or gaseous) have a complex structure consisting of smaller particles: molecules and atoms.
- All these simple particles are in continuous chaotic motion. Example: Brownian motion and diffusion.
- All molecules under any conditions interact with each other with certain forces that have an electric rock.
Each of these provisions of the molecular kinetic theory is a solid foundation in the study of the structure of matter.
Fifth:
Several main points of molecular theory for the gas model:
- All gases are made up of elementary particles that do not have a certain size, but have a certain mass. In other words, the volume of these particles is minimal compared to the distances between them.
- Atoms and molecules of gases have practically no potential energy, respectively, their total energy is equal to the kinetic one.
- We already got acquainted with this position earlier - Brownian motion. That is, gas particles are always in continuous and random motion.
- Absolutely all mutual collisions of atoms and molecules of gases, accompanied by the message of speed and energy, are completely elastic. This ismeans that there is no loss of energy or sharp jumps in their kinetic energy during a collision.
- Under normal conditions and constant temperature, the average kinetic energy of almost all gases is the same.
Sixth:
Conclusions from the theory on gases:
- Absolute temperature is a measure of the average kinetic energy of its atoms and molecules.
- When two different gases are at the same temperature, their molecules have the same average kinetic energy.
- The average kinetic energy of gas particles is directly proportional to the root mean square velocity: E=1/2mv^2.
- Although gas molecules have an average kinetic energy, respectively, and an average speed, individual particles move at different speeds: some fast, some slow.
- The higher the temperature, the higher the speed of the molecules.
- How many times we increase the temperature of a gas (for example, doubling), the average kinetic energy of its particles also increases by that many times (respectively, doubles).
- The relationship between the pressure of a gas on the walls of the vessel in which it is located and the intensity of impacts of molecules on these walls is directly proportional: the more impacts, the higher the pressure, and vice versa.
Seventh:
An ideal gas model is a model in which the following conditions must be met:
- Gas molecules can and are considered as perfectly elastic balls.
- These balls can interact with each other and with the walls of anyvessel in only one case - absolutely elastic collision.
- Those forces that describe the mutual thrust between atoms and molecules of a gas are absent or can actually be neglected.
- Atoms and molecules are considered as material points, that is, their volume can also be neglected.
Eighth:
Let's give all the basic equations and show the formulas in the topic "Molecular-kinetic theory":
p=1/3m(0)nv^2 - the basic equation for the ideal gas model, derived by the German physicist Rudolf Clausius.
p=2/3nE - the basic equation of the molecular-kinetic theory of an ideal gas. Derived from the average kinetic energy of the molecules.
р=1/3ρv^2 - the same equation, but considered through the density and root mean square velocity of ideal gas molecules.
m(0)=M/N(a) - the formula for finding the mass of one molecule through the Avogadro number.
v^2=(v(1)+v(2)+v(3)+…)/N - formula for finding the mean square velocity of molecules, where v(1), v(2), v (3) and so on - the speed of the first molecule, the second, the third and so on up to the nth molecule.
n=N/V - formula for finding the concentration of molecules, where N is the number of molecules in a gas volume to a given volume V.
E=mv^2/2=3/2kT - formulas for finding the average kinetic energy of molecules, where v^2 is the root mean square velocity of molecules, k is a constant value named after the Austrian the physics of Ludwig Boltzmann, and T is the temperature of the gas.
p=nkT - pressure formula in terms of concentration, constantBoltzmann and the absolute temperature T. From it follows another fundamental formula, discovered by the Russian scientist Mendeleev and the French physicist-engineer Claiperon:
pV=m/MRT, where R=kN(a) is the universal constant for gases.
Now let's show constants for different iso-processes: isobaric, isochoric, isothermal and adiabatic.
pV/T=const - performed when the mass and composition of the gas are constant.
рV=const - if the temperature is also constant.
V/T=const - if gas pressure is constant.
p/T=const - if volume is constant.
Perhaps that's all you need to know on this topic.
Today we plunged into such a scientific field as theoretical physics, its multiple sections and blocks. In more detail, we touched upon such an area of physics as fundamental molecular physics and thermodynamics, namely, molecular-kinetic theory, which, it would seem, does not present any difficulties in the initial study, but in fact has many pitfalls. It expands our understanding of the ideal gas model, which we also studied in detail. In addition, it is worth noting that we also got acquainted with the basic equations of molecular theory in their various variations, and also considered all the most necessary formulas for finding certain unknown quantities on this topic. This will be especially useful in preparing for writing any tests, examinations and tests, or to expand the general outlook and knowledge of physics.
We hope that this article was useful to you, and you have extracted only the most necessary information from it, strengthening your knowledge in such pillars of thermodynamics as the basic provisions of molecular kinetic theory.






