Sometimes it seems that our world is simple and clear. In fact, this is the great mystery of the Universe that created such a perfect planet. Or maybe it was created by someone who probably knows what he is doing? The greatest minds of our time are working on this question.

They each time come to the conclusion that it is impossible to create everything that we have without the Supreme mind. What an extraordinary, complex and at the same time simple and direct our planet Earth! The world around us is amazing with its rules, shapes, colors.
Laws of nature
The first thing you can notice about our huge and amazing planet is axial symmetry. It is found in all forms of the surrounding world, and is also the basic principle of beauty, ideality and proportionality. This is nothing but mathematics in nature.
The concept of "symmetry" means harmony, correctness. This is a property of the surrounding reality, systematizing fragments and turning them into a single whole. Even in ancient Greece, signs of this law began to be noticed for the first time. For example, Plato believed that beauty appears exclusivelydue to symmetry and proportion. In fact, if we look at objects that are proportionate, correct and complete, then our internal state will be beautiful.
The laws of mathematics in animate and inanimate nature
Let's take a look at any creature, for example, the most perfect - a man. We will see the structure of the body, which looks the same on both sides. You can also list many samples, such as insects, animals, marine life, birds. Each species has its own color.

If any pattern or pattern is present, it is known to be mirrored about the center line. All organisms are created due to the rules of the universe. Such mathematical patterns can be traced in inanimate nature.
If you pay attention to all the phenomena, such as a tornado, a rainbow, plants, snowflakes, you can find a lot in common in them. Regarding the axis of symmetry, the leaf of the tree is divided in half, and each part will be a reflection of the previous one.

Also, if we take as an example a tornado that rises vertically and looks like a funnel, then it can also be conditionally divided into two absolutely identical halves. You can meet the phenomenon of symmetry in the change of day and night, the seasons. The laws of the surrounding world are mathematics in nature, which has its own perfect system. The whole concept of the creation of the Universe is based on it.
Rainbow
We rarely think about natural phenomena. It snowed or rained, looked outthe sun or thunder struck - the usual state of changing weather. Consider a multi-colored arc that can usually be found after precipitation. A rainbow in the sky is an amazing natural phenomenon, accompanied by a spectrum of all colors visible only to the human eye. This happens due to the passage of the rays of the sun through the outgoing cloud. Each raindrop serves as a prism that has optical properties. We can say that any drop is a small rainbow.

When passing through a water barrier, the rays change their original color. Every stream of light has a certain length and shade. Therefore, our eye perceives the rainbow as such a multi-colored one. Note the interesting fact that this phenomenon can only be seen by a person. Because it's just an illusion.
Types of rainbows
- Rainbows formed from the sun are the most common. It is the brightest of all varieties. Consists of seven primary colors: red orange, yellow, green, blue, indigo, violet. But if you look at the details, there are much more shades than our eyes can see.
- A rainbow created by the moon occurs at night. It is believed that it can always be seen. But, as practice shows, basically this phenomenon is observed only in rainy areas or near large waterfalls. The colors of the lunar rainbow are very dull. They are destined to be considered only with the help of special equipment. But even with it, our eye can only make out a strip of white.
- The rainbow, which appeared as a result of fog, is like a wide shining light arch. Sometimes this type is confused with the previous one. From above, the color can be orange, from below it can have a shade of purple. The sun's rays, passing through the fog, form a beautiful natural phenomenon.
- Fiery rainbow in the sky is extremely rare. It is not similar to the previous species in its horizontal shape. You can only see this phenomenon above cirrus clouds. They usually extend at an altitude of 8-10 kilometers. The angle at which the rainbow will show itself in all its glory must be more than 58 degrees. The colors usually stay the same as in the solar rainbow.
Golden Ratio (1, 618)
Perfect proportion is most often found in the animal world. They are awarded such a proportion, which is equal to the root of the corresponding number of PHI to one. This ratio is the connecting fact of all animals on the planet. The great minds of antiquity called this number the divine proportion. It can also be called the golden ratio.
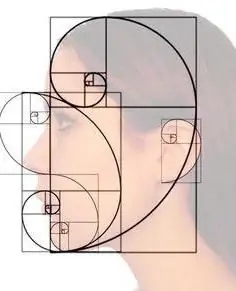
This rule is fully consistent with the harmony of the human structure. For example, if you determine the distance between the eyes and eyebrows, then it will be equal to the divine constant.
The golden ratio is an example of how important mathematics is in nature, the law of which designers, artists, architects, creators of beautiful and perfect things began to follow. They create with the help of the divine constant their creations, which are balanced, harmonious and pleasant to look at. Our mind can countbeautiful are those things, objects, phenomena, where there is an unequal ratio of parts. Proportionality is what our brain calls the golden ratio.
DNA helix
As the German scientist Hugo Weil rightly noted, the roots of symmetry came through mathematics. Many noted the perfection of geometric figures and paid attention to them. For example, a honeycomb is nothing more than a hexagon created by nature itself. You can also pay attention to the cones of spruce, which have a cylindrical shape. Also, a spiral is often found in the outside world: horns of large and small livestock, mollusk shells, DNA molecules.

The DNA helix is created according to the principle of the golden ratio. It is a link between the scheme of the material body and its real image. And if we consider the brain, then it is nothing more than a conductor between the body and the mind. The intellect connects life and the form of its manifestation and allows the life contained in the form to know itself. With the help of this, humanity can understand the surrounding planet, look for patterns in it, which are then applied to the study of the inner world.
Fission in nature
Cell mitosis consists of four phases:
- Prophase. It increases the core. Chromosomes appear, which begin to twist into a spiral and turn into their ordinary form. A place is formed for cell division. At the end of the phase, the nucleus and its membrane dissolve, and the chromosomes flow into the cytoplasm. This is the longest division stage.
- Metaphase. Here the twisting into a spiral of chromosomes ends, they form a metaphase plate. The chromatids line up opposite each other in preparation for division. Between them there is a place for disconnection - a spindle. This concludes the second stage.
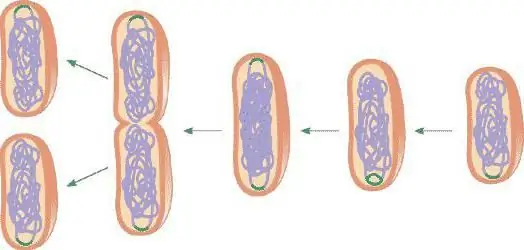
- Anaphase. The chromatids move in opposite directions. Now the cell has two sets of chromosomes due to their division. This stage is very short.
- Telophase. In each half of the cell, a nucleus is formed, inside which the nucleolus is formed. The cytoplasm is actively dissociated. The spindle is gradually disappearing.
Meaning of mitosis
Due to the unique method of division, each subsequent cell after reproduction has the same composition of genes as its mother. The composition of the chromosomes of both cells receive the same. It did not do without such a science as geometry. Progression in mitosis is important, as all cells reproduce according to this principle.
Where do mutations come from
This process guarantees a constant set of chromosomes and genetic materials in every cell. Due to mitosis, the development of the organism, reproduction, regeneration occurs. In the event of a violation of cell division due to the action of some poisons, the chromosomes may not disperse into their halves, or they may experience structural disturbances. This will be a clear indicator of incipient mutations.
Summing up
What do mathematics and nature have in common? You will find the answer to this question in our article. And if you dig deeper, you needto say that with the help of studying the surrounding world, a person knows himself. Without the Supreme Mind, which gave birth to all living things, nothing could have happened. Nature is exclusively in harmony, in a strict sequence of its laws. Is all this possible without reason?
Let's cite the statement of the scientist, philosopher, mathematician and physicist Henri Poincaré, who, like no one else, will be able to answer the question of whether mathematics is fundamental in nature. Some materialists may not like such reasoning, but they are unlikely to be able to refute it. Poincare says that the harmony that the human mind wants to discover in nature cannot exist outside of it. Objective reality, which is present in the minds of at least a few individuals, can be accessible to all of humanity. The connection that brings together mental activity is called the harmony of the world. Recently, there has been tremendous progress on the way to such a process, but they are very small. These links connecting the Universe and the individual should be valuable to any human mind that is sensitive to these processes.






