The section of physics that studies the features of the movement of liquid media is called hydrodynamics. One of the main mathematical expressions of hydrodynamics is the Bernoulli equation for an ideal fluid. The article is devoted to this topic.
What is an ideal fluid?
Many people know that a liquid substance is such an aggregate state of matter that retains volume under constant external conditions, but changes its shape at the slightest impact on it. An ideal fluid is a fluid substance that has no viscosity and is incompressible. These are the two main properties that distinguish it from real fluids.
Note that almost all real liquids can be considered incompressible, because a small change in their volume requires a huge external pressure. For example, if you create a pressure of 5 atmospheres (500 kPa), then water will increase its density by only 0.024%. As for the issue of viscosity, for a number of practical problems, when water is considered as a working fluid, it can be neglected. For the sake of completeness, we note thatdynamic viscosity of water at 20 oC is 0.001 Pas2, which is meager compared to this value for honey (>2000) value.
It is important not to confuse the concepts of ideal liquid and ideal gas, since the latter is easily compressible.
Continuity equation
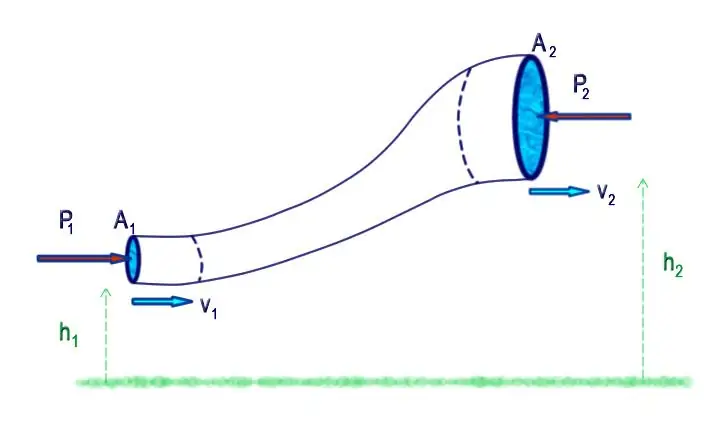
In hydrodynamics, the movement of an ideal fluid begins to be considered from the study of the equation of continuity of its flow. To understand the essence of the issue, it is necessary to consider the movement of fluid through the pipe. Imagine that at the inlet the pipe has a sectional area A1, and at the outlet A2.

Now suppose that the liquid flows at the beginning of the pipe with the speed v1, this means that in time t through the section A1 flow volume V1=A1v1t. Since the liquid is ideal, that is, incompressible, exactly the same volume of water must exit the end of the pipe in time t, we get: V2=A2 v2t. From the equality of the volumes V1 and V2 , the equation for the continuity of the flow of an ideal fluid follows:
A1v1=A2v2.
From the resulting equation it follows that if A1>A2, then v1 should be less than v2. In other words, by reducing the cross section of the pipe, we thereby increase the speed of the fluid flow leaving it. Obviously, this effect was observed by every person in their life who at least once watered flower beds with a hose orgarden, so covering the hole of the hose with your finger, you can watch how the jet of water spouting from it becomes stronger.
Continuity equation for a branched pipe
It is interesting to consider the case of the movement of an ideal fluid through a pipe that has not one, but two or more exits, that is, it is branched. For example, the cross-sectional area of a pipe at the inlet is A1, and towards the outlet it branches into two pipes with sections A2 and A3. Let us determine the flow rates v2 and v3, if it is known that water enters the inlet at a speed v1.
Using the continuity equation, we get the expression: A1v1=A2v 2 + A3v3. To solve this equation for unknown speeds, you need to understand that at the outlet, in whatever pipe the flow is, it moves at the same speed, that is, v2=v 3. This fact can be understood intuitively. If the outlet pipe is divided into two parts by some partition, the flow rate will not change. Given this fact, we get the solution: v2=v3 =A1v 1/(A2 + A3).
Bernoulli's equation for an ideal fluid

Daniil Bernoulli, a Swiss physicist and mathematician of Dutch origin, in his work "Hydrodynamics" (1734) presented an equation for an ideal fluid describing its motion. It is written in the following form:
P+ ρv2/2 + ρgh=const.
This expression reflects the law of conservation of energy in the case of fluid flow. So, the first term (P) is the pressure directed along the fluid displacement vector, which describes the work of the flow, the second term (ρv2/2) is the kinetic energy of the fluid substance, and the third the term (ρgh) is its potential energy.
Recall that this equation is valid for an ideal fluid. In reality, there is always friction of a fluid substance against the walls of the pipe and inside its volume, therefore, an additional term is introduced into the above Bernoulli equation that describes these energy losses.
Using the Bernoulli Equation
It is interesting to cite some inventions that use deductions from the Bernoulli equation:
- Chimney and hoods. It follows from the equation that the greater the speed of movement of a fluid substance, the lower its pressure. The speed of air movement at the top of the chimney is greater than at its base, so the flow of smoke always tends upward due to the pressure difference.
- Water pipes. The equation helps to understand how the water pressure in the pipe will change if the diameter of the latter is changed.
- Airplanes and Formula 1. The angle of the wings of an aircraft and a F1 wing provides a difference in air pressure above and below the wing, which creates lift and down force, respectively.

Modes of fluid flow
Bernoulli's equation is nottakes into account the fluid motion mode, which can be of two types: laminar and turbulent. Laminar flow is characterized by a calm flow, in which fluid layers move along relatively smooth trajectories and do not mix with each other. The turbulent mode of fluid motion is characterized by the chaotic movement of each molecule that makes up the flow. A feature of the turbulent regime is the presence of eddies.

Which way the liquid will flow depends on a number of factors (features of the system, for example, the presence or absence of roughness on the inner surface of the pipe, the viscosity of the substance and the speed of its movement). The transition between the considered modes of motion is described by Reynolds numbers.
A striking example of laminar flow is the slow movement of blood through smooth blood vessels. An example of a turbulent flow is a strong pressure of water from a tap.






