What is the connection between music and exact sciences, like mathematics? People have been asking this question since ancient times. Modern scientists have proven that the mental processes that occur when solving mathematical problems are similar to those that occur during the performance of musical works and the study of subjects of the musical-theoretical cycle.
For example, determining musical intervals by ear is the act of finding the distance between sounds of different pitches. Based on this, it was concluded that the parallel study of music and mathematics can greatly facilitate the assimilation of both sciences.

There is also an obvious similarity between some elements of musical-theoretical and mathematical terminology. This is partly due to the use in both sciences of a number of terms of Latin origin, but nevertheless such a similarity takes place. This article provides definitionsintervals from the point of view of music theory and the answer to the question: what are intervals in mathematics. Also in the article there are examples of the use of the term "interval" in some other areas.
General concept
First, consider the very meaning of the word "interval" and its origin.
So what are intervals?
The word "interval" has Latin roots and can be translated as a gap or a distance. This term, in addition to music and mathematics, is used in such areas of knowledge as: military affairs (indicates the distance between two military personnel, military units, as well as between units of military equipment), medicine (used in cardiography), is of key importance in the theory of relativity, is used in timing floods, volcanic eruptions and similar natural phenomena.
What are intervals in music?
In musical-theoretical disciplines, an interval in the broad sense of the word is the distance between two musical sounds, and in the narrow sense, the consonance of two sounds that can be played simultaneously or sequentially. If the sounds of an interval are taken simultaneously, then such an interval is considered harmonic, and if sequentially, it is melodic.

Musical intervals can be expressed both in mathematical numbers, denoting the number of steps in the interval, and in acoustic units - cents. Intervals have Latin names, according to the number of scale steps contained in them: prima(translated as "first") - one step, a second ("second") - two steps, and so on. They can also be simple and compound. There are eight simple intervals (an octave and all intervals less than it).
Considering the question of what intervals are in music, it is worth mentioning one more value that characterizes them, namely, the number of semitones contained in them. On this basis, the intervals are divided into large and small, clean, reduced and increased.
Other features of musical intervals
Inversion of an interval is the transfer of its lower sound an octave up. At the same time, the qualitative component changes to the opposite - large ones turn into small ones, increased into smaller ones, and so on. Pure intervals always turn only into pure ones. The sum of the numerical designations of consonances converted into each other is nine.

Thus, the prima becomes an octave, the third becomes a sixth, and so on. For compound intervals, the rules are somewhat different: the two sounds of the interval must be moved an octave, the top one an octave up, and the base of the interval an octave down. The sum of the digital designations in this case should be equal to the number sixteen.
The relationship between the two sciences
From the previous information it can be seen that musical-theoretical knowledge is largely based on mathematical calculations. So, the benefit of parallel study of both disciplines is obvious. After all, students of musical educational institutions solve problems in harmony classes, I use all the samearithmetic calculations. With the exception of the happy owners of the so-called "absolute pitch", for whom this work is greatly facilitated by natural abilities.

The benefits of music lessons for the development of mathematical abilities and the development of logical thinking in general were experimentally confirmed by the Hungarian innovative teacher Zoltan Kodaly in the middle of the last century.
He founded several schools with in-depth study of music. Moreover, the number of music lessons was increased by reducing the hours devoted to other subjects. A control cross-section conducted in all subjects at the end of the educational cycle revealed a level of knowledge in students of experimental schools that exceeded the knowledge of students in traditional schools.
What are intervals in mathematics?
In mathematical science, two terms are most often used, denoted by the word "interval". The definitions of these two concepts constitute the answer to the question: what are intervals from the point of view of mathematical science.

So, the most common in mathematics are the intervals of monotonicity and constancy. Consider their definitions.
What are monotonicity intervals?
These are intervals of the value of the function argument, at which the function becomes only increasing or only decreasing.
What are constancy intervals?
These are intervals of the domain of definition at which the sign of the function remains unchanged.
In bothcases we are talking about certain intervals, as in the case of musical intervals.
Perhaps the most striking example of the use of the word "interval" in a specific industry is the well-known computer program "Word". Let's study this moment. What are intervals in Word?
Use in "Word"
It is known that three types of gaps are involved in this program:
- Space between lines.
- Between separate paragraphs.
- Between adjacent pages.
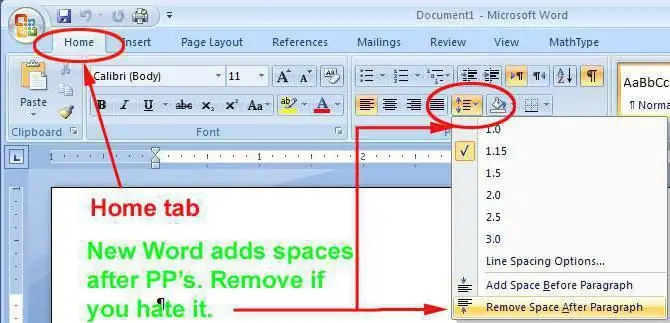
There is no need to consider in detail the meaning of each of the above three intervals used in the Word program, since a lot of literature is devoted to this. It is only worth noting that in this case we are talking about a phenomenon that has, albeit remotely, but similarity with musical intervals.
In closing
This article discussed the relationship between music and mathematics. It was revealed that such a connection really exists, which is proved both by experiments in pedagogical science and by the analysis of thought processes in both types of activity. The question of what intervals are in music and mathematics is also considered. Here, too, some common points in the definitions of mathematical and musical terms are revealed. Now it becomes clear what intervals are. And this once again proves that the area of contact between the two spheres, mathematics and music, really exists.






