The study of the properties of spatial figures plays an important role in solving practical problems. The science that deals with figures in space is called stereometry. In this article, from the point of view of solid geometry, we will consider a cone and show how to find the area of a cone.
Cone with round base
In the general case, a cone is a surface built on some plane curve, all points of which are connected by segments with one point in space. The latter is called the apex of the cone.
From the above definition, it is clear that a curve can have an arbitrary shape, such as parabolic, hyperbolic, elliptical, and so on. Nevertheless, in practice and in problems in geometry, it is often a round cone that is often encountered. It is shown in the picture below.
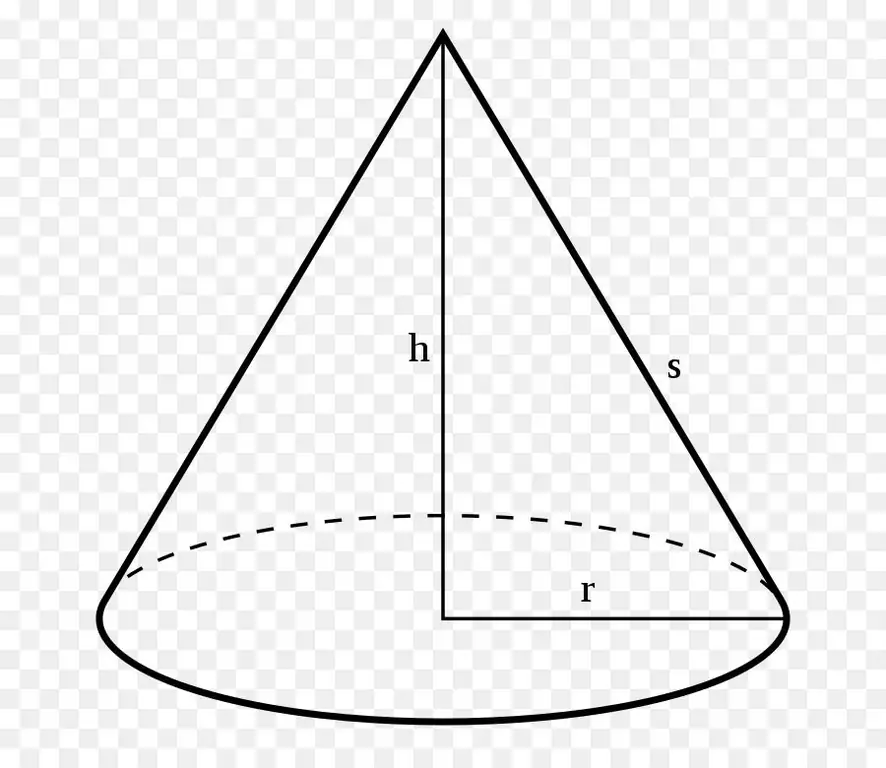
Here the symbol r denotes the radius of the circle located at the base of the figure, h is the perpendicular to the plane of the circle, which is drawn from the top of the figure. It's called height. The value s is the generatrix of the cone, or its generatrix.
It can be seen that the segments r, h and sform a right triangle. If it is rotated around the leg h, then the hypotenuse s will describe the conical surface, and the leg r forms the round base of the figure. For this reason, the cone is considered a figure of revolution. The three named linear parameters are interconnected by the equality:
s2=r2+ h2
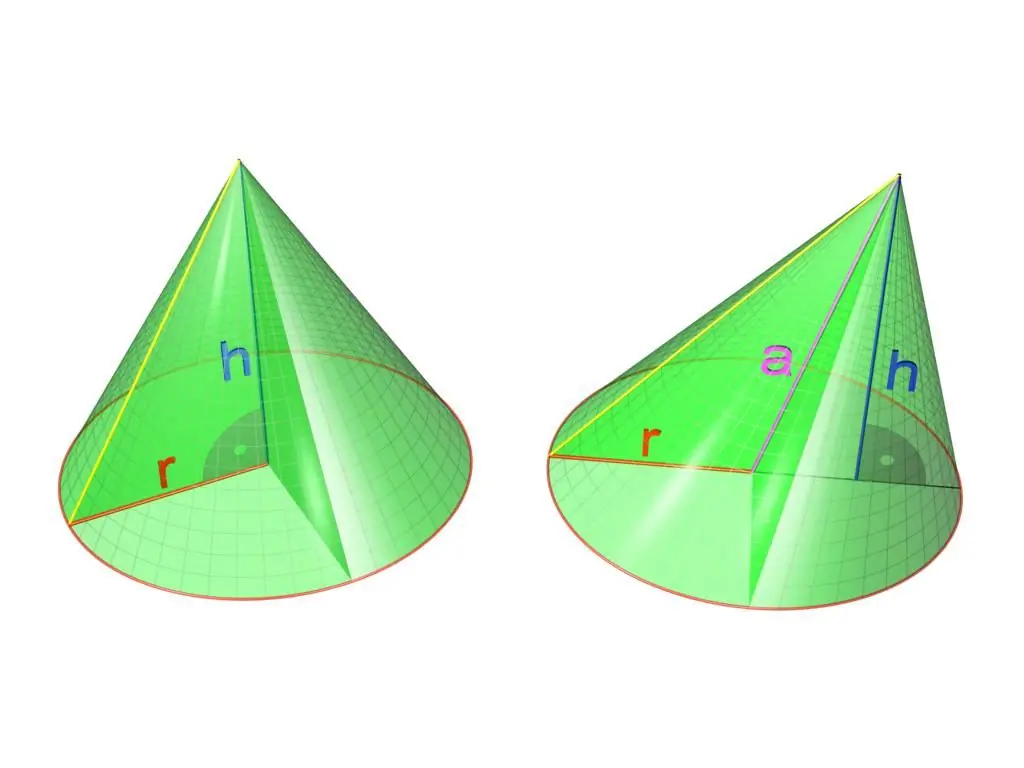
Note that the given equality is valid only for a round straight cone. A straight figure is only if its height falls exactly in the center of the base circle. If this condition is not met, then the figure is called oblique. The difference between straight and oblique cones is shown in the figure below.
Shape development
Studying the surface area of a cone is convenient to carry out, considering it on a plane. This way of representing the surface of figures in space is called their development. For a cone, this development can be obtained as follows: you need to take a figure made, for example, from paper. Then, with scissors, cut off the round base around the circumference. After that, along the generatrix, make a cut of the conical surface and turn it into a plane. The result of these simple operations will be the development of the cone, shown in the figure below.

As you can see, the surface of a cone can indeed be represented on a plane. It consists of the following two parts:
- circle with radius r representing the base of the figure;
- circular sector with radius g, which is a conical surface.
The formula for the area of a cone involves finding the areas of both unfolded surfaces.
Calculate the surface area of a figure
Let's divide the task into two stages. First we find the area of the base of the cone, then the area of the conical surface.
The first part of the problem is easy to solve. Since the radius r is given, it is enough to recall the corresponding expression for the area of a circle to calculate the area of the base. Let's write it down:
So=pi × r2
If the radius is not known, then you should first find it using the relation formula between it, the height and the generator.
The second part of the problem of finding the area of a cone is somewhat more complicated. Note that the circular sector is built on the radius g of the generatrix and is bounded by an arc whose length is equal to the circumference of the circle. This fact allows you to write down the proportion and find the angle of the considered sector. Let's denote it with the Greek letter φ. This angle will be equal to:
2 × pi=>2 × pi × g;
φ=> 2 × pi × r;
φ=2 × pi × r / g
Knowing the central angle φ of a circular sector, you can use the appropriate proportion to find its area. Let's denote it with the symbol Sb. It will be equal to:
2 × pi=>pi × g2;
φ=> Sb;
Sb=pi × g2 × φ / (2 × pi)=pi × r × g
That is, the area of the conical surface corresponds to the product of the generatrix g, the radius of the base r and the number Pi.
Knowing what the areas of bothconsidered surfaces, we can write the final formula for the area of a cone:
S=So+ Sb=pi × r2+ pi × r × g=pi × r × (r + g)
The written expression assumes knowledge of two linear parameters of the cone to calculate S. If g or r is unknown, then they can be found through the height h.
The problem of calculating the area of a cone
It is known that the height of a round straight cone is equal to its diameter. It is necessary to calculate the area of \u200b\u200bthe figure, knowing that the area of \u200b\u200bits base is 50 cm2.
Knowing the area of a circle, you can find the radius of the figure. We have:
So=pi × r2=>
r=√(So /pi)
Now let's find the generator g in terms of h and r. According to the condition, the height h of the figure is equal to two radii r, then:
h=2 × r;
g2=(2 × r)2+ r2=>
g=√5 × r=√(5 × So / pi)
The found formulas for g and r should be substituted into the expression for the entire area of the cone. We get:
S=So+ pi × √(So / pi) × √(5 × S o /pi)=So × (1 + √5)
Into the resulting expression we substitute the area of the base So and write down the answer: S ≈ 161.8 cm2.






