Markov processes were developed by scientists in 1907. Leading mathematicians of that time developed this theory, some of them are still improving it. This system extends to other scientific fields as well. Practical Markov chains are used in various areas where a person needs to arrive in a state of expectation. But in order to clearly understand the system, you need to have knowledge of the terms and provisions. Randomness is considered to be the main factor that determines the Markov process. True, it is not similar to the concept of uncertainty. It has certain conditions and variables.

Features of the randomness factor
This condition is subject to static stability, more precisely, its regularities, which are not taken into account in case of uncertainty. In turn, this criterion allows the use of mathematical methods in the theory of Markov processes, as noted by a scientist who studied the dynamics of probabilities. The work he created de alt directly with these variables. In turn, the studied and developed random process, which has the concepts of state andtransition, as well as used in stochastic and mathematical problems, while allowing these models to function. Among other things, it provides an opportunity to improve other important applied theoretical and practical sciences:
- diffusion theory;
- queuing theory;
- theory of reliability and other things;
- chemistry;
- physics;
- mechanics.
Essential features of an unplanned factor
This Markov process is driven by a random function, that is, any value of the argument is considered to be a given value or one that takes on a pre-prepared form. Examples are:
- oscillations in the circuit;
- moving speed;
- surface roughness in a given area.
It is also commonly believed that time is a fact of a random function, that is, indexing occurs. A classification has the form of a state and an argument. This process can be with discrete as well as continuous states or time. Moreover, the cases are different: everything happens either in one or in another form, or simultaneously.
Detailed analysis of the concept of randomness
It was quite difficult to build a mathematical model with the necessary performance indicators in a clearly analytical form. In the future, it became possible to realize this task, because a Markov random process arose. Analyzing this concept in detail, it is necessary to derive a certain theorem. A Markov process is a physical system that has changed itsposition and condition that has not been pre-programmed. Thus, it turns out that a random process takes place in it. For example: a space orbit and a ship that is launched into it. The result was achieved only due to some inaccuracies and adjustments, without which the specified mode is not implemented. Most of the ongoing processes are inherent in randomness, uncertainty.
On the merits, almost any option that can be considered will be subject to this factor. An airplane, a technical device, a canteen, a clock - all this is subject to random changes. Moreover, this function is inherent in any ongoing process in the real world. However, as long as this does not apply to individually tuned parameters, the disturbances that occur are perceived as deterministic.
The concept of a Markov stochastic process
Designing any technical or mechanical device, device forces the creator to take into account various factors, in particular, uncertainties. The calculation of random fluctuations and perturbations arises at the moment of personal interest, for example, when implementing an autopilot. Some of the processes studied in sciences like physics and mechanics are.
But paying attention to them and conducting rigorous research should begin at the moment when it is directly needed. A Markov random process has the following definition: the probability characteristic of the future form depends on the state in which it is at a given time, and has nothing to do with how the system looked. So giventhe concept indicates that the outcome can be predicted, considering only the probability and forgetting about the background.
Detailed explanation of the concept
At the moment, the system is in a certain state, it is moving and changing, it is basically impossible to predict what will happen next. But, given the probability, we can say that the process will be completed in a certain form or retain the previous one. That is, the future arises from the present, forgetting about the past. When a system or process enters a new state, the history is usually omitted. Probability plays an important role in Markov processes.
For example, the Geiger counter shows the number of particles, which depends on a certain indicator, and not on the exact moment it came. Here the main criterion is the above. In practical application, not only Markov processes can be considered, but also similar ones, for example: aircraft participate in the battle of the system, each of which is indicated by some color. In this case, the main criterion again is the probability. At what point the preponderance in numbers will occur, and for what color, is unknown. That is, this factor depends on the state of the system, and not on the sequence of aircraft deaths.
Structural analysis of processes
A Markov process is any state of a system without a probabilistic consequence and without regard to history. That is, if you include the future in the present and omit the past. Oversaturation of this time with prehistory will lead to multidimensionality andwill display complex constructions of circuits. Therefore, it is better to study these systems with simple circuits with minimal numerical parameters. As a result, these variables are considered determinative and conditioned by some factors.
An example of Markov processes: a working technical device that is in good condition at this moment. In this state of affairs, what is of interest is the likelihood that the device will function for an extended period of time. But if we perceive the equipment as debugged, then this option will no longer belong to the process under consideration due to the fact that there is no information about how long the device worked before and whether repairs were made. However, if these two time variables are supplemented and included in the system, then its state can be attributed to Markov.

Description of discrete state and continuity of time
Markov process models are applied at the moment when it is necessary to neglect the prehistory. For research in practice, discrete, continuous states are most often encountered. Examples of such a situation are: the structure of the equipment includes nodes that can fail during working hours, and this happens as an unplanned, random action. As a result, the state of the system undergoes repair of one or the other element, at this moment one of them will be he althy or both of them will be debugged, or vice versa, they are fully adjusted.
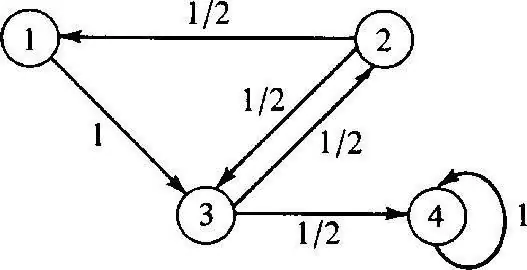
The discrete Markov process is based on probability theory and is alsotransition of the system from one state to another. Moreover, this factor occurs instantly, even if accidental breakdowns and repair work occur. To analyze such a process, it is better to use state graphs, that is, geometric diagrams. System states in this case are indicated by various shapes: triangles, rectangles, dots, arrows.
Modeling of this process
Discrete-state Markov processes are possible modifications of systems as a result of an instantaneous transition, and which can be numbered. For example, you can build a state graph from arrows for nodes, where each will indicate the path of differently directed failure factors, operating state, etc. In the future, any questions may arise: such as the fact that not all geometric elements point in the right direction, because in the process, each node can deteriorate. When working, it is important to consider closures.
Continuous-time Markov process occurs when the data is not pre-fixed, it happens randomly. Transitions were not previously planned and occur in jumps, at any time. In this case, again, the main role is played by probability. However, if the current situation is one of the above, then a mathematical model will be required to describe it, but it is important to understand the theory of possibility.

Probabilistic theories
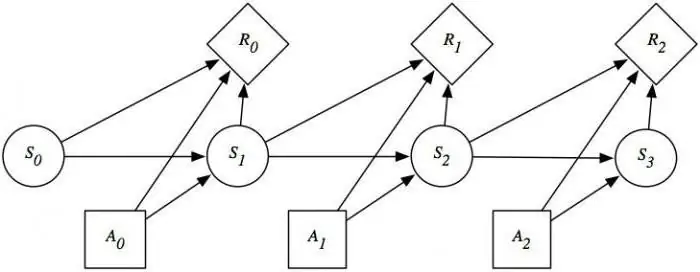
These theories consider probabilistic, having characteristic features likerandom order, movement and factors, mathematical problems, not deterministic, which are certain now and then. A controlled Markov process has and is based on an opportunity factor. Moreover, this system is capable of switching to any state instantly in various conditions and time intervals.
In order to put this theory into practice, it is necessary to have an important knowledge of probability and its application. In most cases, one is in a state of expectation, which in a general sense is the theory in question.
Examples of probability theory
Examples of Markov processes in this situation can be:
- cafe;
- ticket offices;
- repair shops;
- stations for various purposes, etc.
As a rule, people deal with this system every day, today it is called queuing. At facilities where such a service is present, it is possible to demand various requests, which are satisfied in the process.
Hidden process models
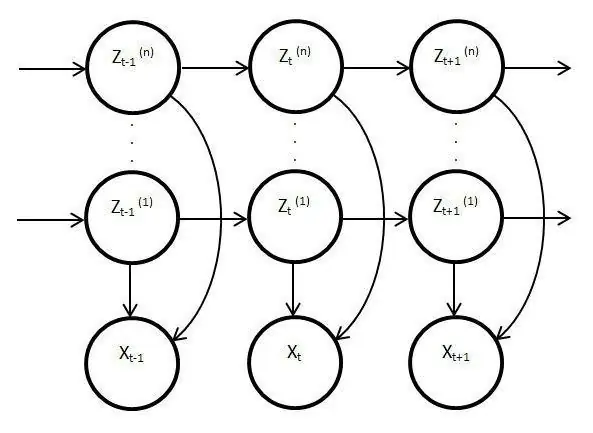
Such models are static and copy the work of the original process. In this case, the main feature is the function of monitoring unknown parameters that must be unraveled. As a result, these elements can be used in analysis, practice, or to recognize various objects. Ordinary Markov processes are based on visible transitions and on probability, only unknowns are observed in the latent modelvariables affected by state.
Essential disclosure of hidden Markov models
It also has a probability distribution among other values, as a result, the researcher will see a sequence of characters and states. Each action has a probability distribution among other values, so the latent model provides information about the generated successive states. The first notes and references to them appeared in the late sixties of the last century.
Then they were used for speech recognition and as analyzers of biological data. In addition, latent models have spread in writing, movements, computer science. Also, these elements imitate the work of the main process and remain static, however, despite this, there are much more distinctive features. In particular, this fact concerns direct observation and sequence generation.
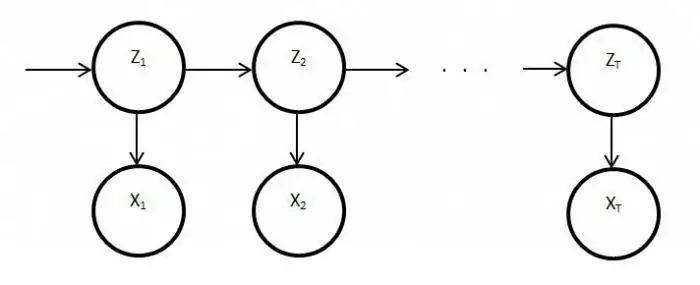
Stationary Markov process
This condition exists for a homogeneous transition function, as well as for a stationary distribution, which is considered the main and, by definition, a random action. The phase space for this process is a finite set, but in this state of affairs, the initial differentiation always exists. Transition probabilities in this process are considered under time conditions or additional elements.
Detailed study of Markov models and processes reveals the issue of satisfying balance in various areas of lifeand activities of the society. Given that this industry affects science and mass services, the situation can be corrected by analyzing and predicting the outcome of any events or actions of the same faulty watches or equipment. To fully use the capabilities of the Markov process, it is worth understanding them in detail. After all, this device has found wide application not only in science, but also in games. This system in its pure form is usually not considered, and if it is used, then only on the basis of the above models and schemes.






