To determine the parallelism and perpendicularity of planes, as well as to calculate the distances between these geometric objects, it is convenient to use one or another type of numerical functions. For what problems is it convenient to use the equation of a plane in segments? In this article, we will look at what it is and how to use it in practical tasks.
What is an equation in line segments?
A plane can be defined in 3D space in several ways. In this article, some of them will be given while solving problems of various types. Here we give a detailed description of the equation in segments of the plane. It generally has the following form:
x/p + y/q + z/r=1.
Where symbols p, q, r denote some specific numbers. This equation can be easily translated into a general expression and into other forms of numerical functions for the plane.
The convenience of writing the equation in segments lies in the fact that it contains the explicit coordinates of the intersection of the plane with perpendicular coordinate axes. On the x-axisrelative to the origin, the plane cuts off a segment of length p, on the y axis - equal to q, on z - of length r.
If any of the three variables is not contained in the equation, then this means that the plane does not pass through the corresponding axis (mathematicians say that it crosses at infinity).
Next, here are some problems in which we will show how to work with this equation.
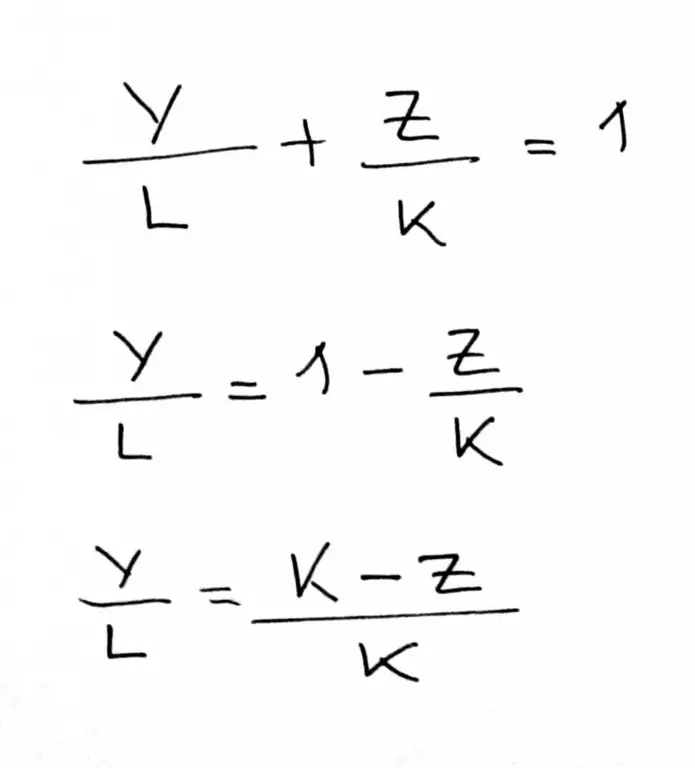
Communication of the general and in segments of equations
It is known that the plane is given by the following equality:
2x - 3y + z - 6=0.
It is necessary to write down this general equation of the plane in segments.
When a similar problem arises, you need to follow this technique: we transfer the free term to the right side of the equality. Then we divide the entire equation by this term, trying to express it in the form given in the previous paragraph. We have:
2x - 3y + z=6=>
2x/6 - 3y/6 + z/6=1=>
x/3 + y/(-2) + z/6=1.
We have obtained in the segments the equation of the plane, given initially in a general form. It is noticeable that the plane cuts off segments with lengths of 3, 2 and 6 for the x, y and z axes, respectively. The y-axis intersects the plane in the negative coordinate area.
When drawing up an equation in segments, it is important that all variables are preceded by a "+" sign. Only in this case, the number by which this variable is divided will show the coordinate cut off on the axis.
Normal vector and point on the plane
It is known that some plane has direction vector (3; 0; -1). It is also known that it passes through the point (1; 1; 1). For this plane, write an equation in segments.
To solve this problem, you should first use the general shape for this two-dimensional geometric object. The general form is written as:
Ax + By + Cz + D=0.
The first three coefficients here are the coordinates of the guide vector, which is specified in the problem statement, that is:
A=3;
B=0;
C=-1.
It remains to find the free term D. It can be determined by the following formula:
D=-1(Ax1+ By1+ Cz1).
Where the coordinate values with index 1 correspond to the coordinates of a point belonging to the plane. We substitute their values from the condition of the problem, we get:
D=-1(31 + 01 + (-1)1)=-2.
Now you can write the full equation:
3x - z - 2=0.
The technique for converting this expression into an equation in segments of the plane has already been demonstrated above. Apply it:
3x - z=2=>
x/(2/3) + z/(-2)=1.
The answer to the problem has been received. Note that this plane only intersects the x and z axes. For y it is parallel.
Two straight lines defining a plane
From the course of spatial geometry, every student knows that two arbitrary lines uniquely define a plane inthree-dimensional space. Let's solve a similar problem.
Two equations of lines are known:
(x; y; z)=(1; 0; 0) + α(2; -1; 0);
(x; y; z)=(1; -1; 0) + β(-1; 0; 1).
It is necessary to write down the equation of the plane in segments, passing through these lines.
Since both lines must lie in the plane, this means that their vectors (guides) must be perpendicular to the vector (guide) for the plane. At the same time, it is known that the vector product of arbitrary two directed segments gives the result in the form of coordinates of the third, perpendicular to the two original ones. Given this property, we obtain the coordinates of a vector normal to the desired plane:
[(2; -1; 0)(-1; 0; 1)]=(-1; -2; -1).
Since it can be multiplied by an arbitrary number, this forms a new directed segment parallel to the original one, we can replace the sign of the obtained coordinates with the opposite (multiply by -1), we get:
(1; 2; 1).
We know the direction vector. It remains to take an arbitrary point of one of the straight lines and draw up the general equation of the plane:
A=1;
B=2;
C=1;
D=-1(11 + 20 + 30)=-1;
x + 2y + z -1=0.
Translating this equality into an expression in segments, we get:
x + 2y + z=1=>
x/1 + y/(1/2) + z/1=1.
Thus, the plane intersects all three axes in the positive region of the coordinate system.
Three points and a plane
Just like two straight lines, three points define a plane uniquely in three-dimensional space. We write the corresponding equation in segments if the following coordinates of points lying in the plane are known:
Q(1;-2;0);
P(2;-3;0);
M(4; 1; 0).
Let's do the following: calculate the coordinates of two arbitrary vectors connecting these points, then find the vector n¯ normal to the plane by calculating the product of the found directed segments. We get:
QP¯=P - Q=(1; -1; 0);
QM¯=M - Q=(2; 4; 0);
n¯=[QP¯QM¯]=[(1; -1; 0)(2; 4; 0)]=(0; 0; 6).
Take the point P as an example, compose the equation of the plane:
A=0;
B=0;
C=6;
D=-1(02 + 0(-3) + 60)=0;
6z=0 or z=0.
We have obtained a simple expression that corresponds to the xy plane in the given rectangular coordinate system. It cannot be written in segments, since the x and y axes belong to the plane, and the length of the segment cut off on the z axis is zero (the point (0; 0; 0) belongs to the plane).






