The world that surrounds us is in constant motion. Nevertheless, there are systems that can be in a relative state of rest and equilibrium. One of them is the lever. In this article, we will consider what it is from the point of view of physics, and also solve a couple of problems on the balance condition of the lever.
What is a lever?
In physics, a lever is a simple mechanism consisting of a weightless beam (board) and one support. The location of the support is not fixed, so it can be located closer to one of the ends of the beam.
Being a simple mechanism, the lever serves to convert force into a path, and vice versa. Despite the fact that force and path are completely different physical quantities, they are related to each other by the work formula. To lift any load, you need to do some work. This can be done in two different ways: apply a large force and move the load a short distance, or act with a small force, but at the same time increase the distance of movement. Actually, this is what leverage is for. In short, this mechanism allows you to win on the road and lose in strength, or, conversely, win in strength, but lose on the road.

Forces acting on the lever
This article is devoted to the equilibrium conditions of the lever. Any equilibrium in statics (a branch of physics that studies bodies at rest) presupposes the presence or absence of forces. If we consider the lever in free form (weightless beam and support), then no forces act on it, and it will be in balance.
When work is done with a lever of any type, there are always three forces acting on it. Let's list them:
- Cargo weight. Since the mechanism in question is used to lift loads, it is obvious that their weight will have to be overcome.
- External reaction force. This is the force applied by a person or other machine to counteract the weight of the load on the arm beam.
- Reaction of the support. The direction of this force is always perpendicular to the plane of the lever beam. The reaction force of the support is directed upwards.
The equilibrium condition of the lever involves considering not so much the marked acting forces as the moments of forces created by them.
What is moment of force
In physics, the moment of force, or torque, is called a value equal to the product of an external force by a shoulder. The shoulder of force is the distance from the point of application of the force to the axis of rotation. The presence of the latter is important in calculating the moment of force. Without the presence of an axis of rotation, there is no point in talking about the moment of force. Given the above definition, we can write the following expression for the torque M:
M=Fd
In fairness, we note that the moment of force is actually a vector quantity, however, to understand the topic of this article, it is enough to know how the modulus of the moment of force is calculated.
Besides the formula above, it should be remembered that if the force F tends to rotate the system so that it begins to move counterclockwise, then the moment created is considered positive. Conversely, the tendency to rotate the system in the direction of the clock indicates a negative torque.
Formula for the equilibrium condition of the lever
The figure below shows a typical lever, and the values of its right and left shoulders are also marked. The external force is labeled F and the weight to be lifted is labeled R.
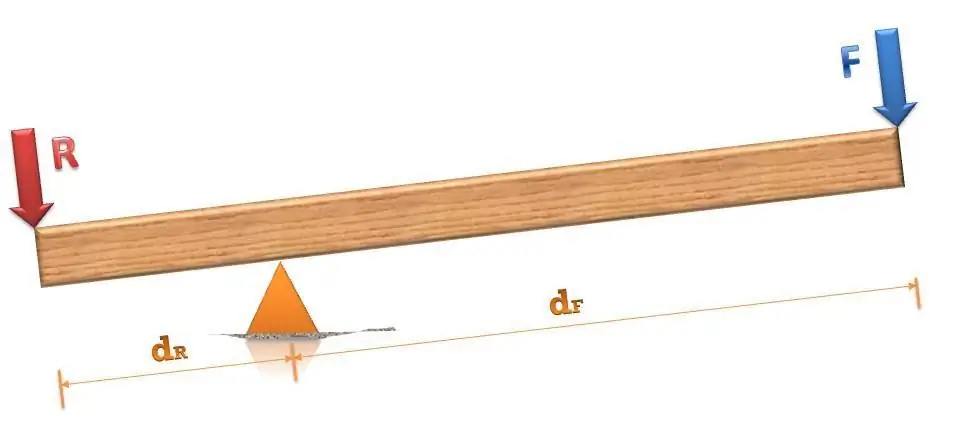
In statics, in order for the system to rest, two conditions must be met:
- The sum of external forces that affect the system must be equal to zero.
- The sum of all the moments of the mentioned forces about any axis must be zero.
The first of these conditions means the absence of a translational movement of the system. It is obvious to the lever, since its support is firmly on the floor or ground. Therefore, checking the equilibrium condition of the lever involves only checking the validity of the following expression:
∑i=1Mi=0
Because in our caseonly three forces act, rewrite this formula as follows:
RdR- FdF+ N0=0
The reaction force of the moment support does not create. Let's rewrite the last expression as follows:
RdR=FdF
This is the equilibrium condition of the lever (it is studied in the 7th grade of secondary schools in the course of physics). The formula shows: if the value of the force F is greater than the weight of the load R, then the shoulder dFshould be less than the shoulder dR. The latter means that by applying a large force over a short distance, we can move the load over a long distance. The reverse situation is also true, when F<R and, accordingly, dF>dR. In this case, the gain is observed in force.
Elephant and Ant Problem
Many people know the famous saying of Archimedes about the possibility of using a lever to move the entire globe. This bold statement makes physical sense, given the lever equilibrium formula written above. Let's leave Archimedes and the Earth alone and solve a slightly different problem, which is no less interesting.
The elephant and the ant were placed on different arms of the lever. Suppose the elephant's center of mass is one meter from the support. How far from the support must the ant be to balance the elephant?
To answer the question of the problem, let's turn to the tabular data on the masses of the considered animals. Let's take the mass of an ant as 5 mg (510-6kg), the mass of an elephant will be considered equal to 5000 kg. Using the lever balance formula, we get:
50001=510-6x=>
x=5000/(510-6)=109m.
An ant can indeed balance an elephant, but to do this, it must be located at a distance of 1 million kilometers from the lever support, which corresponds to 1/150 of the distance from the Earth to the Sun!
Problem with support at the end of a beam
As noted above, at the lever, the support under the beam can be located anywhere. Assume that it is located near one of the ends of the beam. Such a lever has a single arm, shown in the figure below.

Assume that the load (red arrow) has a mass of 50 kg and is located exactly in the middle of the lever arm. How much external force F (blue arrow) must be applied to the end of the arm to balance this weight?
Let's designate the length of the lever arm as d. Then we can write the equilibrium condition in the following form:
Fd=Rd/2=>
F=mg/2=509, 81/2=245, 25 N
Thus, the magnitude of the applied force must be half the weight of the load.

This type of lever is used in inventions such as the hand wheelbarrow or the nutcracker.






