The section of physics that studies bodies at rest from the point of view of mechanics is called statics. The key points of statics are the understanding of the equilibrium conditions of bodies in the system and the ability to apply these conditions to solve practical problems.
Acting forces
The reason for the rotation, translational movement or complex movement of bodies along curved trajectories is the action of an external non-zero force on these bodies. In physics, a force is a quantity that, acting on a body, is able to give it acceleration, that is, change the amount of motion. This value has been studied since ancient times, however, the laws of statics and dynamics finally took shape in a coherent physical theory only with the advent of new times. A major role in the development of the mechanics of motion was played by the work of Isaac Newton, after whom the unit of force is now called the Newton.
When considering the equilibrium conditions of bodies in physics, it is important to know several parameters of the acting forces. These include the following:
- direction of action;
- absolute value;
- application point;
- angle between the considered force and other forces applied to the system.
The combination of the above parameters makes it possible to unambiguously say whether the given system will move or be at rest.
The first equilibrium condition of the system
When will a system of rigid bodies not move progressively in space? The answer to this question will become clear if we recall Newton's second law. According to him, the system will not perform translational movement if and only if the sum of forces external to the system is equal to zero. That is, the first equilibrium condition for solids mathematically looks like this:
∑i=1Fi¯=0.
Here n is the number of external forces in the system. The above expression assumes the vector summation of forces.
Let's consider a simple case. Let us assume that two forces of the same magnitude act on the body, but directed in different directions. As a result, one of them will tend to give acceleration to the body along the positive direction of an arbitrarily chosen axis, and the other - along the negative one. The result of their action will be a body at rest. The vector sum of these two forces will be zero. In fairness, we note that the described example will lead to the appearance of tensile stresses in the body, but this fact does not apply to the topic of the article.
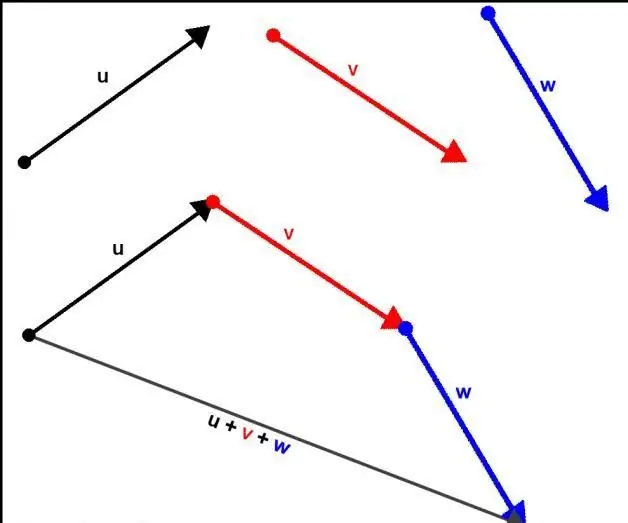
To facilitate the verification of the written equilibrium condition of bodies, you can use the geometric representation of all forces in the system. If their vectors are arranged so that each subsequent force starts from the end of the previous one,then the written equality will be fulfilled when the beginning of the first force coincides with the end of the last one. Geometrically, this looks like a closed loop of force vectors.
Moment of force
Before proceeding to the description of the next equilibrium condition for a rigid body, it is necessary to introduce an important physical concept of statics - the moment of force. In simple terms, the scalar value of the moment of force is the product of the modulus of the force itself and the radius vector from the axis of rotation to the point of application of the force. In other words, it makes sense to consider the moment of force only relative to some axis of rotation of the system. The scalar mathematical form of writing the moment of force looks like this:
M=Fd.
Where d is the arm of the force.
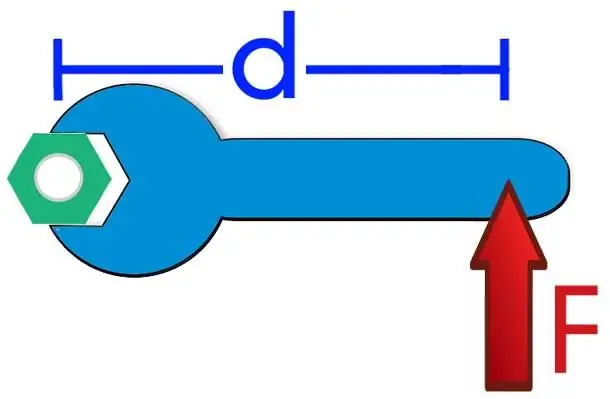
From the written expression it follows that if the force F is applied to any point of the axis of rotation at any angle to it, then its moment of force will be equal to zero.
The physical meaning of the quantity M lies in the ability of the force F to make a turn. This ability increases as the distance between the point of application of the force and the axis of rotation increases.
Second equilibrium condition for the system
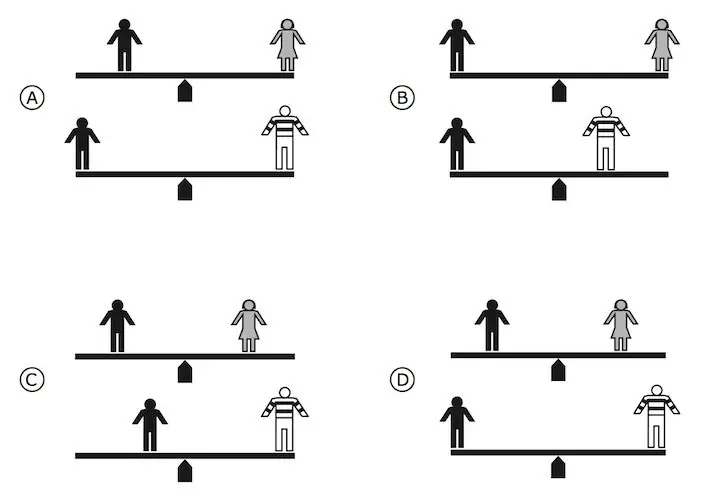
As you might guess, the second condition for the equilibrium of bodies is connected with the moment of force. First, we give the corresponding mathematical formula, and then we will analyze it in more detail. So, the condition for the absence of rotation in the system is written as follows:
∑i=1Mi=0.
That is, the sum of the moments of allforces must be zero about each axis of rotation in the system.
The moment of force is a vector quantity, but to determine the rotational equilibrium it is important to know only the sign of this moment Mi. It should be remembered that if the force tends to rotate in the direction of the clock, then it creates a negative moment. On the contrary, rotation against the direction of the arrow leads to the appearance of a positive moment Mi.
Method of determining the equilibrium of the system

Two conditions for the equilibrium of bodies were given above. Obviously, in order for the body to not move and be at rest, both conditions must be met simultaneously.
When solving equilibrium problems, one should consider a system of written two equations. The solution of this system will give an answer to any problem in statics.
Sometimes the first condition, reflecting the absence of translational motion, may not provide any useful information, then the solution of the problem is reduced to the analysis of the moment condition.
When considering the problems of statics on the equilibrium conditions of bodies, the center of gravity of the body plays an important role, since it is through it that the axis of rotation passes. If the sum of the moments of forces relative to the center of gravity is equal to zero, then the rotation of the system will not be observed.
Example of problem solving
It is known that two weights were put on the ends of a weightless board. The weight of the right weight is twice as much as the weight of the left one. It is necessary to determine the position of the support under the board, in which this system would be inbalance.

Design the length of the board with the letter l, and the distance from its left end to the support - with the letter x. It is clear that this system does not experience any translational motion, so the first condition does not need to be applied to solve the problem.
The weight of each load creates a moment of force relative to the support, and both moments have a different sign. In the notation we have chosen, the second equilibrium condition will look like:
P1x=P2(L-x).
Here P1 and P2 are the weights of the left and right weights, respectively. Dividing by P1both parts of the equality, and using the condition of the problem, we get:
x=P2/P1(L-x)=>
x=2L - 2x=>
x=2/3L.
So that the system is in balance, the support should be located 2/3 of the length of the board from its left end (1/3 from the right end).






