Circular motion or rotational movement of solids is one of the important processes that are studied by the branches of physics - dynamics and kinematics. We will devote this article to considering the question of how the angular acceleration that appears during the rotation of bodies is measured.
The concept of angular acceleration
Obviously, before giving an answer to the question of how angular acceleration is measured in physics, one should get acquainted with the concept itself.
In the mechanics of linear motion, acceleration plays the role of a measure of the rate of change of speed and is introduced into physics through Newton's second law. In the case of rotational motion, there is a quantity similar to linear acceleration, which is called angular acceleration. The formula for determining it is written as:
α=dω/dt.
That is, the angular acceleration α is the first derivative of the angular velocity ω with respect to time. So, if the speed does not change during rotation, then the acceleration will be zero. If the speed depends linearly on time, for example, it increases constantly, then the acceleration α will take on a constant non-zero positive value. A negative value of α indicates that the system is slowing down.
Rotation dynamics
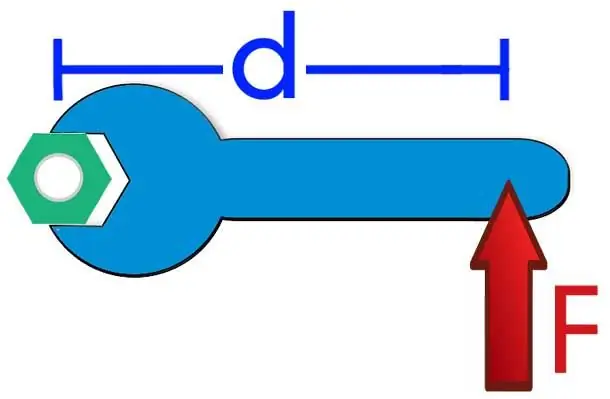
In physics, any acceleration occurs only when there is a non-zero external force acting on the body. In the case of rotational movement, this force is replaced by a moment of force M, equal to the product of the arm d and the modulus of force F. The well-known equation for the moments of the dynamics of the rotational movement of bodies is written as follows:
M=αI.
Here I is the moment of inertia, which plays the same role in the system as the mass during linear movement. This formula allows you to calculate the value of α, as well as determine what the angular acceleration is measured in. We have:
α=M/I=[Nm/(kgm2)]=[N/(kgm)].
We got the unit α from the moment equation, however, the newton is not the base SI unit, so it should be replaced. To accomplish this task, we use Newton's second law, we get:
1 N=1 kgm/s2;
α=1 [N/(kgm)]=1 kgm/s2/(kgm)=1 [1/s 2].
We have received an answer to the question in what units the angular acceleration is measured. It is measured in reciprocal square seconds. The second, unlike the newton, is one of the seven basic SI units, so the resulting unit for α is used in mathematical calculations.
The resulting unit of measurement for angular acceleration is correct, however, it is difficult to understand the physical meaning of the quantity from it. In this regard, the problem posed can be solved in a different way, using the physical definition of acceleration, which was written in the previous paragraph.
Angular velocity and acceleration
Let's get back to the definition of angular acceleration. In the kinematics of rotation, the angular velocity determines the angle of rotation per unit time. Angle units can be either degrees or radians. The latter are more commonly used. Thus, angular velocity is measured in radians per second or rad/s for short.
Since angular acceleration is the time derivative of ω, to get its units of measurement, it is enough to divide the unit for ω by a second. The latter means that the value of α will be measured in radians per square second (rad/s2). So, 1 rad/s2means that for every second of rotation the angular velocity will increase by 1 rad/s.
The unit under consideration for α is similar to that obtained in the previous paragraph of the article, where the value of radians was omitted, since it is implied in accordance with the physical meaning of angular acceleration.
Angular and centripetal accelerations

Having answered the question of what angular acceleration is measured in (the formulas are given in the article), it is also useful to understand how it is related to centripetal acceleration, which is an integral characteristicany rotation. The answer to this question sounds simple: angular and centripetal accelerations are completely different quantities that are independent.
Centripetal acceleration provides only a curvature of the body's trajectory during rotation, while angular acceleration leads to a change in linear and angular velocities. So, in the case of uniform motion along a circle, the angular acceleration is zero, while the centripetal acceleration has some constant positive value.
Angular acceleration α is related to linear tangential acceleration a by the following formula:
α=a/r.
Where r is the radius of the circle. By substituting the units for a and r into this expression, we also get the answer to the question of what angular acceleration is measured in.
Problem Solving
Let's solve the following problem from physics. A force of 15 N tangent to the circle acts on a material point. Knowing that this point has a mass of 3 kg and rotates around an axis with a radius of 2 meters, it is necessary to determine its angular acceleration.
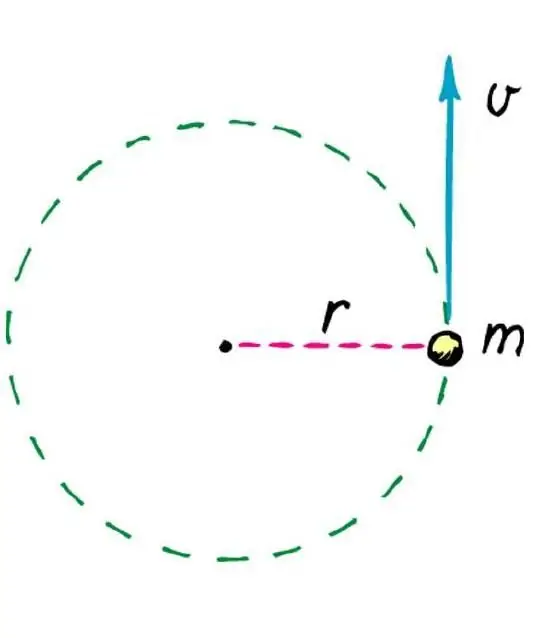
This problem is solved using the equation of moments. The moment of force in this case is:
M=Fr=152=30 Nm.
The moment of inertia of a point is calculated using the following formula:
I=mr2=322=12kgm2.
Then the acceleration value will be:
α=M/I=30/12=2.5 rad/s2.
Thus, for every second of movement of a material point, the speed of its rotationwill increase by 2.5 radians per second.






