The rotation of bodies is one of the important types of mechanical movement in technology and nature. Unlike linear movement, it is described by its own set of kinematic characteristics. One of them is angular acceleration. We characterize this value in the article.
Rotation movement
Before talking about angular acceleration, let's describe the type of motion it applies to. We are talking about rotation, which is the movement of bodies along circular paths. For rotation to occur, certain conditions must be met:
- presence of an axis or point of rotation;
- the presence of a centripetal force that would keep the body in a circular orbit.
Examples of this type of movement are various attractions, such as a carousel. In engineering, rotation manifests itself in the movement of wheels and shafts. In nature, the most striking example of this type of motion is the rotation of the planets around their own axis and around the Sun. The role of the centripetal force in these examples is played by the forces of interatomic interaction in solids and the gravitationalinteraction.

Kinematic characteristics of rotation
These characteristics include three quantities: angular acceleration, angular velocity and angle of rotation. We will denote them by the Greek symbols α, ω and θ, respectively.
Since the body is moving in a circle, it is convenient to calculate the angle θ, which it will turn in a certain time. This angle is expressed in radians (rarely in degrees). Since the circle has 2 × pi radians, we can write an equation relating θ to the arc length L of the turn:
L=θ × r
Where r is the radius of rotation. This formula is easy to obtain if you remember the corresponding expression for the circumference.
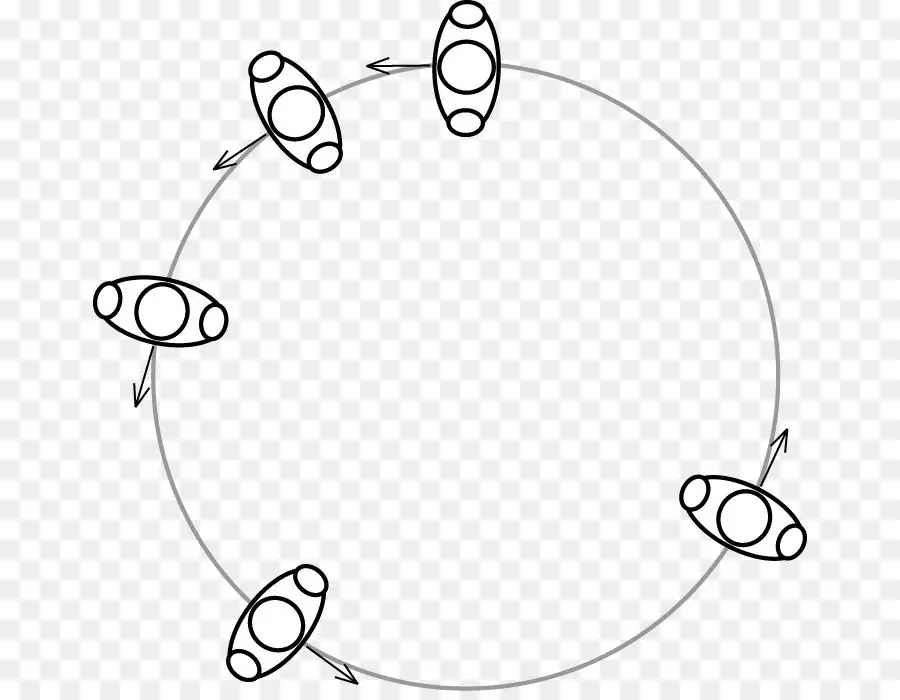
Angular velocity ω, like its linear counterpart, describes the speed of rotation around the axis, that is, it is determined according to the following expression:
ω¯=d θ / d t
The quantity ω¯ is a vector value. It is directed along the axis of rotation. Its unit is radians per second (rad/s).
Finally, angular acceleration is a physical characteristic that determines the rate of change in the value of ω¯, which is mathematically written as follows:
α¯=d ω¯/ d t
Vector α¯ is directed towards changing the velocity vector ω¯. Further it will be said that the angular acceleration is directed towards the vector of the moment of force. This value is measured in radians.square second (rad/s2).
Moment of force and acceleration
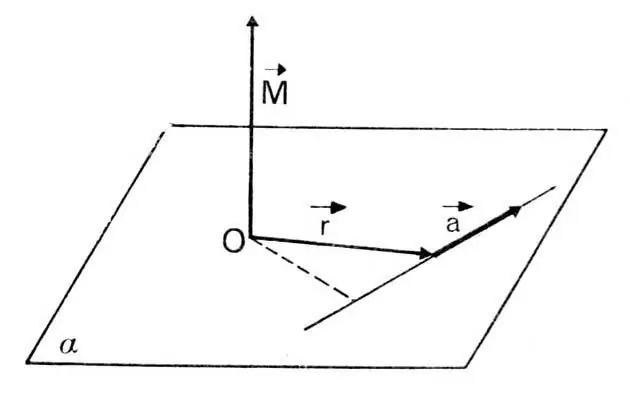
If we recall Newton's law, which connects force and linear acceleration into a single equality, then, transferring this law to the case of rotation, we can write the following expression:
M¯=I × α¯
Here M¯ is the moment of force, which is the product of the force that tends to spin the system times the lever - the distance from the point of force application to the axis. The value I is analogous to the mass of the body and is called the moment of inertia. The written formula is called the equation of moments. From it, the angular acceleration can be calculated as follows:
α¯=M¯/ I
Since I is a scalar, α¯ is always directed towards the acting moment of force M¯. The direction of M¯ is determined by the right hand rule or the gimlet rule. The vectors M¯ and α¯ are perpendicular to the plane of rotation. The greater the moment of inertia of the body, the lower the value of the angular acceleration that the fixed moment M¯ can impart to the system.
Kinematic equations
To understand the important role that angular acceleration plays in describing the motion of rotation, let's write down the formulas connecting the kinematic quantities studied above.
In the case of uniformly accelerated rotation, the following mathematical relationships are valid:
ω=α × t;
θ=α × t2 / 2
The first formula shows that the angularthe speed will increase in time according to a linear law. The second expression allows you to calculate the angle by which the body will turn in a known time t. The graph of the function θ(t) is a parabola. In both cases, the angular acceleration is a constant.
If we use the relation formula between L and θ given at the beginning of the article, we can get an expression for α in terms of linear acceleration a:
α=a / r
If α is constant, then as the distance from the axis of rotation r increases, the linear acceleration a will increase proportionally. That is why angular characteristics are used for rotation, unlike linear ones, they do not change with increasing or decreasing r.
Example problem
The metal shaft, rotating at a frequency of 2,000 revolutions per second, began to slow down and stopped completely after 1 minute. It is necessary to calculate with what angular acceleration the process of deceleration of the shaft took place. You should also calculate the number of revolutions that the shaft made before stopping.
The process of rotation deceleration is described by the following expression:
ω=ω0- α × t
The initial angular velocity ω0is determined from the rotation frequency f as follows:
ω0=2 × pi × f
Since we know the deceleration time, then we get the acceleration value α:
α=ω0 / t=2 × pi × f / t=209.33 rad/s2
This number should be taken with a minus sign,because we are talking about slowing down the system, not speeding it up.
To determine the number of revolutions that the shaft will make during braking, apply the expression:
θ=ω0 × t - α × t2 / 2=376,806 rad.
The obtained value of the angle of rotation θ in radians is simply converted into the number of revolutions made by the shaft before it comes to a complete stop using a simple division by 2 × pi:
n=θ / (2 × pi)=60,001 turns.
Thus, we got all the answers to the questions of the problem: α=-209, 33 rad/s2, n=60,001 revolutions.






