When studying in physics the mechanical motion of bodies in space, they always take into account the resulting acceleration. Let's consider in the article what acceleration is, and how it is denoted in physics, and also solve a simple problem to calculate this value.
What is acceleration and what are its types?
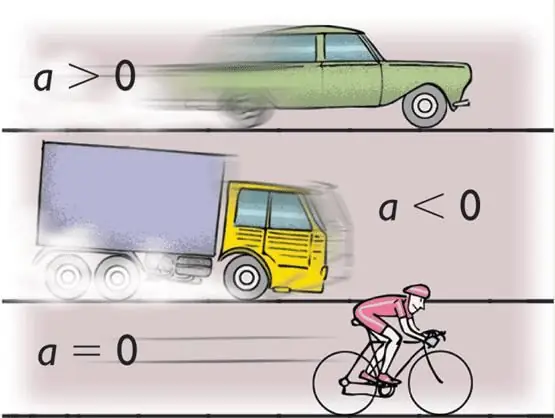
Under the acceleration understand the value, the meaning of which is the speed of change in the speed of the body. Mathematically, this definition is written as follows:
a=dv/dt.
If the time function of speed is known, then it is enough to find its first derivative in order to calculate the acceleration at a given time.
In physics, the letter of acceleration is the lowercase Latin a. However, this is the so-called linear acceleration, which is measured in units of m/s2. In addition to it, there is also angular acceleration. It shows the change in angular velocity and is expressed in units of rad/s2. This type of acceleration is denoted by the Greek lowercase letter α (alpha). Sometimesthe letter ε (epsilon) is used to denote it.
If the body moves along a curved trajectory, then the total acceleration is decomposed into two components: tangential (determining the change in speed in magnitude) and normal (determining the change in speed in direction). These types of acceleration are also denoted by the letters a, but using the corresponding indices: at and a. Normal is often called centripetal, and tangential is often called tangent.
Finally, there is another type of acceleration that occurs when bodies fall freely in the planet's gravitational field. It is denoted by the letter g.
Problem in physics for acceleration
It is known that the body moves in a straight line. Its speed over time is determined by the following law:
v=2t2-t+4.
It is necessary to calculate the acceleration that the body will have at time t=2.5 seconds.
Following the definition of a, we get:
a=dv/dt=4t - 1.
That is, the value a depends linearly on time. It is curious to note that at the initial moment (t=0) the acceleration was negative, that is, directed against the velocity vector. We get the answer to the problem by substituting t=2.5 seconds into this equation: a=9 m/s2.






