Movement is a physical process that involves changing the spatial coordinates of the body. To describe motion in physics, special quantities and concepts are used, the main of which is acceleration. In this article, we will study the question that this is normal acceleration.
General definition
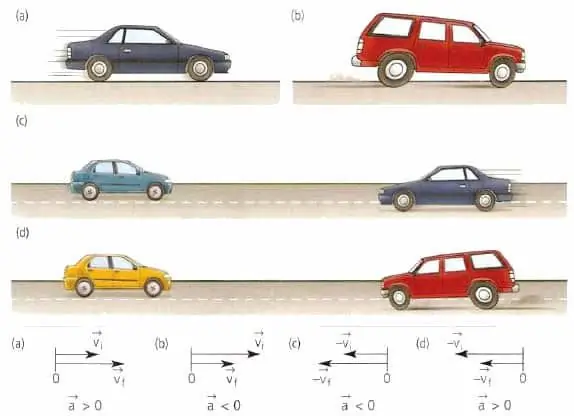
Under the acceleration in physics understand the speed of change of speed. Velocity itself is a vector kinematic characteristic. Therefore, the definition of acceleration means not only a change in the absolute value, but also a change in the direction of the speed. What does the formula look like? For full acceleration a¯ it is written as follows:
a¯=dv¯/dt
That is, to calculate the value of a¯, it is necessary to find the derivative of the velocity vector with respect to time at a given moment. The formula shows that a¯ is measured in meters per second squared (m/s2).
The direction of full acceleration a¯ has nothing to do with the vector v¯. However, it matcheswith vector dv¯.
The reason for the appearance of acceleration in moving bodies is an external force of any nature acting on them. Acceleration never occurs if the external force is zero. The direction of the force is the same as the direction of acceleration a¯.
Curvilinear path
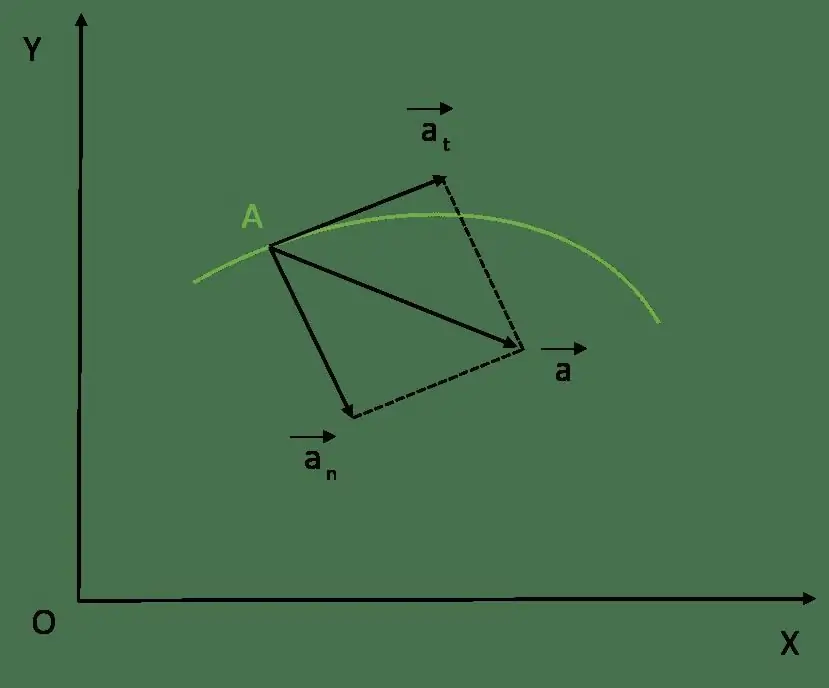
In the general case, the considered quantity a¯ has two components: normal and tangential. But first of all, let us recall what a trajectory is. In physics, a trajectory is understood as a line along which a body passes a certain path in the process of motion. Since the trajectory can be either a straight line or a curve, the movement of bodies is divided into two types:
- rectilinear;
- curvilinear.
In the first case, the body's velocity vector can only change to the opposite. In the second case, the velocity vector and its absolute value change constantly.
As you know, the speed is directed tangentially to the trajectory. This fact allows us to enter the following formula:
v¯=vu¯
Here u¯ is the unit tangent vector. Then the expression for full acceleration will be written as:
a¯=dv¯/dt=d(vu¯)/dt=dv/dtu¯ + vdu¯/dt.
When obtaining equality, we used the rule for calculating the derivative of the product of functions. Thus, the total acceleration a¯ is represented as the sum of two components. The first is its tangent component. In this article, shenot considered. We only note that it characterizes the change in the modulus of velocity v¯. The second term is the normal acceleration. About him below in the article.
Normal point acceleration
Design this acceleration component as a¯. Let's write the expression for it again:
a¯=vdu¯/dt
Normal acceleration equation a¯ can be written explicitly if the following mathematical transformations are carried out:
a¯=vdu¯/dt=vdu¯/d l dl/dt=v2/rre¯.
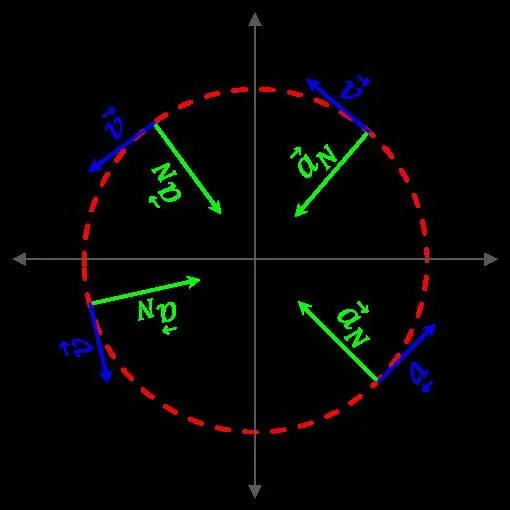
Here l is the path traveled by the body, r is the radius of curvature of the trajectory, re¯ is the unit radius vector directed towards the center of curvature. This equality allows us to draw some important conclusions regarding the question that this is a normal acceleration. Firstly, it does not depend on the change in the velocity modulus and is proportional to the absolute value of v¯; secondly, it is directed towards the center of curvature, that is, along the normal to the tangent at a given point of the trajectory. That is why the component a¯ is called normal or centripetal acceleration. Finally, thirdly, a ¯ is inversely proportional to the radius of curvature r, which everyone experienced experimentally on themselves when they were a passenger in a car entering a long and sharp turn.
Centripetal and centrifugal forces
It was noted above that the cause of anyacceleration is a force. Since the normal acceleration is the component of the total acceleration that is directed towards the center of curvature of the trajectory, there must be some centripetal force. Its nature is easiest to follow through various examples:
- Unwinding a stone tied to the end of a rope. In this case, the centripetal force is the tension in the rope.
- Long turn of the car. Centripetal is the friction force of car tires on the road surface.
- Rotation of the planets around the Sun. Gravitational attraction plays the role of the force in question.
In all these examples, the centripetal force leads to a change in the rectilinear trajectory. In turn, it is prevented by the inertial properties of the body. They are associated with centrifugal force. This force, acting on the body, tries to "throw" it out of the curvilinear trajectory. For example, when a car makes a turn, passengers are pressed against one of the vehicle's doors. This is the action of centrifugal force. It, unlike centripetal, is fictitious.
Example problem
As you know, our Earth revolves in a circular orbit around the Sun. It is necessary to determine the normal acceleration of the blue planet.

To solve the problem, we use the formula:
a=v2/r.
From the reference data we find that the linear velocity v of our planet is 29.78 km/s. The distance r to our star is 149,597,871 km. Translating thesenumbers in meters per second and meters, respectively, substituting them into the formula, we get the answer: a=0.006 m/s2, which is 0, 06% of the planet's gravitational acceleration.






