Tangential and normal acceleration. Tangent and normal acceleration

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

The study of physics begins with the consideration of mechanical motion. In the general case, bodies move along curved trajectories with variable velocities. To describe them, the concept of acceleration is used. In this article, we will consider what tangential and normal acceleration are.

Kinematic quantities. Velocity and acceleration in physics

Kinematics of mechanical motion is a branch of physics that studies and describes the movement of bodies in space. Kinematics operates with three main quantities:

• traversed path;
• speed;
• acceleration.

In the case of movement along a circle, similar kinematic characteristics are used, which are reduced to the central angle of the circle.

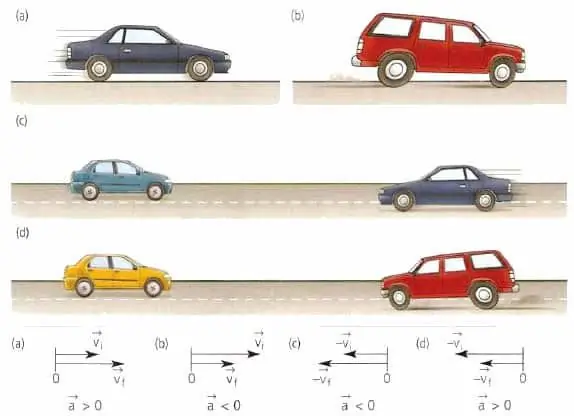
Everyone is familiar with the concept of speed. It shows the rate of change in the coordinates of bodies in motion. The speed is always directed tangentially to the line along which the body moves (trajectories). Further, the linear velocity will be denoted by v¯, and the angular velocity by ω¯.

Acceleration is the rate of change of v¯ and ω¯. Acceleration is also a vector quantity, but its direction is completely independent of the velocity vector. Acceleration is always directed towards the force acting on the body, which causes a change in the velocity vector. Acceleration for any type of movement can be calculated using the formula:

a¯=dv¯ / dt

The more the speed changes over the time interval dt, the greater will be the acceleration.

To understand the information presented below, it must be remembered that acceleration results from any change in speed, including changes in both its magnitude and its direction.

Tangential and normal acceleration

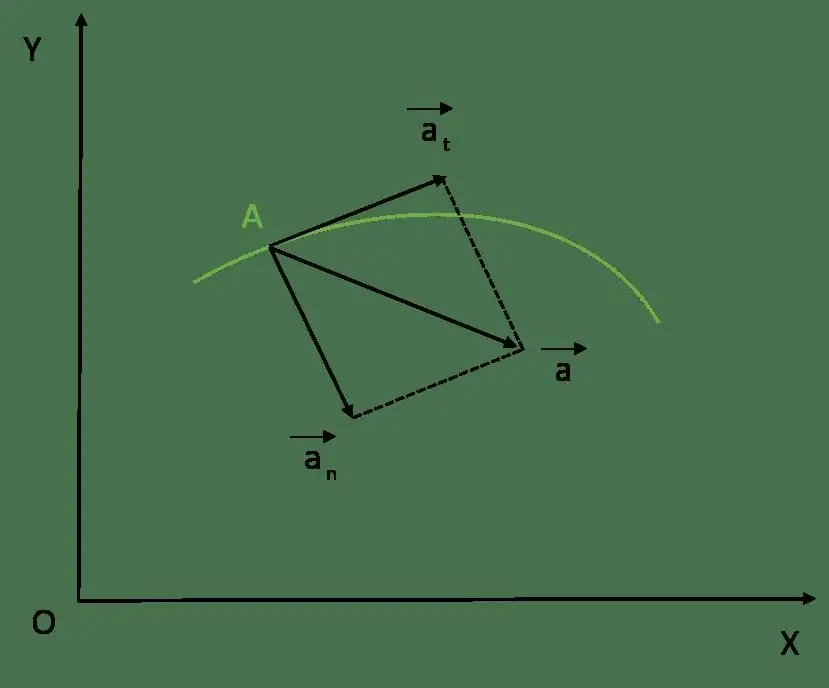
Assume that a material point moves along some curved line. It is known that at some time t its speed was equal to v¯. Since the speed is a vector tangent to the trajectory, it can be represented as follows:

v¯=v × u_t¯

Here v is the length of the vector v¯ and u_t¯ is the unit velocity vector.

To calculate the total acceleration vector at time t, you need to find the time derivative of the speed. We have:

a¯=dv¯ / dt=d (v × u_t¯) / dt

Since the modulus of speed and the unit vector change over time, then, using the rule for finding the derivative of the product of functions, we get:

a¯=dv / dt ×u_t¯ + d (u_t¯) / dt × v

The first term in the formula is called the tangential or tangential acceleration component, the second term is the normal acceleration.

Tangential acceleration

Let's write down the formula for calculating the tangential acceleration again:

a_t¯=dv / dt × u_t¯

This equality means that the tangential (tangential) acceleration is directed in the same way as the velocity vector at any point of the trajectory. It numerically determines the change in the speed modulus. For example, in the case of rectilinear motion, the total acceleration consists of only a tangential component. The normal acceleration for this type of movement is zero.

The reason for the appearance of the quantity a_t¯ is the effect of an external force on a moving body.

In the case of rotation with constant angular acceleration α, the tangential acceleration component can be calculated using the following formula:

a_t=α × r

Here r is the radius of rotation of the considered material point, for which the value a_t.

is calculated

Normal or centripetal acceleration

Now let's write the second component of the total acceleration again:

a_c¯=d (u_t¯) / dt × v

From geometrical considerations, it can be shown that the time derivative of the unit tangent to the trajectory vector is equal to the ratio of the velocity modulus v to the radius r inpoint in time t. Then the expression above will be written like this:

a_c=v² / r

This formula for normal acceleration shows that, unlike the tangential component, it does not depend on the change in speed, but is determined by the square of the modulus of the speed itself. Also, a_c increases with decreasing radius of rotation at a constant v.

Normal acceleration is called centripetal because it is directed from the center of mass of a rotating body to the axis of rotation.

The cause of this acceleration is the central component of the force acting on the body. For example, in the case of the rotation of the planets around our Sun, the centripetal force is gravitational attraction.

Normal acceleration of a body only changes the direction of the speed. It cannot change its module. This fact is its important difference from the tangential component of the total acceleration.

Since centripetal acceleration always occurs when the velocity vector rotates, it also exists in the case of uniform circular rotation, in which the tangential acceleration is zero.

In practice, you can feel the effect of normal acceleration if you are in a car when it makes a long turn. In this case, passengers are pressed against the opposite direction of rotation of the car door. This phenomenon is the result of the action of two forces: centrifugal (displacement of passengers from their seats) and centripetal (pressure on passengers from the side of the car door).

Module and direction of full acceleration

So, we found out that the tangential component of the considered physical quantity is directed tangentially to the trajectory of motion. In turn, the normal component is perpendicular to the trajectory at the given point. This means that the two acceleration components are perpendicular to each other. Their vector addition gives the full acceleration vector. You can calculate its module using the following formula:

a=√(a_t² + a_c²⁾

The direction of the vector a¯ can be determined both relative to the vector a_t¯ and relative to a_c¯. To do this, use the appropriate trigonometric function. For example, the angle between full and normal acceleration is:

φ=arccos(a_c / a)

Solution of the problem of centripetal acceleration

A wheel that has a radius of 20 cm spins with an angular acceleration of 5 rad/s² for 10 seconds. It is necessary to determine the normal acceleration of points located on the periphery of the wheel after the specified time.

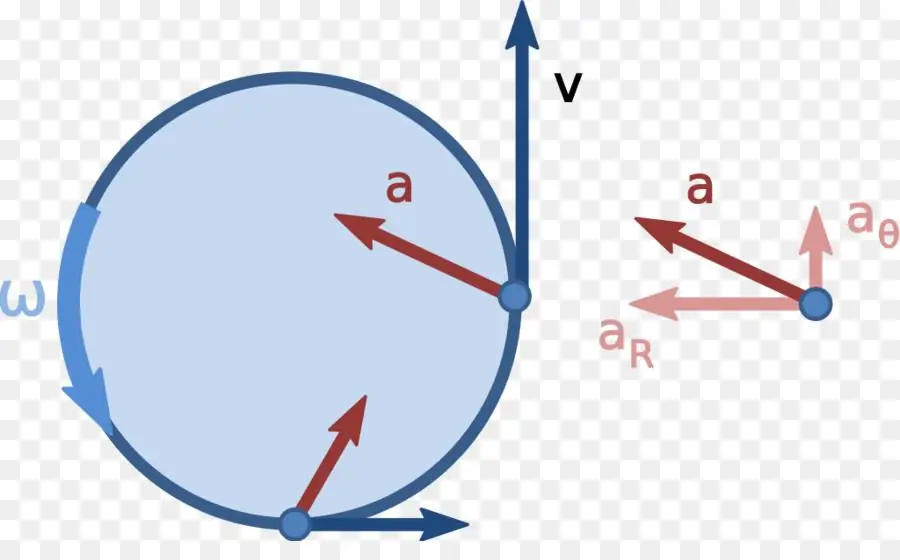
To solve the problem, we use the formula for the relationship between tangential and angular accelerations. We get:

a_t=α × r

Since the uniformly accelerated movement lasted for the time t=10 seconds, the linear speed acquired during this time was equal to:

v=a_t × t=α × r × t

We substitute the resulting formula into the corresponding expression for normal acceleration:

a_c=v² / r=α² × t ² × r

It remains to substitute the known values into this equation and write down the answer: a_c=500 m/s².