In middle school and high school students studied the topic "Fractions". However, this concept is much broader than given in the learning process. Today, the concept of a fraction occurs quite often, and not everyone can calculate any expression, for example, multiplying fractions.

What is a fraction?
It so happened historically that fractional numbers appeared because of the need to measure. As practice shows, there are often examples for determining the length of a segment, the volume of a rectangular parallelepiped, the area of a rectangle.
Initially, students are introduced to the concept of share. For example, if you divide a watermelon into 8 parts, then each will get one-eighth of a watermelon. This one part of eight is called a share.
A share equal to ½ of any value is called a half; ⅓ - third; ¼ - a quarter. Entries like 5/8, 4/5, 2/4 are called common fractions. A common fraction is divided intonumerator and denominator. Between them is a fractional line, or fractional line. A fractional bar can be drawn as either a horizontal or a slanted line. In this case, it stands for the division sign.
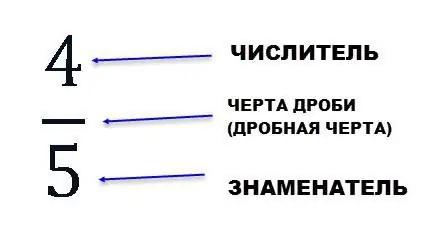
The denominator represents how many equal shares a value, an object is divided into; and the numerator is how many equal shares are taken. The numerator is written above the fractional bar, the denominator is written below it.
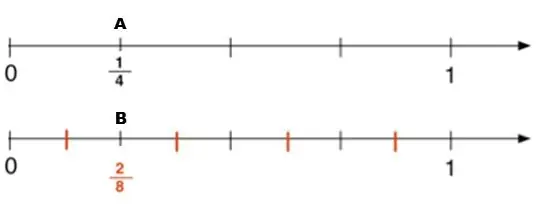
It is most convenient to show ordinary fractions on the coordinate ray. If you divide a single segment into 4 equal parts, designate each part with a Latin letter, then as a result you can get an excellent visual aid. So, point A shows a share equal to 1/4 of the entire unit segment, and point B marks 2 /8 from this segment.
Varieties of fractions
Fractions are ordinary, decimal, and also mixed numbers. In addition, fractions can be divided into proper and improper. This classification is more suitable for common fractions.
A proper fraction is a number whose numerator is less than the denominator. Accordingly, an improper fraction is a number whose numerator is greater than the denominator. The second kind is usually written as a mixed number. Such an expression consists of an integer part and a fractional part. For example, 1½. 1 - integer part, ½ - fractional. However, if you need to perform some manipulations with the expression (dividing or multiplying fractions, reducing or converting them), the mixed number is translated intoimproper fraction.
A correct fractional expression is always less than one, and an incorrect one is always greater than or equal to 1.
As for decimal fractions, this expression is understood as a record in which any number is represented, the denominator of the fractional expression of which can be expressed through one with several zeros. If the fraction is correct, then the integer part in the decimal notation will be zero.
To write a decimal, you must first write the integer part, separate it from the fractional with a comma, and then write the fractional expression. It must be remembered that after the comma the numerator must contain as many numeric characters as there are zeros in the denominator.
Example. Represent the fraction 721/1000 in decimal notation.

Algorithm for converting an improper fraction to a mixed number and vice versa
It is incorrect to write down an improper fraction in the answer of the problem, so it needs to be converted into a mixed number:
- divide the numerator by the available denominator;
- in a specific example, the incomplete quotient is an integer;
- and the remainder is the numerator of the fractional part, and the denominator remains unchanged.
Example. Convert improper fraction to mixed number: 47/5.
Decision. 47: 5. Partial quotient is 9, remainder=2. So 47/5 =92 /5.
Sometimes you need to represent a mixed number as an improper fraction. Then you need to usefollowing algorithm:
- the integer part is multiplied by the denominator of the fractional expression;
- the resulting product is added to the numerator;
- the result is written in the numerator, the denominator remains unchanged.
Example. Express a mixed number as an improper fraction: 98/10.
Decision. 9 x 10 + 8=90 + 8=98 is the numerator.
Answer: 98/10.
Multiplication of ordinary fractions
Various algebraic operations can be performed on ordinary fractions. To multiply two numbers, you need to multiply the numerator with the numerator, and the denominator with the denominator. Moreover, the multiplication of fractions with different denominators does not differ from the product of fractional numbers with the same denominators.

It happens that after finding the result, you need to reduce the fraction. It is imperative to simplify the resulting expression as much as possible. Of course, it cannot be said that an improper fraction in the answer is a mistake, but it is also difficult to call it a correct answer.
Example. Find the product of two common fractions: ½ and 20/18.
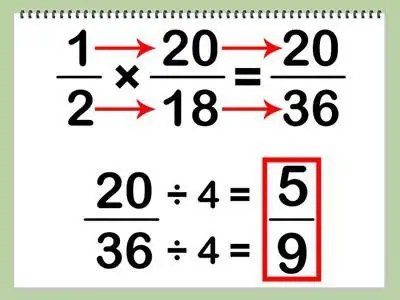
As you can see from the example, after finding the product, we get a reduced fractional notation. Both the numerator and the denominator in this case are divisible by 4, and the result is the answer 5/9.
Multiplication of decimal fractions
Artworkdecimal fractions is quite different from the product of ordinary fractions in its principle. So, multiplying fractions is as follows:
- two decimal fractions must be written under each other so that the rightmost digits are one under the other;
- you need to multiply the written numbers, despite the commas, that is, as natural numbers;
- calculate the number of digits after the comma in each of the numbers;
- in the result obtained after multiplication, you need to count as many numeric characters on the right as are contained in the sum in both factors after the decimal point, and put a separating sign;
- if there are fewer digits in the product, then you need to write as many zeros in front of them to cover this number, put a comma and assign an integer part equal to zero.

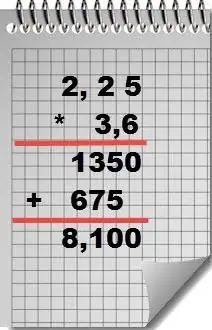
Example. Calculate the product of two decimals: 2, 25 and 3, 6.
Decision.
Multiplication of mixed fractions
To calculate the product of two mixed fractions, you need to use the rule for multiplying fractions:
- convert mixed numbers to improper fractions;
- find the product of numerators;
- find the product of the denominators;
- write down the result;
- simplify the expression as much as possible.
Example. Find the product of 4½ and 62/5.

Multiplying a number by a fraction(fractions per number)
In addition to finding the product of two fractions, mixed numbers, there are tasks where you need to multiply a natural number by a fraction.
So, to find the product of a decimal fraction and a natural number, you need:
- write the number under the fraction so that the rightmost digits are one above the other;
- find product despite comma;
- in the result, separate the integer part from the fractional part using a comma, counting to the right the number of characters that is after the decimal point in the fraction.
To multiply an ordinary fraction by a number, you should find the product of the numerator and the natural factor. If the answer is a reduced fraction, it should be converted.
Example. Compute the product of 5/8 and 12.
Decision. 5/812=(512)/8=60/8 =30/4 =15/2 =71/2.
Answer: 71/2.
As you can see from the previous example, it was necessary to reduce the resulting result and convert the incorrect fractional expression into a mixed number.
Also, the multiplication of fractions also applies to finding the product of a number in mixed form and a natural factor. To multiply these two numbers, you should multiply the integer part of the mixed factor by the number, multiply the numerator by the same value, and leave the denominator unchanged. If necessary, simplify the result as much as possible.
Example. To findthe product of 95/6 and 9.
Decision. 95/6 x 9=9 x 9 + (5 x 9)/ 6 =81 + 45/6 =81 + 73/ 6 =881/2.
Answer: 881/2.
Multiply by factors 10, 100, 1000 or 0, 1; 0.01; 0, 001
The following rule follows from the previous paragraph. To multiply a decimal fraction by 10, 100, 1000, 10000, etc., you need to move the comma to the right by as many digit characters as there are zeros in the multiplier after one.
Example 1. Find the product of 0, 065 and 1000.
Decision. 0.065 x 1000=0065=65.
Answer: 65.
Example 2. Find the product of 3, 9 and 1000.
Decision. 3.9 x 1000=3.900 x 1000=3900.
Answer: 3900.
If you need to multiply a natural number and 0, 1; 0.01; 0.001; 0, 0001, etc., you should move the comma to the left in the resulting product by as many digit characters as there are zeros before one. If necessary, a sufficient number of zeros are written before the natural number.
Example 1. Find the product of 56 and 0, 01.
Decision. 56 x 0.01=0056=0.56.
Answer: 0, 56.
Example 2. Find the product of 4 and 0, 001.
Decision. 4 x 0.001=0004=0.004.
Answer: 0, 004.
So, finding the product of various fractions should not be difficult, except perhaps the calculation of the result; in this case, you simply cannot do without a calculator.






