Reducing ordinary fractions is taught at school in mathematics lessons. If you are a student who has safely missed this topic or did not understand it, or if you are the parent of such a student, then this topic is just for you. How to reduce a fraction? Easy and simple if you follow the method below.
What is a common fraction
Recall the theory. Ordinary fractions appear as a result of dividing an object or unit of measurement into several equal parts. Let's take pie as an example. If you cut it into ten parts and give these ten parts to ten guests, then in an ordinary fraction it will look like 1/10 (one tenth). But on the letter, this will be reflected in a two-story entry, in which a number above the dash indicates how many parts were taken, and below the dash is their total number.
For example, the fraction 2/5 means that a person took only two out of five parts of something.
Let's move on to the main question: how to reduce a fraction?
What does it mean
Reducing a fraction means dividing the numerator (the number above the line) and the denominator (the number below the line) by the samethe same number (it must be greater than one). Moreover, it is necessary to divide until the numerator and denominator have a total number by which they could be divided.
Reduced fractions are fractions that cannot be further reduced. They are not considered reduced if the numerator and denominator still have a common number by which to divide each of them.
Abbreviation
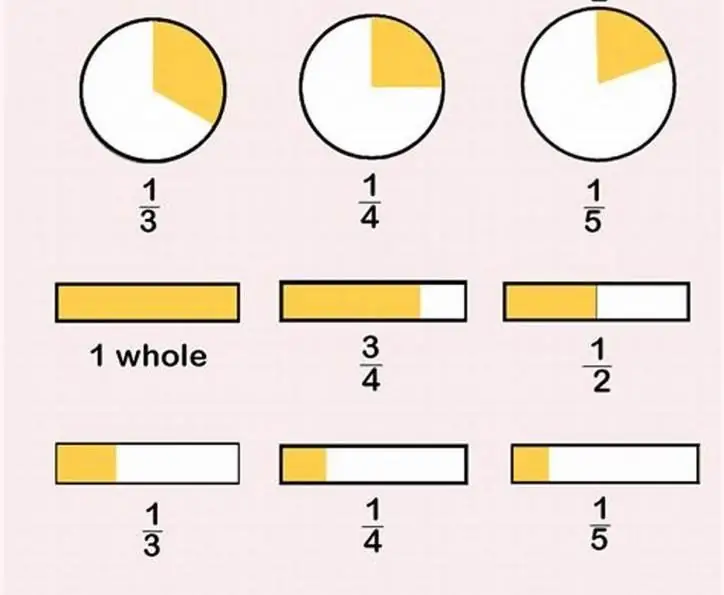
That's sorted out, let's move on to the next question. Let's look at examples of how to reduce a fraction.
Take the fraction 5/25. By what number do we divide? For five. Let's reduce the numerator and denominator by it. The result is the number 1/5. Can you cut further? No.
Or fraction 60/120. By what number can they be divided? For thirty. We reduce and get the number 2/4. Can you cut further? Yes, you can cut two more. Get 1/2.
How to reduce the fraction "to the winning number", that is, not to divide it several times? Just try to find the largest number that divides the numerator and denominator. When we analyzed the second example, the fraction 60/120, it could be divided by sixty and immediately get 1/2.
If the largest number is not immediately found, then first try to divide the fraction by any number that came to your mind, and try to work with the new fraction again. The main thing is to correctly and completely reduce the fraction. It doesn't matter how many steps you took to get there, but if you value your time, try to complete everything in one step.






