Plane equations. Angle between two planes

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

A plane, along with a point and a straight line, is a basic geometric element. With its use, many figures in spatial geometry are built. In this article, we will consider in more detail the question of how to find an angle between two planes.

Concept

Before talking about the angle between two planes, you should understand well what element in geometry we are talking about. Let's understand the terminology. A plane is an endless collection of points in space, connecting which we get vectors. The latter will be perpendicular to some one vector. It is commonly called the normal to the plane.

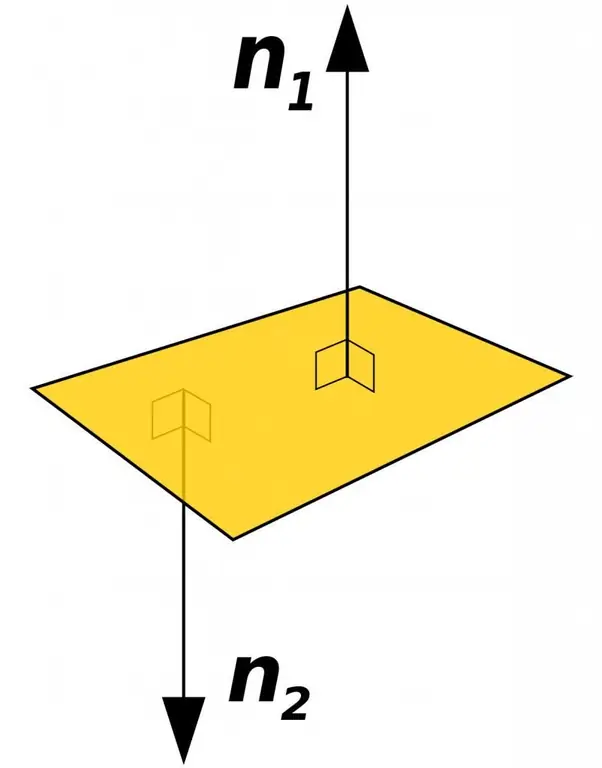
The figure above shows a plane and two normal vectors to it. It can be seen that both vectors lie on the same straight line. The angle between them is 180o.

Equations

The angle between two planes can be determined if the mathematical equation of the considered geometric element is known. There are several types of such equations,whose names are listed below:

• general type;
• vector;
• in segments.

These three types are the most convenient for solving various kinds of problems, so they are most often used.

A general type equation looks like this:

Ax + By + Cz + D=0.

Here x, y, z are the coordinates of an arbitrary point belonging to the given plane. Parameters A, B, C and D are numbers. The convenience of this notation lies in the fact that the numbers A, B, C are the coordinates of a vector normal to the plane.

The vector form of the plane can be represented as follows:

x, y, z)=(x₀, y₀, z₀) + α(a₁, b₁, c₁) + β(a ₂, b₂, c_2).

Here (a₂, b₂, c₂) and (a ₁, b₁, c₁) - parameters of two coordinate vectors that belong to the considered plane. The point (x₀, y₀, z_{0) also lies in this plane. Parameters α and β can take independent and arbitrary values.}

Finally, the equation of the plane in segments is represented in the following mathematical form:

x/p + y/q + z/l=1.

Here p, q, l are specific numbers (including negative ones). This kind of equation is useful when it is necessary to depict a plane in a rectangular coordinate system, since the numbers p, q, l show the points of intersection with the x, y and z axesplane.

Note that each type of equation can be converted to any other using simple mathematical operations.

Formula for the angle between two planes

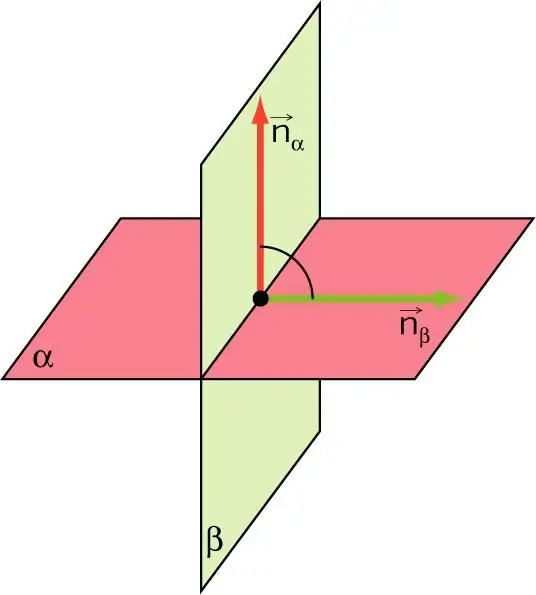
Now consider the following nuance. In three-dimensional space, two planes can be located in only two ways. Either intersect or be parallel. Between two planes, the angle is what is located between their guide vectors (normal). Intersecting, 2 vectors form 2 angles (acute and obtuse in the general case). The angle between the planes is considered to be acute. Consider the equation.

The formula for the angle between two planes is:

θ=arccos(|(n₁¯n₂¯)|/(|n₁ ¯||n_2¯|)).

It is easy to guess that this expression is a direct consequence of the scalar product of the normal vectors n₁¯ and n₂¯ for the considered planes. The modulus of the dot product in the numerator indicates that the angle θ will only take values from 0^o to 90^{o. The product of the modules of normal vectors in the denominator means the product of their lengths.}

Note, if (n₁¯n_{2¯)=0, then the planes intersect at a right angle.}

Example problem

Having figured out what is called the angle between two planes, we will solve the following problem. As an example. So, it is necessary to calculate the angle between such planes:

2x - 3y + 4=0;

(x, y, z)=(2, 0, -1) + α(1, 1, -1) + β(0, 2, 3).

To solve the problem, you need to know the direction vectors of the planes. For the first plane, the normal vector is: n₁¯=(2, -3, 0). To find the second plane normal vector, one should multiply the vectors after the parameters α and β. The result is a vector: n_{2¯=(5, -3, 2).}

To determine the angle θ, we use the formula from the previous paragraph. We get:

θ=arccos (|((2, -3, 0)(5, -3, 2))|/(|(2, -3, 0)||(5, -3, 2)|))=

=arccos (19/√(1338))=0.5455 rad.

The calculated angle in radians corresponds to 31.26^o. Thus, the planes from the condition of the problem intersect at an angle of 31, 26^o.