Trapezoid is a geometric figure with four corners. When constructing a trapezoid, it is important to consider that two opposite sides are parallel, while the other two, on the contrary, are not parallel to each other. This word came into modern times from Ancient Greece and sounded like "trapezion", which meant "table", "dining table".
This article talks about the properties of a trapezoid circumscribed about a circle. We will also consider the types and elements of this figure.
Elements, types and signs of a geometric figure trapezoid
Parallel sides in this figure are called bases, and those that are not parallel are called sides. Provided that the sides are the same length, the trapezoid is considered isosceles. A trapezoid, the sides of which lie perpendicular to the base at an angle of 90 °, is called a rectangular one.
This seemingly uncomplicated figure has a considerable number of properties inherent in it, emphasizing its features:
- If you draw the middle line along the sides, it will be parallel to the bases. This segment will be equal to 1/2 of the base difference.
- When constructing a bisector from any angle of a trapezoid, an equilateral triangle is formed.
- From the properties of a trapezoid circumscribed about a circle, it is known that the sum of the parallel sides must be equal to the sum of the bases.
- When constructing diagonal segments, where one of the sides is the base of a trapezoid, the resulting triangles will be similar.
- When constructing diagonal segments, where one of the sides is lateral, the resulting triangles will have the same area.
- If you continue the side lines and build a segment from the center of the base, then the formed angle will be equal to 90°. The segment connecting the bases will be equal to 1/2 of their difference.
Properties of a trapezoid circumscribed about a circle
It is possible to enclose a circle into a trapezoid only under one condition. This condition is that the sum of the sides must be equal to the sum of the bases. For example, when constructing a trapezoid AFDM, AF + DM=FD + AM is applicable. Only in this case, you can make a circle into a trapezoid.
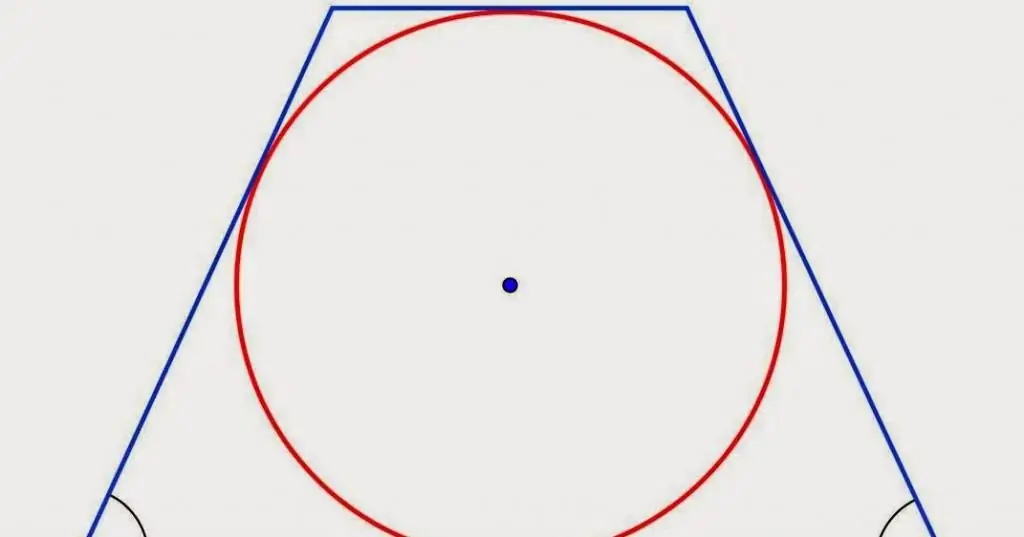
So, more about the properties of a trapezoid circumscribed about a circle:
- If a circle is enclosed in a trapezoid, then in order to find the length of its line that intersects the figure in half, you need to find 1/2 of the sum of the lengths of the sides.
- When constructing a trapezoid circumscribed about a circle, the formed hypotenuseis identical to the radius of the circle, and the height of the trapezoid is also the diameter of the circle.
- Another property of an isosceles trapezoid circumscribed about a circle is that its lateral side is immediately visible from the center of the circle at an angle of 90°.
A little more about the properties of a trapezoid enclosed in a circle
Only an isosceles trapezoid can be inscribed in a circle. This means that it is necessary to meet the conditions under which the constructed AFDM trapezoid will meet the following requirements: AF + DM=FD + MA.
Ptolemy's theorem states that in a trapezoid enclosed in a circle, the product of the diagonals is identical and equal to the sum of the multiplied opposite sides. This means that when constructing a circle circumscribing a trapezoid AFDM, the following applies: AD × FM=AF × DM + FD × AM.
It's quite common in school exams to solve problems with a trapezoid. A large number of theorems must be memorized, but if you don’t succeed in learning right away, it doesn’t matter. It is best to periodically resort to a hint in textbooks so that this knowledge by itself, without much difficulty, fits into your head.






