Even in ancient Egypt, science appeared, with the help of which it was possible to measure volumes, areas and other quantities. The impetus for this was the construction of the pyramids. It involved a significant number of complex calculations. And besides construction, it was important to properly measure the land. Hence the science of "geometry" appeared from the Greek words "geos" - earth and "metrio" - I measure.
The study of geometric forms was facilitated by the observation of astronomical phenomena. And already in the 17th century BC. e. the initial methods for calculating the area of a circle, the volume of a ball were found, and the most important discovery was the Pythagorean theorem.
The statement of the theorem about a circle inscribed in a triangle is as follows:
Only one circle can be inscribed in a triangle.
With this arrangement, the circle is inscribed, and the triangle is circumscribed near the circle.
The statement of the theorem about the center of a circle inscribed in a triangle is as follows:
Central point of a circle inscribed intriangle, there is a point of intersection of the bisectors of this triangle.
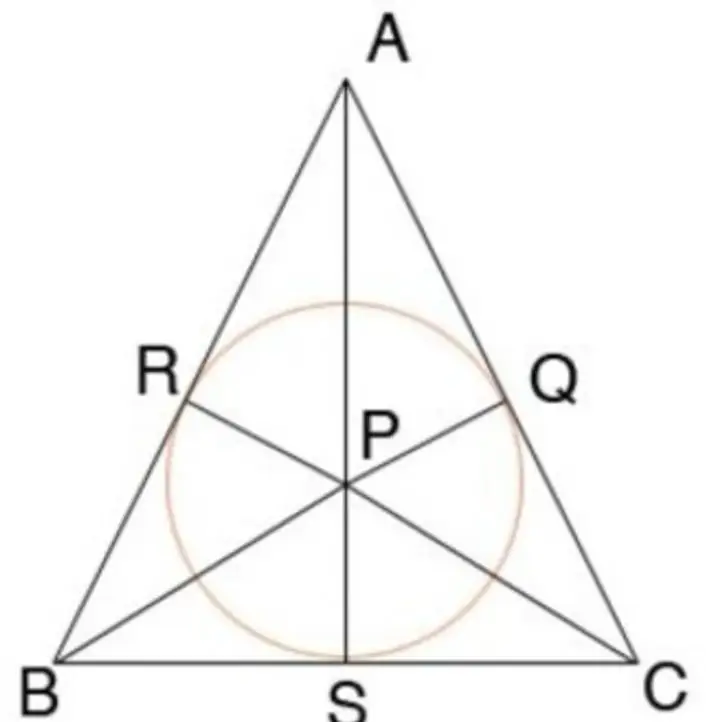
Circle inscribed in an isosceles triangle
A circle is considered inscribed in a triangle if it touches all its sides with at least one point.
The photo below shows a circle inside an isosceles triangle. The condition of the theorem about a circle inscribed in a triangle is met - it touches all sides of the triangle AB, BC, and CA at points R, S, Q, respectively.
One of the properties of an isosceles triangle is that the inscribed circle bisects the base by the point of contact (BS=SC), and the radius of the inscribed circle is one third of the height of this triangle (SP=AS/3).
Properties of the triangle incircle theorem:
- Segments coming from one vertex of the triangle to the points of contact with the circle are equal. In the picture AR=AQ, BR=BS, CS=CQ.
- The radius of a circle (inscribed) is the area divided by the half-perimeter of the triangle. As an example, you need to draw an isosceles triangle with the same letter designations as in the picture, of the following dimensions: base BC \u003d 3 cm, height AS \u003d 2 cm, sides AB \u003d BC, respectively, are obtained by 2.5 cm each. We draw a bisector from each corner and denote the place of their intersection as P. We inscribe a circle with radius PS, the length of which must be found. You can find out the area of a triangle by multiplying 1/2 of the base by the height: S=1/2DCAS=1/232=3 cm2. Semiperimetertriangle is equal to 1/2 of the sum of all sides: P \u003d (AB + BC + SA) / 2 \u003d (2.5 + 3 + 2.5) / 2 \u003d 4 cm; PS=S/P=3/4=0.75 cm2, which is completely true when measured with a ruler. Accordingly, the property of the theorem about a circle inscribed in a triangle is true.
Circle inscribed in a right triangle
For a triangle with a right angle, the properties of the triangle inscribed circle theorem apply. And, in addition, the ability to solve problems with the postulates of the Pythagorean theorem is added.
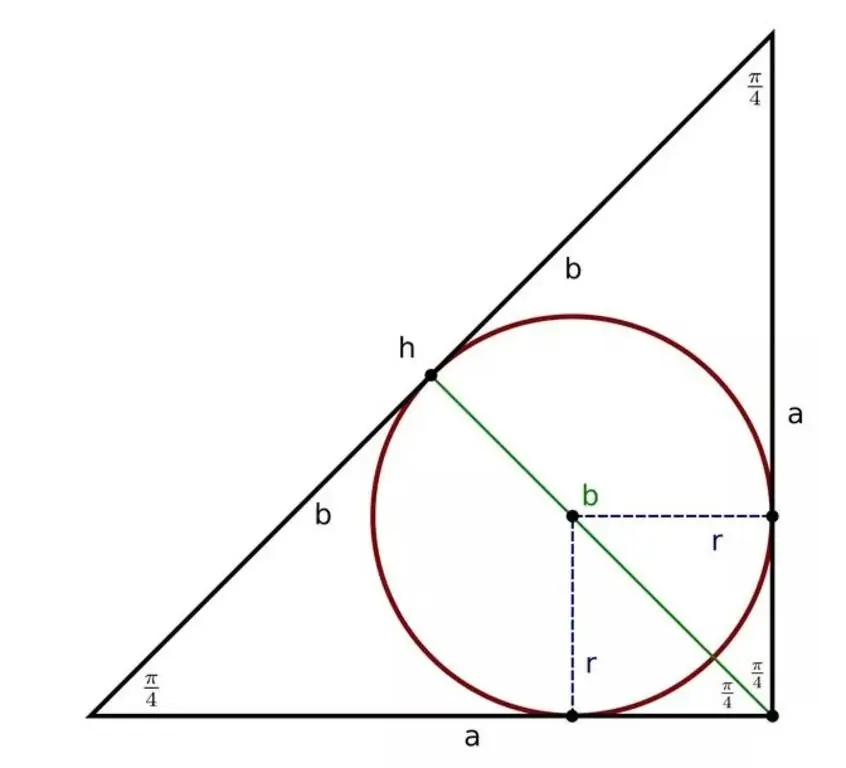
The radius of the inscribed circle in a right triangle can be determined as follows: add the lengths of the legs, subtract the value of the hypotenuse and divide the resulting value by 2.
There is a good formula that will help you calculate the area of a triangle - multiply the perimeter by the radius of the circle inscribed in this triangle.
Formulation of the incircle theorem
Theorems about inscribed and circumscribed figures are important in planimetry. One of them sounds like this:
The center of a circle inscribed in a triangle is the intersection point of the bisectors drawn from its corners.
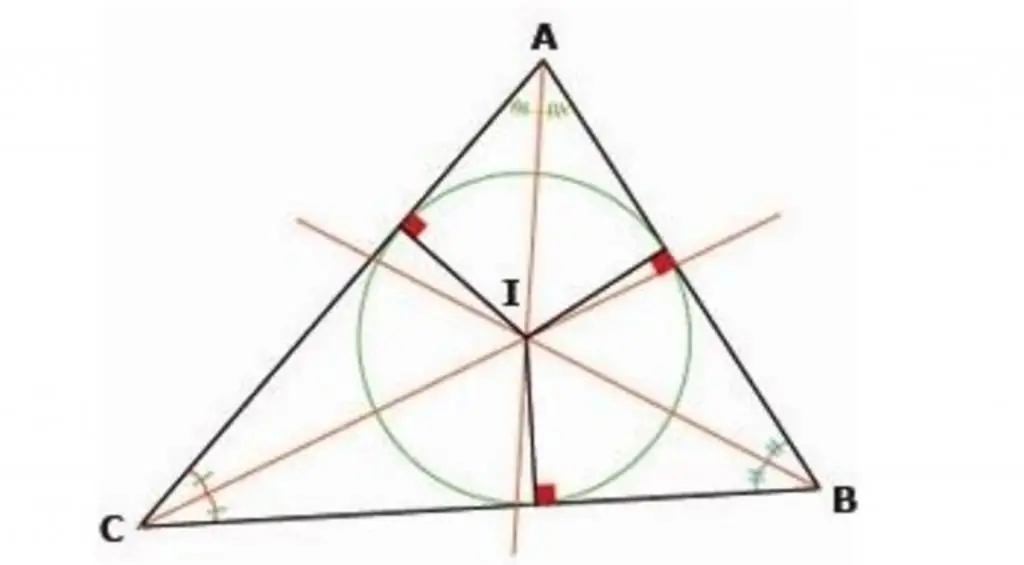
The figure below shows the proof of this theorem. The equality of angles is shown, and, accordingly, the equality of adjacent triangles.
Theorem about the center of a circle inscribed in a triangle
The radii of a circle inscribed in a triangle,drawn to the points of contact are perpendicular to the sides of the triangle.
The task "formulate the theorem about a circle inscribed in a triangle" should not be taken by surprise, because this is one of the fundamental and simplest knowledge in geometry, which must be fully mastered to solve many practical problems in real life.






