Every student knows that when there is contact between two solid surfaces, the so-called friction force arises. Let's consider in this article what it is, focusing on the point of application of the friction force.
What kinds of friction force are there?
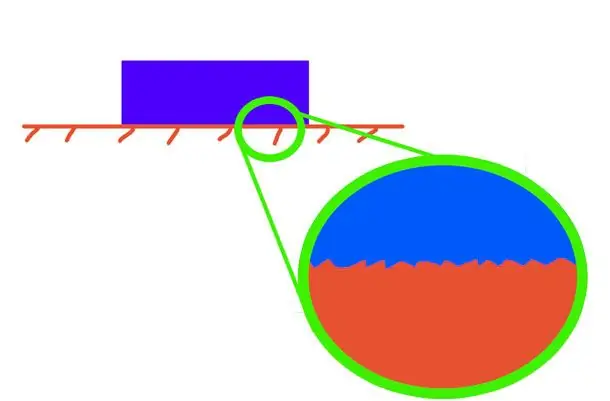
Before considering the point of application of the friction force, it is necessary to briefly recall what types of friction exist in nature and technology.
Let's start to consider static friction. This type characterizes the state of a solid body at rest on some surface. The friction of rest prevents any displacement of the body from its state of rest. For example, due to the action of this very force, it is difficult for us to move a cabinet standing on the floor.
Sliding friction is another kind of friction. It manifests itself in the case of contact between two surfaces sliding on each other. Sliding friction impedes movement (the direction of the friction force is opposite to the velocity of the body). A striking example of its action is a skier or skater sliding on ice on snow.
Finally, the third type of friction is rolling. It always exists when one body rolls on the surface of another. For example, the rolling of a wheel or bearings are prime examples where rolling friction is important.
The first two of the described types arise due to roughness on rubbing surfaces. The third type arises due to the deformation hysteresis of the rolling body.
Points of application of sliding and rest friction forces
It was said above that the static friction prevents the external acting force, which tends to move the object along the contact surface. This means that the direction of the friction force is opposite to the direction of the external force parallel to the surface. The point of application of the considered friction force is in the area of contact between two surfaces.
It is important to understand that the static friction force is not a constant value. It has a maximum value, which is calculated using the following formula:
Ft=µtN.
However, this maximum value appears only when the body starts its movement. In any other case, the static friction force is exactly equal in absolute value to the parallel surface of the external force.
As for the point of application of the force of sliding friction, it does not differ from that for static friction. Speaking about the difference between static and sliding friction, the absolute significance of these forces should be noted. Thus, the force of sliding friction for a given pair of materials is a constant value. In addition, it is always less than the maximum force of static friction.
As you can see, the point of application of friction forces does not coincide with the center of gravity of the body. This means that the forces under consideration create a moment tending to overturn the sliding body forward. The latter can be observed when the cyclist brakes hard with the front wheel.

Rolling friction and its application point
Since the physical cause of the rolling friction is different from that for the types of friction discussed above, the point of application of the rolling friction force has a slightly different character.
Assume that the wheel of the car is on the pavement. It is obvious that this wheel is deformed. The area of its contact with asph alt is equal to 2dl, where l is the width of the wheel, 2d is the length of the lateral contact of the wheel and asph alt. The force of rolling friction, in its physical essence, manifests itself in the form of a reaction moment of the support directed against the rotation of the wheel. This moment is calculated as follows:
M=Nd
If we divide it and multiply it by the radius of the wheel R, then we get:
M=Nd/RR=FtR where Ft=Nd/R
Thus, the rolling friction force Ft is actually the reaction of the support, creating a moment of force that tends to slow down the rotation of the wheel.
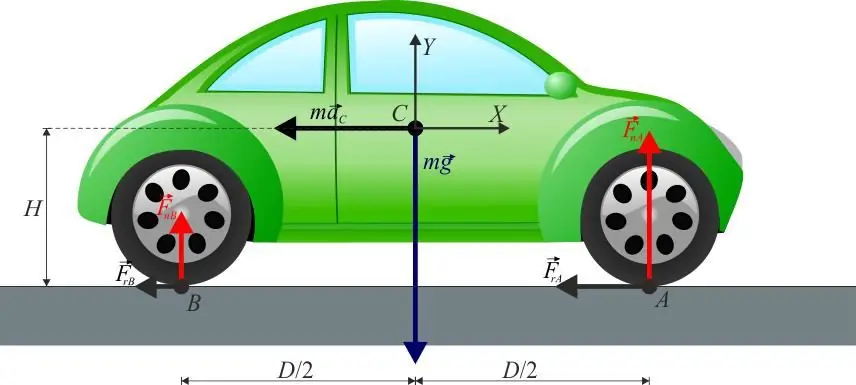
The point of application of this force is directed vertically upward relative to the surface of the plane and is shifted to the right from the center of mass by d (assuming that the wheel moves from left to right).
Example of problem solving
Actionfriction force of any kind tends to slow down the mechanical movement of bodies, while converting their kinetic energy into heat. Let's solve the following problem:
bar slides on an inclined surface. It is necessary to calculate the acceleration of its movement if it is known that the coefficient for sliding is 0.35, and the angle of inclination of the surface is 35o.
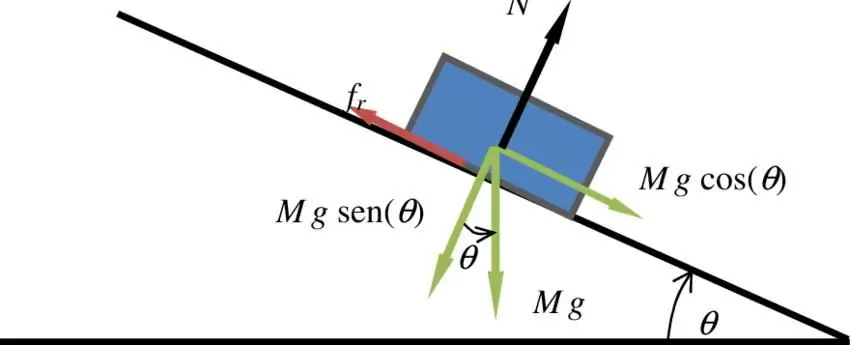
Let's consider what forces act on the bar. First, the gravity component is directed downward along the sliding surface. It is equal to:
F=mgsin(α)
Secondly, a constant friction force acts upward along the plane, which is directed against the acceleration vector of the body. It can be determined by the formula:
Ft=µtN=µtmgcos (α)
Then Newton's law for a bar moving with acceleration a will take the form:
ma=mgsin(α) - µtmgcos(α)=>
a=gsin(α) - µtgcos(α)
Substituting the data into equality, we get that a=2.81 m/s2. Note that the found acceleration does not depend on the mass of the bar.






