Rolling friction force: description, formula

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

Friction is a physical phenomenon that a person struggles with in order to reduce it in any rotating and sliding parts of mechanisms, without which, however, the movement of any of these mechanisms is impossible. In this article, we will consider, from the point of view of physics, what is the force of rolling friction.

What types of friction forces exist in nature?

First of all, consider what place rolling friction takes among other friction forces. These forces arise as a result of the contact of two different bodies. It can be solid, liquid or gaseous bodies. For example, the flight of an aircraft in the troposphere is accompanied by the presence of friction between its body and air molecules.

Considering exclusively solid bodies, we single out the friction forces of rest, sliding and rolling. Each of us noticed: in order to budge a box on the floor, it is necessary to apply some force along the floor surface. The value of the force that will bring the boxes out of rest will be equal in absolute value to the rest friction force. The latter acts between the bottom of the box and the floor surface.

Howonce the box has begun its movement, a constant force must be applied to keep this movement uniform. This fact is connected with the fact that between the contact of the floor and the box, the sliding friction force acts on the latter. As a rule, it is several tens of percent less than the static friction.

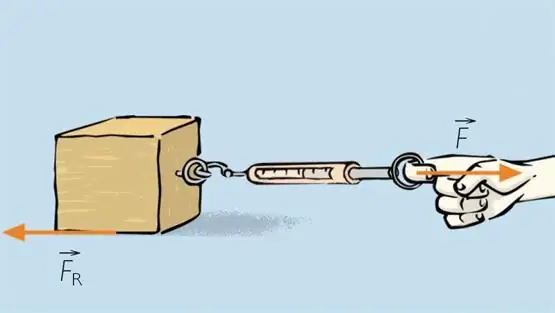
If you put round cylinders of hard material under the box, it will become much easier to move it. The rolling friction force will act on the cylinders rotating in the process of movement under the box. It is usually much smaller than the previous two forces. That is why the invention of the wheel by mankind was a huge leap towards progress, because people were able to move much larger loads with little applied force.

Physical nature of rolling friction

Why does rolling friction occur? This question is not easy. To answer it, one should consider in detail what happens to the wheel and the surface during the rolling process. First of all, they are not perfectly smooth - neither the surface of the wheel, nor the surface on which it rolls. However, this is not the main cause of friction. The main reason is the deformation of one or both bodies.

Any bodies, no matter what solid material they are made of, are deformed. The greater the weight of the body, the greater the pressure it exerts on the surface, which means that it deforms itself at the point of contact and deforms the surface. This deformation in some cases is so small that it does not exceed the elastic limit.

Bduring the rolling of the wheel, the deformed areas after the termination of contact with the surface restore their original shape. Nevertheless, these deformations are cyclically repeated with a new revolution of the wheel. Any cyclic deformation, even if it lies in the elastic limit, is accompanied by hysteresis. In other words, at the microscopic level, the shape of the body before and after deformation is different. The hysteresis of deformation cycles during the rolling of the wheel leads to the "dispersion" of energy, which manifests itself in practice in the form of the appearance of a rolling friction force.

Perfect Body Rolling

Under the ideal body in this case we mean that it is non-deformable. In the case of an ideal wheel, its contact area with the surface is zero (it touches the surface along the line).

Let's characterize the forces that act on a non-deformable wheel. Firstly, these are two vertical forces: body weight P and support reaction force N. Both forces pass through the center of mass (wheel axis), therefore, they do not take part in the creation of torque. For them, you can write:

P=N

Secondly, these are two horizontal forces: an external force F that pushes the wheel forward (it passes through the center of mass), and a rolling friction force f_r. The latter creates a torque M. For them, you can write the following equalities:

M=f_rr;

F=f_r

Here r is the radius of the wheel. These equalities contain a very important conclusion. If the friction force f_r is infinitely small, then itwill still create a torque that will cause the wheel to move. Since the external force F is equal to f_r, then any infinitely small value of F will cause the wheel to roll. This means that if the rolling body is ideal and does not experience deformation during movement, then there is no need to talk about any rolling friction force.

All existing bodies are real, that is, they experience deformation.

Real body rolling

Now consider the situation described above only for the case of real (deformable) bodies. The area of contact between the wheel and the surface will no longer be zero, it will have some finite value.

Let's analyze the forces. Let's start with the action of vertical forces, that is, the weight and reaction of the support. They are still equal to each other, that is:

N=P

However, the force N now acts vertically upwards not through the wheel axle, but is slightly shifted from it by a distance d. If we represent the area of contact of the wheel with the surface as the area of a rectangle, then the length of this rectangle will be the thickness of the wheel, and the width will be equal to 2d.

Now let's move on to the consideration of horizontal forces. The external force F still does not create a torque and is equal to the friction force f_r in absolute value, that is:

F=f_r.

The moment of forces leading to rotation will create friction f_rand the reaction of the support N. Moreover, these moments will be directed in different directions. The corresponding expression istype:

M=Nd - f_rr

In the case of uniform motion, the moment M will be equal to zero, so we get:

Nd - f_rr=0=>

f_r=d/rN

The last equality, taking into account the formulas written above, can be rewritten as follows:

F=d/rP

In fact, we got the main formula for understanding the rolling friction force. Further in the article we will analyze it.

Rolling resistance coefficient

This coefficient has already been introduced above. A geometric explanation was also given. We are talking about the value of d. Obviously, the larger this value, the greater the moment creates the reaction force of the support, which prevents the movement of the wheel.

The rolling resistance coefficient d, in contrast to the coefficients of static and sliding friction, is a dimensional value. It is measured in units of length. In tables, it is usually given in millimeters. For example, for train wheels rolling on steel rails, d=0.5 mm. The value of d depends on the hardness of the two materials, the load on the wheel, the temperature and some other factors.

Rolling friction coefficient

Don't confuse it with the previous coefficient d. The rolling friction coefficient is denoted by the symbol C_r and is calculated using the following formula:

C_r=d/r

This equality means that C_r is dimensionless. It is she who is given in a number of tables containing information on the considered type of friction. This coefficient is convenient to use for practical calculations,because it does not involve knowing the radius of the wheel.

The value of C_r in most cases is less than the coefficients of friction and rest. For example, for car tires moving on asph alt, the value of C_r is within a few hundredths (0.01 - 0.06). However, it increases significantly when running flat tires on grass and sand (≈0.4).

Analysis of the resulting formula for the force fr

Let's write again the above formula for the rolling friction force:

F=d/rP=f_r

From equality it follows that the larger the diameter of the wheel, the less force F should be applied in order for it to start moving. Now we write this equality through the coefficient C_r, we have:

f_r=C_rP

As you can see, the force of friction is directly proportional to the weight of the body. In addition, with a significant increase in the weight P, the coefficient C_r itself changes (it increases due to the increase in d). In most practical cases, C_r lies within a few hundredths. In turn, the value of the coefficient of sliding friction lies within a few tenths. Since the formulas for rolling and sliding friction forces are the same, rolling turns out to be beneficial from an energy point of view (the force f_r is an order of magnitude less than the sliding force in most practical situations).

Rolling condition

Many of us have experienced the problem of car wheels slipping when driving on ice or mud. Why is thishappening? The key to answering this question lies in the ratio of the absolute values of the rolling and rest friction forces. Let's write out the rolling formula again:

F ≧ C_rP

When the force F is greater than or equal to the rolling friction, then the wheel will start to roll. However, if this force exceeds the value of static friction earlier, then the wheel will slip earlier than its rolling.

Thus, the slip effect is determined by the ratio of the coefficients of static friction and rolling friction.

Ways to counteract car wheel slip

The rolling friction of a car wheel on a slippery surface (for example, on ice) is characterized by the coefficient C_r=0.01-0.06. However, values of the same order are typical for the coefficient static friction.

To avoid the risk of wheel slippage, special "winter" tires are used, into which metal spikes are screwed. The latter, crashing into the ice surface, increase the coefficient of static friction.