In a special section of physics - dynamics, when they study the movement of bodies, they consider the forces acting on the moving system. The latter can perform both positive and negative work. Consider in this article what the work of the friction force is and how it is calculated.
The concept of work in physics
In physics, the concept of "work" is different from the ordinary idea of this word. Work is understood as a physical quantity, which is equal to the scalar product of the force vector and the displacement vector of the body. Assume that there is some object on which the force F¯ acts. Since no other forces act on it, its displacement vector l¯ will coincide in direction with the vector F¯. The scalar product of these vectors in this case will correspond to the product of their modules, that is:
A=(F¯l¯)=Fl.
The value A is the work done by the force F¯ to move the object a distance l. Taking into account the dimensions of the values F and l, we find that the work is measured in newtons per meter (Nm) in the SI system. However, the unitNm has its own name - it is a joule. This means that the concept of work is the same as the concept of energy. In other words, if a force of 1 newton moves a body 1 meter, then the corresponding energy costs are 1 joule.
What is the force of friction?
Studying the question of the work of the friction force is possible if you know what kind of force we are talking about. Friction in physics is a process that prevents any movement of one body on the surface of another when these surfaces are brought into contact.
If we consider only solid bodies, then there are three types of friction for them:
- rest;
- slip;
- rolling.
These forces act between contacting surfaces and are always directed against the movement of bodies.
Resting friction prevents the movement itself, sliding friction manifests itself in the process of movement, when the surfaces of bodies slide over each other, and rolling friction exists between the body that rolls on the surface and the surface itself.
An example of the action of static friction is a car that is on the handbrake on a hillside. Sliding friction manifests itself when a skier moves on snow or a skater moves on ice. Finally, rolling friction acts while the car's wheel is moving along the road.
Forces for all three types of friction are calculated using the following formula:
Ft=µtN.
Here N is the support reaction force, µt is the friction coefficient. Force Nshows the magnitude of the impact of the support on the body perpendicular to the plane of the surface. As for the parameter µt, it is measured experimentally for each pair of rubbing materials, for example, wood-wood, steel-snow, and so on. The measured results are collected in special tables.
For each friction force, the coefficient µt has its own value for the selected pair of materials. Thus, the coefficient of static friction is greater than that for sliding friction by several tens of percent. In turn, the rolling coefficient is 1-2 orders of magnitude less than that for sliding.
Work of friction forces
Now, having become acquainted with the concepts of work and with the types of friction, you can go directly to the topic of the article. Let's consider in order all types of friction forces and figure out what work they do.
Let's start with static friction. This type manifests itself when the body is not moving. Since there is no movement, its displacement vector l¯ is equal to zero. The latter means that the work of the static friction force is also equal to zero.
Sliding friction, by definition, acts only when the body is moving in space. Since the force of this type of friction is always directed against the movement of the body, it means that it does negative work. The value of A can be calculated using the formula:
A=-Ftl=-µtNl.
The work of the sliding friction force is aimed at slowing down the movement of the body. As a result of this work, the mechanical energy of the body is converted into heat.

Rolling friction, like sliding, also involves body movement. The rolling friction force does negative work, slowing down the initial rotation of the body. Since we are talking about the rotation of the body, it is convenient to calculate the value of the work of this force through the work of its momentum. The corresponding formula is written as:
A=-Mθ where M=FtR.
Here θ is the angle of rotation of the body as a result of rotation, R is the distance from the surface to the axis of rotation (wheel radius).
Problem with sliding friction force
It is known that a wooden block is on the edge of an inclined wooden plane. The plane is inclined to the horizon at an angle of 40o. Knowing that the coefficient of sliding friction is 0.4, the length of the plane is 1 meter, and the mass of the bar corresponds to 0.5 kg, it is necessary to find the work of sliding friction.
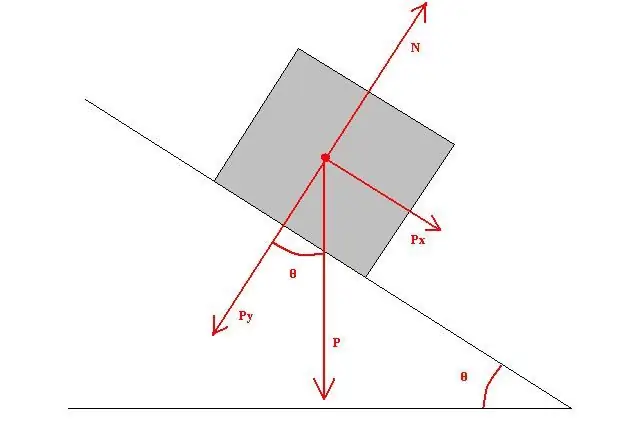
Calculate the force of sliding friction. It is equal to:
Ft=mgcos(α)µt=0.59.81cos(40 o)0, 4=1.5 N.
Then the corresponding work A will be:
A=-Ftl=-1.51=-1.5 J.
Rolling friction problem
It is known that the wheel rolled along the road for some distance and stopped. The diameter of the wheel is 45 cm. The number of revolutions of the wheel before stopping is 100. Taking into account the rolling coefficient equal to 0.03, it is necessary to find what the work of the rolling friction force is equal to. The mass of the wheel is 5 kg.

First, let's calculate the rolling friction moment:
M=FtR=µtmgD/2=0.0359, 810, 45/2=0, 331 Nm.
If the number of revolutions made by the wheel is multiplied by 2pi radians, then we get the angle of rotation of the wheel θ. Then the formula for work is:
A=-Mθ=-M2pin.
Where n is the number of revolutions. Substituting the moment M and the number n from the condition, we obtain the required work: A=- 207.87 J.






