An important concept in mathematics is a function. With its help, you can visualize many processes occurring in nature, reflect the relationship between certain quantities using formulas, tables and images on a graph. An example is the dependence of the pressure of a liquid layer on a body on the depth of immersion, acceleration - on the action of a certain force on an object, temperature increase - on the transmitted energy, and many other processes. The study of a function involves the construction of a graph, the clarification of its properties, the scope and values, intervals of increase and decrease. An important point in this process is finding the extremum points. About how to do it right, and the conversation will go on.

About the concept itself on a specific example
In medicine, plotting a function graph can tell about the progress of a disease in a patient's body, visually reflecting his condition. Let's assume that the time in days is plotted along the OX axis, and the temperature of the human body is plotted along the OY axis. The figure clearly shows how this indicator rises sharply, andthen it falls. It is also easy to notice singular points that reflect the moments when the function, having previously increased, begins to decrease, and vice versa. These are extremum points, that is, critical values (maximum and minimum) in this case of the patient's temperature, after which changes in his condition occur.
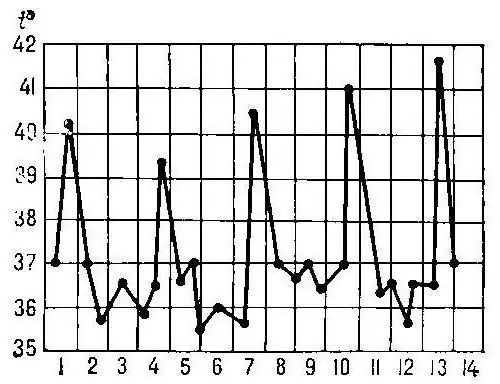
Tilt angle
It is easy to determine from the figure how the derivative of a function changes. If the straight lines of the graph go up over time, then it is positive. And the steeper they are, the greater the value of the derivative, as the angle of inclination increases. During periods of decrease, this value takes negative values, turning to zero at extremum points, and the graph of the derivative in the latter case is drawn parallel to the OX axis.
Any other process should be treated in the same way. But the best thing about this concept can tell the movement of various bodies, clearly shown on the graphs.
Movement
Suppose some object moves in a straight line, gaining speed evenly. During this period, the change in the coordinate of the body graphically represents a certain curve, which a mathematician would call a branch of a parabola. At the same time, the function is constantly increasing, since the coordinate indicators change faster and faster with every second. The speed graph shows the behavior of the derivative, the value of which also increases. This means that the movement has no critical points.
It would have continued indefinitely. But if the body suddenly decides to slow down, stop and start moving in anotherdirection? In this case, the coordinate indicators will begin to decrease. And the function will pass the critical value and turn from increasing to decreasing.

In this example, you can again understand that the extremum points on the function graph appear at the moments when it ceases to be monotonous.
Physical meaning of the derivative
Described earlier clearly showed that the derivative is essentially the rate of change of the function. This refinement contains its physical meaning. Extreme points are critical areas on the chart. It is possible to find out and detect them by calculating the value of the derivative, which turns out to be equal to zero.
There is another sign, which is a sufficient condition for an extremum. The derivative in such places of inflection changes its sign: from "+" to "-" in the region of maximum and from "-" to "+" in the region of minimum.

Movement under the influence of gravity
Let's imagine another situation. The children, playing ball, threw it in such a way that it began to move at an angle to the horizon. At the initial moment, the speed of this object was the largest, but under the influence of gravity it began to decrease, and with each second by the same value, equal to approximately 9.8 m/s2. This is the value of the acceleration that occurs under the influence of the earth's gravity during free fall. On the Moon, it would be about six times smaller.
The graph describing the movement of the body is a parabola with branches,downward. How to find extremum points? In this case, this is the vertex of the function, where the speed of the body (ball) takes on a zero value. The derivative of the function becomes zero. In this case, the direction, and hence the value of the speed, changes to the opposite. The body flies downward with every second faster and faster, and accelerates by the same amount - 9.8 m/s2.
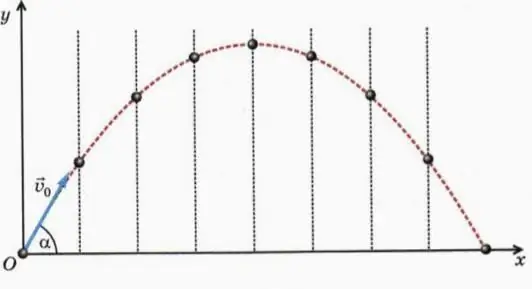
Second derivative
In the previous case, the graph of the velocity modulus is drawn as a straight line. This line is first directed downwards, since the value of this quantity is constantly decreasing. Having reached zero at one of the points in time, then the indicators of this value begin to increase, and the direction of the graphical representation of the speed module changes dramatically. The line is now pointing up.
Velocity, being the time derivative of the coordinate, also has a critical point. In this region, the function, initially decreasing, begins to increase. This is the place of the extremum point of the derivative of the function. In this case, the slope of the tangent becomes zero. And acceleration, being the second derivative of the coordinate with respect to time, changes sign from “-” to “+”. And the movement from uniformly slow becomes uniformly accelerated.
Acceleration chart
Now consider four pictures. Each of them displays a graph of the change over time of such a physical quantity as acceleration. In the case of "A", its value remains positive and constant. This means that the speed of the body, like its coordinate, is constantly increasing. If aimagine that the object will move in this way for an infinitely long time, the function reflecting the dependence of the coordinate on time will turn out to be constantly increasing. It follows from this that it has no critical regions. There are also no extremum points on the graph of the derivative, that is, linearly changing speed.
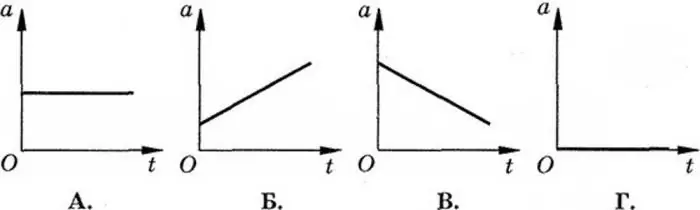
The same applies to case "B" with a positive and constantly increasing acceleration. True, the plots for coordinates and speed will be somewhat more complicated here.
When acceleration tends to zero
Viewing the picture "B", you can see a completely different picture that characterizes the movement of the body. Its speed will be graphically depicted as a parabola with branches pointing downwards. If we continue the line describing the change in acceleration until it intersects with the OX axis, and further, then we can imagine that up to this critical value, where the acceleration turns out to be equal to zero, the speed of the object will increase more and more slowly. The extremum point of the derivative of the coordinate function will be just at the top of the parabola, after which the body will radically change the nature of the movement and begin to move in the other direction.
In the latter case, "G", the nature of the movement cannot be precisely determined. Here we only know that there is no acceleration for some period under consideration. This means that the object can remain in place or the movement occurs at a constant speed.
Coordinate addition task
Let's move on to tasks that are often found in the study of algebra at school and are offered forpreparation for the exam. The figure below shows the graph of the function. It is required to calculate the sum of extremum points.
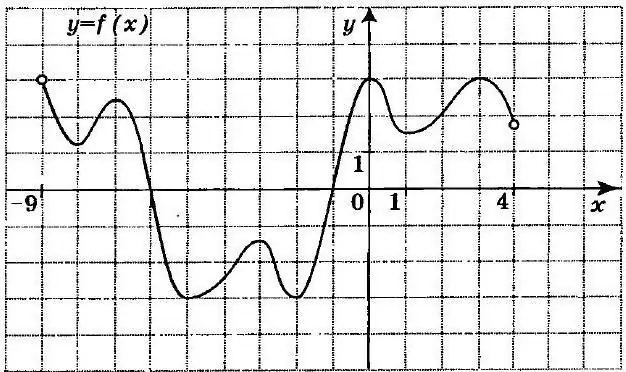
Let's do this for the y-axis by determining the coordinates of critical regions where a change in the characteristics of the function is observed. Simply put, we find the values along the x-axis for the inflection points, and then proceed to add the resulting terms. According to the graph, it is obvious that they take the following values: -8; -7; -5; -3; -2; one; 3. This adds up to -21, which is the answer.
Optimal solution
It is not necessary to explain how important the choice of the optimal solution can be in the performance of practical tasks. After all, there are many ways to achieve the goal, and the best way out, as a rule, is only one. This is extremely necessary, for example, when designing ships, spacecraft and aircraft, architectural structures to find the optimal shape of these man-made objects.
The speed of vehicles largely depends on the competent minimization of the resistance they experience when moving through water and air, from overloads arising under the influence of gravitational forces and many other indicators. A ship at sea needs such qualities as stability during a storm; for a river ship, a minimum draft is important. When calculating the optimal design, the extremum points on the graph can visually give an idea of the best solution to a complex problem. Tasks of this kind are oftenare solved in the economy, in economic areas, in many other life situations.
From ancient history
Extreme problems occupied even the ancient sages. Greek scientists successfully unraveled the mystery of areas and volumes through mathematical calculations. They were the first to understand that on a plane of various figures with the same perimeter, the circle always has the largest area. Similarly, the ball is endowed with the maximum volume among other objects in space with the same surface area. Such famous personalities as Archimedes, Euclid, Aristotle, Apollonius devoted themselves to solving such problems. Heron succeeded very well in finding extremum points, who, having resorted to calculations, built ingenious devices. These included automatic machines moving by means of steam, pumps and turbines operating on the same principle.

Construction of Carthage
There is a legend, the plot of which is based on solving one of the extreme problems. The result of the business approach demonstrated by the Phoenician princess, who turned to the sages for help, was the construction of Carthage. The land plot for this ancient and famous city was presented to Dido (that was the name of the ruler) by the leader of one of the African tribes. The area of the allotment did not seem to him at first very large, since according to the contract it had to be covered with an oxhide. But the princess ordered her soldiers to cut it into thin strips and make a belt out of them. It turned out to be so long that it covered the site,where the whole city fit in.
The origins of calculus
And now let's move from ancient times to a later era. Interestingly, in the 17th century, Kepler was prompted to understand the foundations of mathematical analysis by a meeting with a wine seller. The merchant was so well versed in his profession that he could easily determine the volume of the drink in the barrel by simply lowering an iron tourniquet into it. Reflecting on such a curiosity, the famous scientist managed to solve this dilemma for himself. It turns out that skillful coopers of those times got the hang of making vessels in such a way that at a certain height and radius of the circumference of the fastening rings they would have a maximum capacity.
This was for Kepler reason for further reflection. Bochars came to the optimal solution through a long search, mistakes and new attempts, passing their experience from generation to generation. But Kepler wanted to speed up the process and learn how to do the same in a short time through mathematical calculations. All his developments, picked up by colleagues, turned into the now known theorems of Fermat and Newton - Leibniz.
Maximum area problem
Let's imagine that we have a wire with a length of 50 cm. How to make a rectangle out of it with the largest area?
Starting a decision, one should proceed from simple and known truths. It is clear that the perimeter of our figure will be 50 cm. It also consists of twice the lengths of both sides. This means that, having designated one of them as "X", the other can be expressed as (25 - X).
From here we getan area equal to X (25 - X). This expression can be represented as a function that takes on many values. The solution of the problem requires finding the maximum of them, which means that you should find out the extremum points.
To do this, we find the first derivative and equate it to zero. The result is a simple equation: 25 - 2X=0.
From it we learn that one of the sides X=12, 5.
Therefore, another: 25 - 12, 5=12, 5.
It turns out that the solution to the problem will be a square with a side of 12.5 cm.
How to find the maximum speed
Let's consider one more example. Imagine that there is a body whose rectilinear motion is described by the equation S=- t3 + 9t2 - 24t - 8, where the distance traveled is expressed in meters, and the time is in seconds. It is required to find the maximum speed. How to do it? Downloaded find the speed, that is, the first derivative.
We get the equation: V=- 3t2 + 18t - 24. Now, to solve the problem, we again need to find the extremum points. This must be done in the same way as in the previous task. Find the first derivative of the speed and equate it to zero.
We get: - 6t + 18=0. Hence t=3 s. This is the time when the speed of the body takes on a critical value. We substitute the obtained data into the velocity equation and get: V=3 m/s.
But how to understand that this is exactly the maximum speed, because the critical points of the function can be its maximum or minimum values? To check, you need to find a secondderivative of speed. It is expressed as the number 6 with a minus sign. This means that the found point is the maximum. And in the case of a positive value of the second derivative, there would be a minimum. So, the found solution turned out to be correct.
The tasks given as an example are only a part of those that can be solved by knowing how to find the extremum points of a function. In fact, there are many more. And such knowledge opens up unlimited possibilities for human civilization.






