Volume is a physical quantity that is inherent in a body with non-zero dimensions along each of the three directions of space (all real objects). The article considers the corresponding expression for a cylinder as an example of the volume formula.
Volume of bodies
This physical quantity shows what part of the space is occupied by this or that body. For example, the volume of the Sun is much larger than this value for our planet. This means that the space belonging to the Sun, in which the substance of this star (plasma) is located, exceeds the terrestrial spatial region.
Volume is measured in cubic units of length, in SI it is meters cubed (m3). In practice, the volumes of liquid bodies are measured in liters. Small volumes can be expressed in cubic centimeters, milliliters and other units.
To calculate the volume, the formula will depend on the geometric features of the object in question. For example, for a cube, this is the triple product of the length of its edges. Below we will consider the figure of a cylinder and answer the question of how to find its volume.
Cylinder concept
The figure in question isis quite difficult. According to the geometric definition, it is a surface formed by parallel displacement of a straight line (generatrix) along some curve (directrix). The generatrix is also called the generatrix, and the directrix is also called the guide.
If the directrix is a circle and the generatoratrix is perpendicular to it, then the resulting cylinder is called round and straight. It will be discussed further.
A cylinder has two bases that are parallel to each other and connected by a cylindrical surface. The straight line passing through the centers of the two bases is called the axis of the circular cylinder. All points of the figure are at the same distance from this line, which is equal to the radius of the base.
A round straight cylinder is uniquely defined by two parameters: the radius of the base (R) and the distance between the bases - the height H.
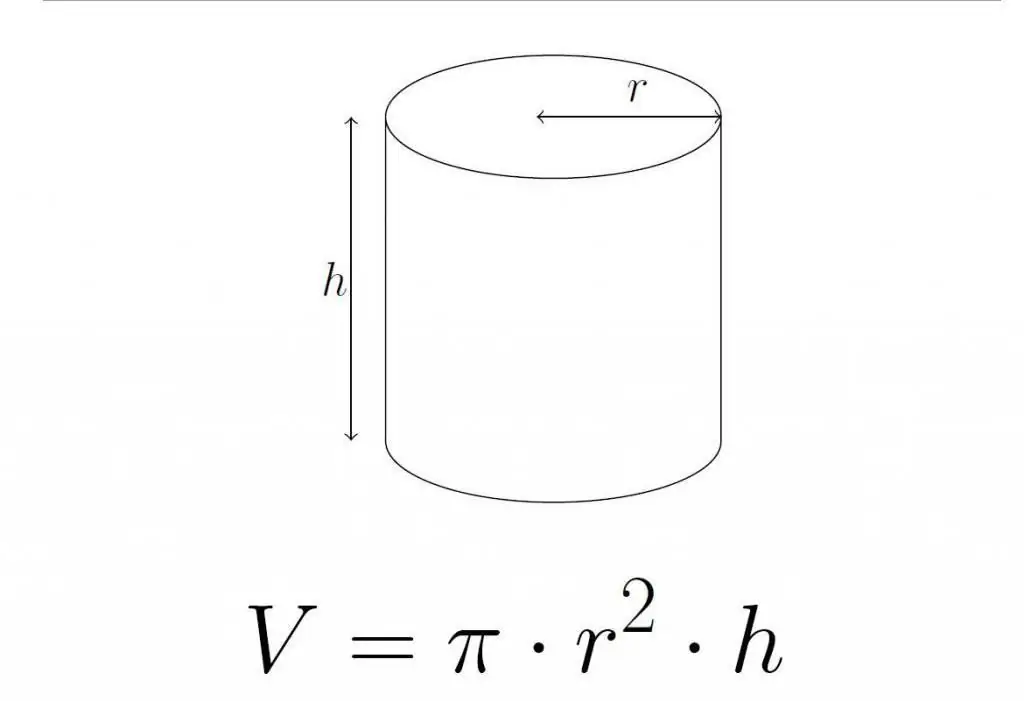
Cylinder volume formula
To calculate the area of space occupied by a cylinder, it is enough to know its height H and base radius R. The required equality in this case looks like:
V=piR2H, here pi=3, 1416
Understanding this volume formula is simple: since the height is perpendicular to the bases, if you multiply it by the area of one of them, you get the desired value V.
Calculation of barrel volume
For example, let's solve the following problem: determine how much water will fit in a barrel with a bottom diameter of 50 cm and a height of 1 meter.

The radius of the barrel is R=D/2=50/2=25 cm. We substitute the data into the formula, we get:
V=piR2H=3, 1416252100=196350 cm 3
Since 1 l=1 dm3=1000 cm3, we get:
V=196350/1000=196.35 liters.
That is, almost 200 liters of water can be poured into a barrel.






