Everyone paid attention to all the variety of types of movement that he encounters in his life. However, any mechanical movement of the body is reduced to one of two types: linear or rotational. Consider in the article the basic laws of motion of bodies.
What types of movement are we talking about?
As noted in the introduction, all types of body motion considered in classical physics are associated either with a rectilinear trajectory or with a circular one. Any other trajectories can be obtained by combining these two. Further in the article, the following laws of body motion will be considered:
- Uniform in a straight line.
- Equivalently accelerated (equally slow) in a straight line.
- Uniform around the circumference.
- Uniformly accelerated around the circumference.
- Move along an elliptical path.
Uniform movement, or state of rest
Galileo first became interested in this movement from a scientific point of view at the end of the 16th - beginning of the 17th century. Studying the inertial properties of the body, as well as introducing the concept of a reference system, he guessed that the state of rest anduniform motion is the same thing (it all depends on the choice of the object relative to which the speed is calculated).
Subsequently, Isaac Newton formulated his first law of motion of a body, according to which the speed of the body is constant whenever there are no external forces that change the characteristics of motion.

Uniform rectilinear movement of a body in space is described by the following formula:
s=vt
Where s is the distance that the body will cover in time t, moving at speed v. This simple expression is also written in the following forms (it all depends on the quantities that are known):
v=s / t; t=s / v
Move in a straight line with acceleration
According to Newton's second law, the presence of an external force acting on a body inevitably leads to the acceleration of the latter. From the definition of acceleration (rate of change of speed) follows the expression:
a=v / t or v=at
If the external force acting on the body remains constant (does not change the module and direction), then the acceleration will not change either. This type of movement is called uniformly accelerated, where acceleration acts as a proportionality factor between speed and time (speed grows linearly).
For this movement, the distance traveled is calculated by integrating speed over time. The law of motion of a body for a path with uniformly accelerated movement takes the form:
s=at2 / 2
The most common example of this movement is the fall of any object from a height, in which gravity gives it an acceleration g=9.81 m/s2.
Rectilinear accelerated (slow) movement with initial speed
In fact, we are talking about a combination of the two types of movement discussed in the previous paragraphs. Imagine a simple situation: a car was driving at a certain speed v0, then the driver applied the brakes and the vehicle stopped after a while. How to describe the movement in this case? For the function of speed versus time, the expression is true:
v=v0 - at
Here v0 is the initial speed (before braking the car). The minus sign indicates that the external force (sliding friction) is directed against the speed v0.

As in the previous paragraph, if we take the time integral of v(t), we get the formula for the path:
s=v0 t - at2 / 2
Note that this formula calculates only the braking distance. To find out the distance traveled by the car for the entire time of its movement, you should find the sum of two paths: for uniform and for uniformly slow motion.
In the example described above, if the driver pressed not the brake pedal, but the gas pedal, then the "-" sign would change to "+" in the presented formulas.
Circular movement
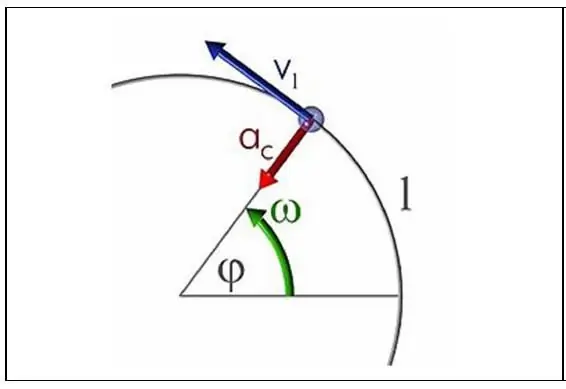
Any movement along a circle cannot occur without acceleration, because even with the preservation of the speed module, its direction changes. The acceleration associated with this change is called centripetal (it is this acceleration that bends the trajectory of the body, turning it into a circle). The module of this acceleration is calculated as follows:
ac=v2 / r, r - radius
In this expression, the speed may depend on time, as it happens in the case of uniformly accelerated motion in a circle. In the latter case, ac will grow rapidly (quadratic dependence).
Centripetal acceleration determines the force that must be applied to keep the body in a circular orbit. An example is the hammer throw competition, where athletes put in a lot of effort to spin the projectile before throwing it.

Rotation around an axis at a constant speed
This type of movement is identical to the previous one, only it is customary to describe it not using linear physical quantities, but using angular characteristics. The law of rotational motion of the body, when the angular velocity does not change, is written in scalar form as follows:
L=Iω
Here L and I are the moments of momentum and inertia, respectively, ω is the angular velocity, which is related to the linear velocity by the equality:
v=ωr
The value ω shows how many radians the body will turn in a second. The quantities L and I have the samemeaning, like momentum and mass for rectilinear motion. Accordingly, the angle θ, by which the body will turn in time t, is calculated as follows:
θ=ωt
An example of this type of movement is the rotation of the flywheel located on the crankshaft in a car engine. The flywheel is a massive disk that is very difficult to give any acceleration. Thanks to this, it provides a smooth change in torque, which is transmitted from the engine to the wheels.

Rotation around an axis with acceleration
If an external force is applied to a system that is capable of rotating, it will begin to increase its angular velocity. This situation is described by the following law of motion of the body around the axis of rotation:
Fd=Idω / dt
Here F is an external force that is applied to the system at a distance d from the axis of rotation. The product on the left side of the equation is called the moment of force.
For uniformly accelerated motion in a circle, we get that ω depends on time as follows:
ω=αt, where α=Fd / I - angular acceleration
In this case, the angle of rotation in time t can be determined by integrating ω over time, i.e.:
θ=αt2 / 2
If the body was already rotating at a certain speed ω0, and then the external moment of force Fd began to act, then by analogy with the linear case, we can write the following expressions:
ω=ω0+ αt;
θ=ω0 t + αt2 / 2
Thus, the appearance of an external moment of forces is the reason for the presence of acceleration in a system with an axis of rotation.
For the sake of completeness, we note that it is possible to change the rotation speed ω not only with the help of the external moment of forces, but also due to a change in the internal characteristics of the system, in particular, its moment of inertia. This situation was seen by every person who watched the rotation of the skaters on the ice. By grouping, athletes increase ω by decreasing I, according to a simple law of body movement:
Iω=const
Movement along an elliptical trajectory on the example of the planets of the solar system

As you know, our Earth and other planets of the solar system revolve around their star not in a circle, but in an elliptical trajectory. For the first time, the famous German scientist Johannes Kepler formulated mathematical laws to describe this rotation at the beginning of the 17th century. Using the results of his teacher Tycho Brahe's observations of the motion of the planets, Kepler came to the formulation of his three laws. They are worded as follows:
- The planets of the solar system move in elliptical orbits, with the Sun located at one of the foci of the ellipse.
- The radius-vector that connects the Sun and the planet describes the same areas in equal time intervals. This fact follows from the conservation of angular momentum.
- If we divide the square of the periodrevolution on the cube of the semi-major axis of the elliptical orbit of the planet, then a certain constant is obtained, which is the same for all the planets of our system. Mathematically, this is written as follows:
T2 / a3=C=const
Subsequently, Isaac Newton, using these laws of motion of bodies (planets), formulated his famous law of universal gravity, or gravitation. Using it, we can show that the constant C in Kepler's 3rd law is:
C=4pi2 / (GM)
Where G is the gravitational universal constant and M is the mass of the Sun.
Note that the movement along an elliptical orbit in the case of the action of the central force (gravity) leads to the fact that the linear velocity v is constantly changing. It is maximum when the planet is closest to the star, and minimum away from it.






