Movement is one of the main features of the world we live in. It is known from physics that all bodies and the particles of which they are composed are constantly moving in space even at absolute zero temperatures. In this article, we will consider the definition of acceleration as an important kinematic characteristic of mechanical motion in physics.
What size are we talking about?
According to the definition, acceleration is a quantity that allows you to quantitatively describe the process of changing speed with time. Mathematically, acceleration is calculated as follows:
a¯=dv¯/dt.
This formula for determining acceleration describes the so-called instantaneous value a¯. To calculate the average acceleration, you should take the ratio of the difference in speeds to a longer period of time.
The value a¯ is a vector. If the velocity is directed along the tangent to the considered trajectory of the body, then the acceleration can bedirected in a completely random way. It has nothing to do with the trajectory of movement and with the vector v¯. Nevertheless, both named characteristics of motion depend on acceleration. This is because, ultimately, it is the acceleration vector that determines the trajectory and speed of the body.
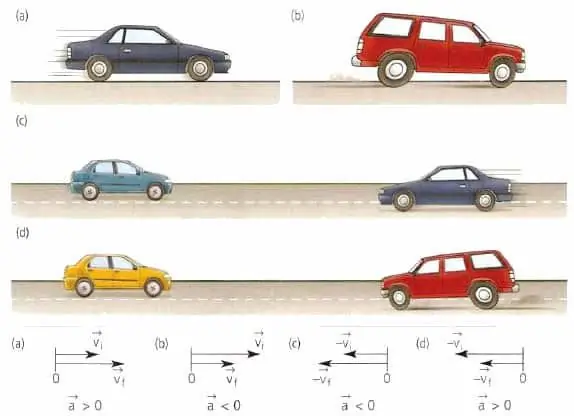
To understand where the acceleration a¯ is directed, one should write down Newton's second law. In the well-known form, it looks like this:
F¯=ma¯.
Equality says that two vectors (F¯ and a¯) are related to each other through a numerical constant (m). It is known from the properties of vectors that multiplication by a positive number does not change the direction of the vector. In other words, the acceleration is always directed towards the action of the total force F¯ on the body.
The quantity under consideration is measured in meters per square second. For example, the gravitational force of the Earth near its surface imparts to bodies an acceleration of 9.81 m/s2, that is, the speed of a freely falling body in airless space increases by 9.81 m/s every second.
The concept of uniformly accelerated motion
The formula for determining acceleration in the general case was written above. However, in practice it is often necessary to solve problems for the so-called uniformly accelerated motion. It is understood as such a movement of bodies in which their tangential component of acceleration is a constant value. We emphasize the importance of the constancy of the tangential, and not the normal component of acceleration.

Total acceleration of the body in the process of curvilinear motion can be represented as two components. The tangential component describes the change in the velocity modulus. The normal component is always directed perpendicular to the trajectory. It does not change the speed modulus, but it does change its vector.
Below, we will cover the question regarding the acceleration component in more detail.
Motion uniformly accelerated in a straight line
Since the velocity vector does not change when moving in a straight line of the body, the normal acceleration is zero. This means that the total acceleration is formed exclusively by the tangential component. The definition of acceleration during uniformly accelerated motion is carried out according to the following formulas:
a=(v - v0)/t;
a=2S/t2;
a=2(S-v0t)/t2.
These three equations are the basic expressions of kinematics. Here v0 is the speed that the body had before the acceleration. It's called initial. The value S is the path traveled by the body along a straight trajectory during the time t.
Whatever value of time t we substitute into any of these equations, we will always get the same acceleration a, since it does not change during the considered type of movement.
Fast spin
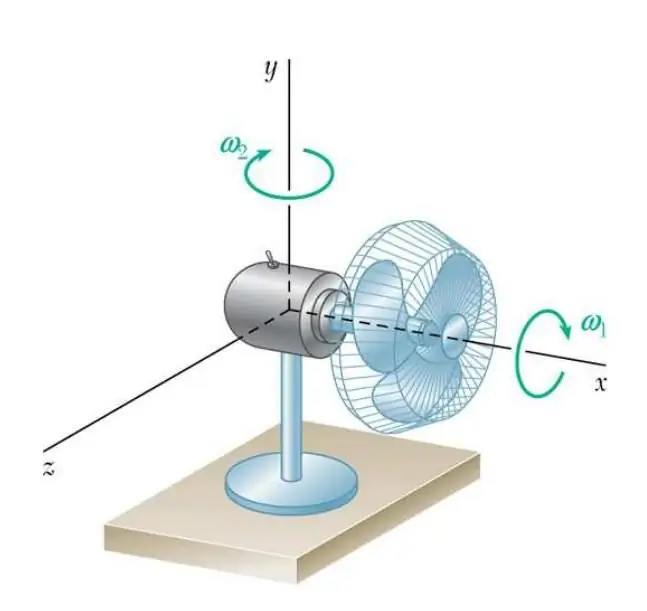
Moving around a circle with acceleration is a fairly common type of movement in technology. To understand this, it is enough to recall the rotation of the shafts,disks, wheels, bearings. To determine the acceleration of a body during uniformly accelerated motion in a circle, not linear quantities are often used, but angular ones. Angular acceleration, for example, is defined as follows:
α=dω/dt.
The value of α is expressed in radians for every second squared. This acceleration with the tangential component of the quantity a is related as follows:
α=at/r.
Since α is constant during uniformly accelerated rotation, the tangential acceleration at increases in direct proportion with increasing rotation radius r.

If α=0, then there is only non-zero normal acceleration during rotation. However, this movement is called uniformly variable or uniform rotation, not uniformly accelerated.






