Modulus of elasticity is a physical quantity that characterizes the elastic behavior of a material when an external force is applied to it in a particular direction. The elastic behavior of a material means its deformation in the elastic region.
History of the study of elasticity of materials

The physical theory of elastic bodies and their behavior under the action of external forces was considered in detail and studied by the English scientist of the 19th century, Thomas Young. However, the very concept of elasticity was developed back in 1727 by the Swiss mathematician, physicist and philosopher Leonhard Euler, and the first experiments related to the modulus of elasticity were carried out in 1782, that is, 25 years before the work of Thomas Jung, by the Venetian mathematician and philosopher Jacopo Ricatti.
Thomas Young's merit lies in the fact that he gave the theory of elasticity a slender modern look, which was subsequently formalized in the form of a simple and then generalized Hooke's law.
Physical nature of elasticity
Any body consists of atoms, between which the forces of attraction and repulsion act. The balance of these forces isthe state and parameters of matter under given conditions. The atoms of a solid body, when insignificant external forces of tension or compression are applied to them, begin to shift, creating a force opposite in direction and equal in magnitude, which tends to return the atoms to their initial state.
In the process of such displacement of atoms, the energy of the entire system increases. Experiments show that at small strains the energy is proportional to the square of these strains. This means that the force, being a derivative with respect to energy, turns out to be proportional to the first power of the strain, that is, it depends linearly on it. Answering the question, what is the modulus of elasticity, we can say that this is the coefficient of proportionality between the force acting on the atom and the deformation that this force causes. The dimension of Young's modulus is the same as the dimension of pressure (Pascal).
Elastic limit
According to the definition, the modulus of elasticity indicates how much stress must be applied to a solid in order for its deformation to be 100%. However, all solids have an elastic limit equal to 1% strain. This means that if an appropriate force is applied and the body is deformed by an amount less than 1%, then after the termination of this force, the body exactly restores its original shape and dimensions. If too much force is applied, at which the deformation value exceeds 1%, after the termination of the external force, the body will no longer restore its original dimensions. In the latter case, one speaks of the existence of a residual deformation, which isevidence that the elastic limit of the material has been exceeded.
Young's modulus in action
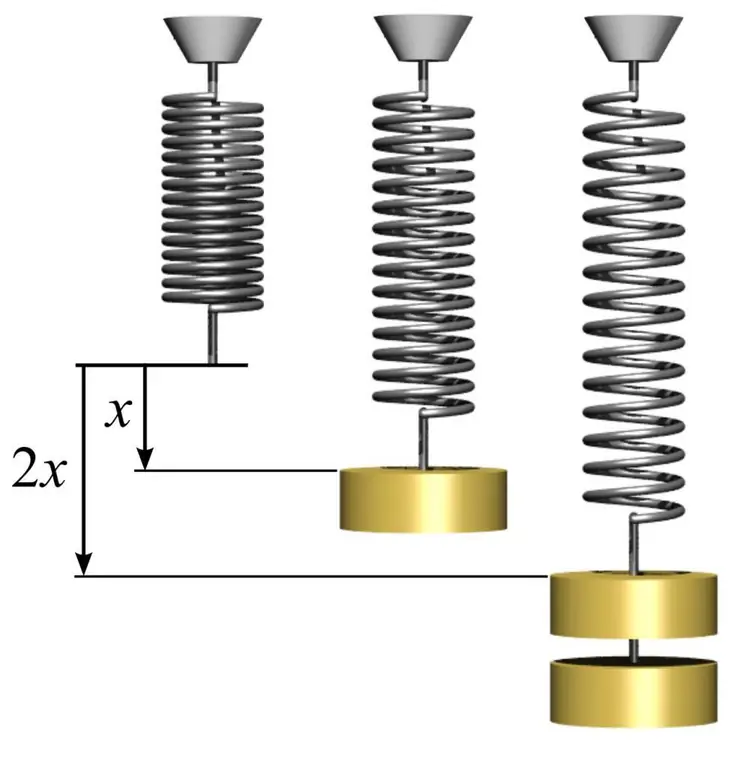
To determine the modulus of elasticity, as well as to understand how to use it, you can give a simple example with a spring. To do this, you need to take a metal spring and measure the area of \u200b\u200bthe circle that its coils form. This is done using the simple formula S=πr², where n is pi equal to 3.14 and r is the radius of the coil of the spring.
Next, measure the length of the spring l0 without load. If you hang any load of mass m1 on a spring, then it will increase its length to a certain value l1. The modulus of elasticity E can be calculated based on the knowledge of Hooke's law by the formula: E=m1gl0/(S(l 1-l0)), where g is the free fall acceleration. In this case, we note that the amount of deformation of the spring in the elastic region can greatly exceed 1%.
Knowing Young's modulus allows you to predict the amount of deformation under the action of a particular stress. In this case, if we hang another mass m2 on the spring, we get the following value of relative deformation: d=m2g/(SE), where d - relative deformation in the elastic region.
Isotropy and anisotropy
Modulus of elasticity is a characteristic of a material that describes the strength of the bond between its atoms and molecules, however a particular material can have several different Young's moduli.
The fact is that the properties of each solid depend on its internal structure. If the properties are the same in all spatial directions, then we are talking about an isotropic material. Such substances have a homogeneous structure, so the action of an external force in different directions on them causes the same reaction from the material. All amorphous materials are isotropic, such as rubber or glass.
Anisotropy is a phenomenon that is characterized by the dependence of the physical properties of a solid or liquid on direction. All metals and alloys based on them have one or another crystal lattice, that is, an ordered, rather than a chaotic arrangement of ionic cores. For such materials, the modulus of elasticity varies depending on the axis of action of the external stress. For example, metals with cubic symmetry, such as aluminum, copper, silver, refractory metals, and others, have three different Young's moduli.
Shear modulus
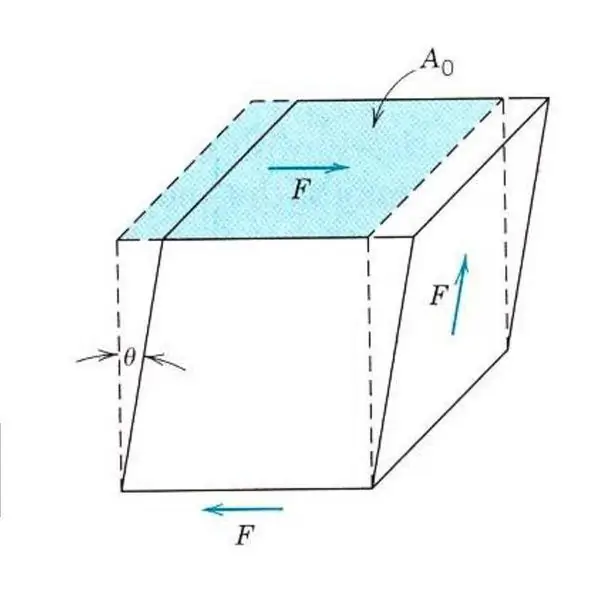
Description of the elastic properties of even an isotropic material does not require knowledge of one Young's modulus. Because, in addition to tension and compression, the material can be affected by shear stresses or torsional stresses. In this case, it will react differently to external force. To describe elastic shear deformation, an analogue of Young's modulus, shear modulus, or modulus of elasticity of the second kind is introduced.
All materials resist shear stresses less than tension or compression, so the shear modulus value for them is 2-3 times less than the value of Young's modulus. Thus, for titanium, whose Young's modulus is equal to 107 GPa, the shear modulus isonly 40 GPa, for steel these figures are 210 GPa and 80 GPa, respectively.
Modulus of elasticity of wood

Wood is an anisotropic material because wood fibers are oriented along a specific direction. It is along the fibers that the modulus of elasticity of wood is measured, since it is 1-2 orders of magnitude smaller across the fibers. Knowledge of Young's modulus for wood is important and is taken into account when designing wood panel structures.
The values of the modulus of elasticity of wood for some types of trees are shown in the table below.
| Tree view | Young's modulus in GPa |
| Laurel tree | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Oak | 12 |
It should be noted that the values given may differ by up to 1 GPa for a particular tree, since its Young's modulus is affected by the density of the wood and growing conditions.

Shear moduli for various tree species are in the range of 1-2 GPa, for example, for pine it is 1.21 GPa, and for oak 1.38 GPa, that is, wood practically does not resist shear stresses. This fact must be taken into account in the manufacture of wooden load-bearing structures, which are designed to work only in tension or compression.
Elastic characteristics of metals
When compared with the Young's modulus of wood, the average values of this value for metals and alloys are an order of magnitude greater, as shown in the following table.
| Metal | Young's modulus in GPa |
| Bronze | 120 |
| Copper | 110 |
| Steel | 210 |
| Titanium | 107 |
| Nickel | 204 |
Elastic properties of metals that have a cubic syngony are described by three elastic constants. Such metals include copper, nickel, aluminum, iron. If a metal has a hexagonal syngony, then six constants are already needed to describe its elastic characteristics.
For metallic systems, Young's modulus is measured within 0.2% strain, as large values can already occur in the inelastic region.






