Rotational dynamics is one of the important branches of physics. It describes the reasons for the movement of bodies in a circle around a certain axis. One of the important quantities of the dynamics of rotation is the moment of force, or torque. What is a moment of force? Let's explore this concept in this article.
What should you know about the rotation of bodies?
Before giving an answer to the question what is the moment of force, let's characterize the process of rotation from the point of view of physical geometry.
Each person intuitively imagines what is at stake. Rotation implies such a movement of a body in space, when all its points move along circular paths around some axis or point.
Unlike linear movement, rotation process is described by angular physical characteristics. Among them are the angle of rotation θ, the angular velocity ω and the angular acceleration α. The value of θ is measured in radians (rad), ω - in rad/s, α - in rad/s2.
Examples of rotation are the movement of our planet around its star,spinning the engine rotor, the movement of the Ferris wheel and others.
The concept of torque

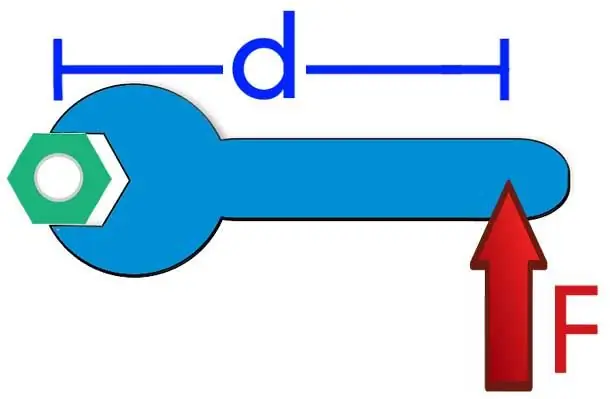
The moment of force is a physical quantity equal to the vector product of the radius vector r¯, directed from the axis of rotation to the point of application of the force F¯, and the vector of this force. Mathematically, this is written like this:
M¯=[r¯F¯].
As you can see, the moment of force is a vector quantity. Its direction is determined by the rule of a gimlet or right hand. The value of M¯ is directed perpendicular to the plane of rotation.
In practice, it often becomes necessary to calculate the absolute value of the moment M¯. To do this, use the following expression:
M=rFsin(φ).
Where φ is the angle between the vectors r¯ and F¯. The product of the modulus of the radius vector r and the sine of the marked angle is called the shoulder of the force d. The latter is the distance between the vector F¯ and the axis of rotation. The formula above can be rewritten as:
M=dF, where d=rsin(φ).
Moment of force is measured in newtons per meter (Nm). However, you should not use joules (1 Nm=1 J) because M¯ is not a scalar, but a vector.
Physical meaning of M¯
The physical meaning of the moment of force is easiest to understand with the following examples:
- We propose to do the following experiment: try to open the door,pushing it near the hinges. To do this operation successfully, you will have to apply a lot of force. At the same time, the handle of any door opens quite easily. The difference between the two cases described is the length of the arm of the force (in the first case, it is very small, so the moment created will also be small and require a large force).
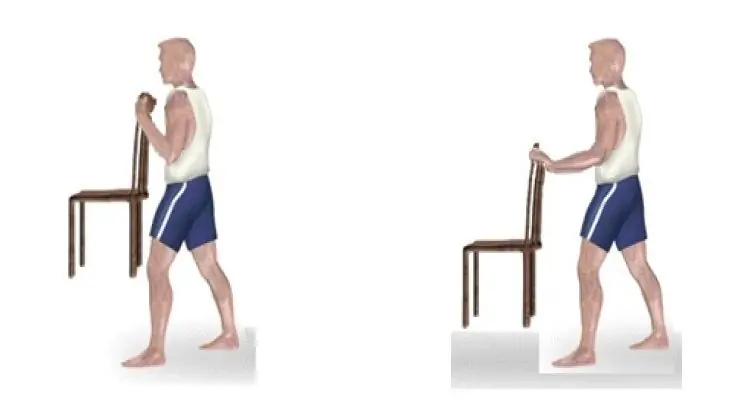
- Another experiment that shows the meaning of torque is as follows: take a chair and try to hold it with your arm outstretched forward in weight. It is quite difficult to do this. At the same time, if you press your hand with a chair to your body, then the task will no longer seem overwhelming.
- Everyone involved in technology knows that it is much easier to unscrew a nut with a wrench than to do it with your fingers.
All these examples speak of one thing: the moment of force reflects the ability of the latter to rotate the system around its axis. The greater the torque, the more likely it will make a turn in the system and give it an angular acceleration.
Torque and balance of bodies
Statics - a section that studies the causes of equilibrium of bodies. If the system under consideration has one or more axes of rotation, then this system can potentially perform circular motion. To prevent this from happening and the system was at rest, the sum of all n external moments of forces relative to any axis must be equal to zero, that is:
∑i=1Mi=0.
When using thisthe conditions for the equilibrium of bodies during the solution of practical problems, it should be remembered that any force tending to rotate the system counterclockwise creates a positive torque, and vice versa.
Obviously, if a force is applied to the axis of rotation, then it will not create any moment (shoulder d is equal to zero). Therefore, the reaction force of the support never creates a moment of force if it is calculated relative to this support.

Example problem
Having figured out how to determine the moment of force, we will solve the following interesting physical problem: suppose that there is a table on two supports. The table is 1.5 meters long and weighs 30 kg. A weight of 5 kg is placed at a distance of 1/3 from the right edge of the table. It is necessary to calculate what reaction force will act on each support of the table with the load.
Calculation of the problem should be carried out in two stages. First, consider a table without a load. Three forces act on it: two identical support reactions and body weight. Since the table is symmetrical, the reactions of the supports are equal to each other and together balance the weight. The value of each support reaction is:
N0=P / 2=mg / 2=309, 81 / 2=147, 15 N.
As soon as the load is placed on the table, the reaction values of the supports change. To calculate them, we use the equilibrium of moments. First, consider the moments of forces acting relative to the left support of the table. There are two of these moments: the additional reaction of the right support without taking into account the weight of the table and the weight of the load itself. Since the system is in equilibrium,get:
ΔN1 l - m1 g2 / 3l=0.
Here l is the length of the table, m1 is the weight of the load. From the expression we get:
ΔN1=m1 g2 / 3=2 / 39, 815=32, 7 N.
In a similar way, we calculate the additional reaction to the left support of the table. We get:
-ΔN2 l + m1 g1/3l=0;
ΔN2=m1 g1 / 3=1 / 359, 81=16, 35 N.
To calculate the reactions of the table supports with a load, you need the values ΔN1 and ΔN2add to N0 , we get:
right support: N1=N0+ ΔN1=147, 15 + 32, 7=179, 85 N;
left support: N2=N0 + ΔN2=147, 15 + 16, 35=163, 50 N.
Thus, the load on the right leg of the table will be greater than on the left.






