What is a cube and what diagonals does it have
Cube (regular polyhedron or hexahedron) is a three-dimensional figure, each face is a square, in which, as we know, all sides are equal. The diagonal of a cube is a segment that passes through the center of the figure and connects symmetrical vertices. A regular hexahedron has 4 diagonals, and they will all be equal. It is very important not to confuse the diagonal of the figure itself with the diagonal of its face or the square that lies on its base. The diagonal of the cube face passes through the center of the face and connects the opposite vertices of the square.
The formula for finding the diagonal of a cube
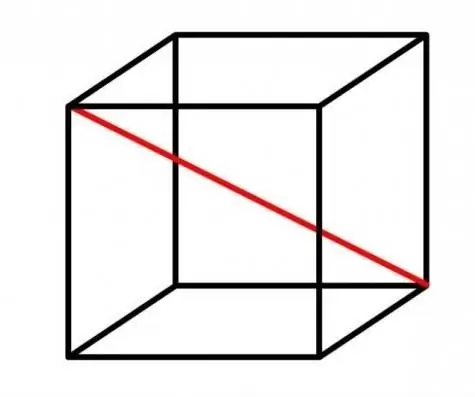
The diagonal of a regular polyhedron can be found using a very simple formula that must be remembered. D=a√3, where D denotes the diagonal of a cube, and is an edge. Let us give an example of a problem where it is necessary to find a diagonal if it is known that the length of its edge is 2 cm. Here everything is simple D=2√3, you don’t even need to count anything. In the second example, let the edge of the cube be √3 cm, then we getD=√3√3=√9=3. Answer: D is 3 cm.
The formula for finding the diagonal of a cube face
Diago
nal faces can also be found by the formula. There are only 12 diagonals that lie on the faces, and they are all equal to each other. Now remember d=a√2, where d is the diagonal of the square, and is also the edge of the cube or the side of the square. It is very easy to understand where this formula came from. After all, the two sides of the square and the diagonal form a right triangle. In this trio, the diagonal plays the role of the hypotenuse, and the sides of the square are the legs, which have the same length. Recall the Pythagorean theorem, and everything will immediately fall into place. Now the problem: the edge of the hexahedron is √8 cm, you need to find the diagonal of its face. We insert into the formula, and we get d=√8 √2=√16=4. Answer: the diagonal of the face of the cube is 4 cm.
If the diagonal of the cube face is known
According to the condition of the problem, we are given only the diagonal of the face of a regular polyhedron, which is equal to, say, √2 cm, and we need to find the diagonal of the cube. The formula for solving this problem is slightly more complicated than the previous one. If we know d, then we can find the edge of the cube based on our second formula d=a√2. We get a=d/√2=√2/√2=1cm (this is our edge). And if this value is known, then it will not be difficult to find the diagonal of the cube: D=1√3=√3. This is how we solved our problem.
If the surface area is known

Nextthe solution algorithm is based on finding the diagonal along the surface area of the cube. Suppose it is 72cm2. First, let's find the area of one face, and there are 6 in total. So, 72 must be divided by 6, we get 12 cm2. This is the area of one face. To find the edge of a regular polyhedron, you need to remember the formula S=a2, so a=√S. Substitute and get a=√12 (cube edge). And if we know this value, then it is not difficult to find the diagonal D=a√3=√12 √3=√36=6. Answer: the diagonal of a cube is 6 cm2.
If the length of the edges of the cube is known
There are cases when only the length of all cube edges is given in the problem. Then you need to divide this value by 12. That is how many sides are in a regular polyhedron. For example, if the sum of all edges is 40, then one side will be equal to 40/12=3, 333. Insert into our first formula and get the answer!






