Knowing the definitions in physics is a key factor for successfully solving various physical problems. In the article, we will consider what is meant by isobaric, isochoric, isothermal and adiabatic processes for an ideal gas system.
Ideal gas and its equation
Before proceeding to the description of isobaric, isochoric and isothermal processes, let's consider what an ideal gas is. Under this definition in physics they consider a system consisting of a huge number of dimensionless and non-interacting particles that move at high speeds in all directions. In fact, we are talking about a gaseous aggregate state of matter, in which the distances between atoms and molecules far exceed their sizes and in which the potential energy of interaction of particles is neglected due to its smallness, compared to the kinetic energy.
The state of an ideal gas is the totality of its thermodynamic parameters. The main ones are temperature, volume and pressure. Let's denote them by the letters T, V and P, respectively. In the 30s of the XIX centuryClapeyron (a French scientist) first wrote down an equation that combines the indicated thermodynamic parameters within a single equality. It looks like:
PV=nRT,
where n and R are the quantity of substances and the gas constant, respectively.
What are isoprocesses in gases?
As many have noticed, isobaric, isochoric and isothermal processes use the same "iso" prefix in their names. It means the equality of one thermodynamic parameter during the passage of the entire process, while the remaining parameters change. For example, an isothermal process indicates that, as a result, the absolute temperature of the system is maintained constant, while an isochoric process indicates a constant volume.
Isoprocesses are convenient to study, since fixing one of the thermodynamic parameters leads to a simplification of the general equation of gas state. It is important to note that the gas laws for all these isoprocesses were discovered experimentally. Their analysis allowed Clapeyron to obtain the reduced universal equation.
Isobaric, isochoric and isothermal processes
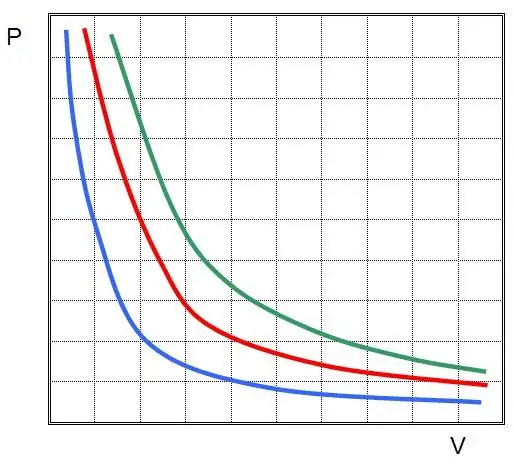
The first law was discovered for an isothermal process in an ideal gas. Now it is called the Boyle-Mariotte law. Since T does not change, the equation of state implies the equality:
PV=const.
In other words, any change in pressure in the system leads to an inversely proportional change in its volume, if the temperature of the gas is maintained constant. The graph of the function P(V) ishyperbole.
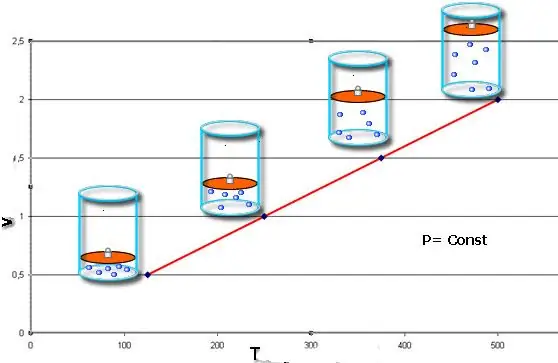
Isobaric process - this is a change in the state of the system, in which the pressure remains constant. Having fixed the value of P in the Clapeyron equation, we obtain the following law:
V/T=const.
This equality bears the name of the French physicist Jacques Charles, who received it at the end of the 18th century. The isobar (graphic representation of the V(T) function) looks like a straight line. The more pressure in the system, the faster this line rises.
The isobaric process is easy to implement if the gas is heated under the piston. The molecules of the latter increase their speed (kinetic energy), create a higher pressure on the piston, which leads to the expansion of the gas and maintaining a constant value of P.
Finally, the third isoprocess is isochoric. It runs with a constant volume. From the equation of state we obtain the corresponding equality:
P/T=const.
It is known among physicists as Gay-Lussac's law. The direct proportionality between pressure and absolute temperature indicates that the graph of the isochoric process, like the graph of the isobaric, is a straight line with a positive slope.
It is important to understand that all isoprocesses occur in closed systems, that is, the value of n is preserved during their course.
Adiabatic process
This process does not belong to the "iso" category, since all three thermodynamic parameters change during its passage. adiabaticcalled the transition between two states of the system, in which it does not exchange heat with the environment. Thus, the expansion of the system is carried out due to its internal energy reserves, which leads to a significant drop in pressure and absolute temperature in it.
Adiabatic process for an ideal gas is described by Poisson's equations. One of them is shown below:
PVγ=const,
where γ is the ratio of heat capacities at constant pressure and at constant volume.
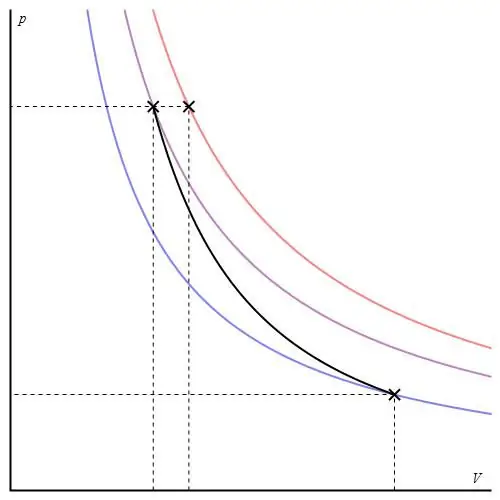
The adiabatic graph differs from the isochoric process graph and from the isobaric graph, but it is similar to a hyperbola (isotherm). The adiabat in the P-V axes behaves more sharply than the isotherm.






