Inequalities and systems of inequalities is one of the topics that is taught in high school algebra. In terms of difficulty, it is not the most difficult, because it has simple rules (about them a little later). As a rule, schoolchildren learn the solution of systems of inequalities quite easily. This is also due to the fact that teachers simply "train" their students on this topic. And they cannot but do this, because it is studied in the future with the use of other mathematical quantities, and is also checked for the OGE and the Unified State Examination. In school textbooks, the topic of inequalities and systems of inequalities is covered in great detail, so if you are going to study it, then it is best to resort to them. This article is only a paraphrase of much material and may contain some omissions.

The concept of a system of inequalities
If we turn to the scientific language, we can define the concept of "systeminequalities". This is such a mathematical model that represents several inequalities. Of course, this model requires a solution, and it will be the general answer for all the inequalities of the system proposed in the task (usually it is written like this, for example: "Solve the system of inequalities 4 x + 1 > 2 and 30 - x > 6… ").

Systems of inequalities and systems of equations
In the process of learning a new topic, misunderstandings often arise. On the one hand, everything is clear and I would rather start solving tasks, but on the other hand, some moments remain in the "shadow", they are not well understood. Also, some elements of already acquired knowledge can be intertwined with new ones. Mistakes often occur as a result of this overlap.
Therefore, before proceeding to the analysis of our topic, we should recall the differences between equations and inequalities, their systems. To do this, you need to explain once again what these mathematical concepts are. An equation is always an equality, and it is always equal to something (in mathematics, this word is denoted by the sign "="). Inequality is a model in which one value is either greater or less than another, or contains the assertion that they are not the same. Thus, in the first case, it is appropriate to speak of equality, and in the second, no matter how obvious it may sound fromthe name itself, about the inequality of the initial data. The systems of equations and inequalities practically do not differ from each other and the methods for their solution are the same. The only difference is that the former uses equalities while the latter uses inequalities.
Types of inequalities
There are two types of inequalities: numerical and with an unknown variable. The first type is provided values (numbers) that are unequal to each other, for example, 8 > 10. The second is inequalities containing an unknown variable (indicated by some letter of the Latin alphabet, most often X). This variable needs to be found. Depending on how many there are, the mathematical model distinguishes between inequalities with one (they make up a system of inequalities with one variable) or several variables (they make up a system of inequalities with several variables).

The last two types, according to the degree of their construction and the level of complexity of the solution, are divided into simple and complex. Simple ones are also called linear inequalities. They, in turn, are divided into strict and non-strict. Strict specifically "say" that one value must be either less or more, so this is pure inequality. There are several examples: 8 x + 9 > 2, 100 - 3 x > 5, etc. Non-strict ones also include equality. That is, one value can be greater than or equal to another value (sign "≧") or less than or equal to another value (sign "≦"). Still in lineIn inequalities, the variable does not stand at the root, square, is not divisible by anything, which is why they are called "simple". Complex ones include unknown variables, the finding of which requires more mathematical operations. They are often in a square, cube or under the root, they can be modular, logarithmic, fractional, etc. But since our task is to understand the solution of systems of inequalities, we will talk about a system of linear inequalities. However, before that, a few words should be said about their properties.
Properties of inequalities
The properties of inequalities include the following provisions:
- The inequality sign is reversed if the operation to change the sequence of sides is applied (for example, if t1 ≦ t2, then t 2 ≧ t1).
- Both parts of the inequality allow you to add the same number to yourself (for example, if t1 ≦ t2, then t 1 + number ≦ t2 + number).
- Two or more inequalities with the sign of the same direction allow you to add their left and right parts (for example, if t1 ≧ t2, t3 ≧ t4, then t1 + t3 ≧ t2 + t4).
- Both parts of the inequality allow themselves to be multiplied or divided by the same positive number (for example, if t1 ≦ t2 and number ≦ 0, then number t1 ≧ number t2).
- Two or more inequalities that have positive terms and a sign of the same direction allowmultiply each other (for example, if t1 ≦ t2, t3 ≦ t 4, t1, t2, t3, t4 ≧ 0 then t1 t3 ≦ t2t4).
- Both parts of the inequality allow themselves to be multiplied or divided by the same negative number, but the inequality sign changes (for example, if t1 ≦ t 2 and number ≦ 0, then number t1 ≧ number t2).
- All inequalities are transitive (for example, if t1 ≦ t2 and t2≦ t3, then t1 ≦ t3).

Now, after studying the main provisions of the theory related to inequalities, we can proceed directly to the consideration of the rules for solving their systems.
Solution of systems of inequalities. General information. Solutions
As mentioned above, the solution is the values of the variable that fit all the inequalities of the given system. The solution of systems of inequalities is the implementation of mathematical operations that ultimately lead to the solution of the entire system or prove that it has no solutions. In this case, the variable is said to refer to the empty number set (written as follows: the letter denoting the variable ∈ (the sign "belongs") ø (the sign "empty set"), for example, x ∈ ø (it is read like this: "The variable "x" belongs to the empty set"). There are several ways to solve systems of inequalities:graphical, algebraic, substitution method. It is worth noting that they refer to those mathematical models that have several unknown variables. In the case where there is only one, the spacing method will do.
Graphic method
Allows you to solve a system of inequalities with several unknowns (from two or more). Thanks to this method, the system of linear inequalities is solved quite easily and quickly, so it is the most common method. This is because plotting reduces the amount of writing mathematical operations. It becomes especially pleasant to take a little break from the pen, pick up a pencil with a ruler and proceed with further actions with their help when a lot of work has been done and you want a little variety. However, some do not like this method due to the fact that you have to break away from the task and switch your mental activity to drawing. However, it is a very effective way.
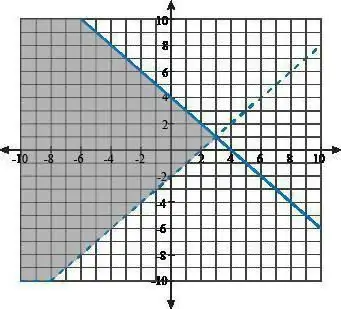
To solve a system of inequalities using a graphical method, it is necessary to transfer all members of each inequality to their left side. The signs will be reversed, zero should be written on the right, then each inequality should be written separately. As a result, functions will be obtained from inequalities. After that, you can get a pencil and a ruler: now you need to draw a graph of each function obtained. The whole set of numbers that will be in the interval of their intersection will be the solution to the system of inequalities.
Algebraic way
Allows you to solve a system of inequalities with two unknown variables. Inequalities must also have the same inequality sign (that is, they must contain either only the "greater than" sign, or only the "less than" sign, etc.) Despite its limitations, this method is also more complicated. It is applied in two steps.
The first one involves getting rid of one of the unknown variables. First you need to select it, then check for the presence of numbers in front of this variable. If there are none (then the variable will look like a single letter), then we do not change anything, if there is (the type of the variable will be, for example, 5y or 12y), then it is necessary to make sure that in each inequality the number in front of the selected variable is the same. To do this, you need to multiply each member of the inequalities by a common factor, for example, if 3y is written in the first inequality, and 5y in the second, then you need to multiply all the members of the first inequality by 5, and the second by 3. You get 15y and 15y, respectively.
The second stage of the decision. It is necessary to transfer the left part of each inequality to their right parts with a change in the sign of each term to the opposite, write zero on the right. Then comes the fun part: getting rid of the chosen variable (otherwise known as "reduction") while adding up the inequalities. You will get an inequality with one variable that needs to be solved. After that, you should do the same, only with another unknown variable. The results obtained will be the solution of the system.
Substitution method
Allows you to solve a system of inequalities when you have the opportunity to introduce a new variable. Usually this method is used when the unknown variable in one term of the inequality is raised to the fourth power, and in the other term it is squared. Thus, this method is aimed at reducing the degree of inequalities in the system. The sample inequality x4 - x2 - 1 ≦ 0 is solved in this way as follows. A new variable is introduced, for example t. They write: "Let t=x2", then the model is rewritten in a new form. In our case, we get t2 - t - 1 ≦0. This inequality needs to be solved by the interval method (about it a little later), then return back to the variable X, then do the same with another inequality. The answers received will be the decision of the system.
Interval method
This is the easiest way to solve systems of inequalities, and at the same time it is universal and widespread. It is used in high school, and even in high school. Its essence lies in the fact that the student is looking for intervals of inequality on the number line, which is drawn in a notebook (this is not a graph, but just an ordinary straight line with numbers). Where the intervals of inequalities intersect, the solution of the system is found. To use the spacing method, follow these steps:
- All members of each inequality are transferred to the left side with a change of sign to the opposite (zero is written on the right).
- Inequalities are written out separately, the solution of each of them is determined.
- The intersections of inequalities on the numericalstraight. All numbers at these intersections will be the solution.
Which way to use?
Obviously the one that seems the easiest and most convenient, but there are times when tasks require a certain method. Most often, they say that you need to solve either using a graph or using the interval method. The algebraic method and substitution are used extremely rarely or not at all, since they are quite complex and confusing, and besides, they are more used for solving systems of equations rather than inequalities, so you should resort to drawing graphs and intervals. They bring visibility, which cannot but contribute to the efficient and fast conduct of mathematical operations.
If something doesn't work
During the study of a particular topic in algebra, of course, there may be problems with its understanding. And this is normal, because our brain is designed in such a way that it is not able to understand complex material in one go. Often you need to reread a paragraph, take the help of a teacher, or practice solving typical problems. In our case, they look, for example, like this: "Solve the system of inequalities 3 x + 1 ≧ 0 and 2 x - 1 > 3". Thus, personal striving, help from outsiders and practice help in understanding any complex topic.

Reshebnik?
And the solution book is also very good, but not for cheating homework, but for self-help. In them you can find systems of inequalities with a solution, look atthem (like templates), try to understand exactly how the author of the solution coped with the task, and then try to do it on his own.
Conclusions
Algebra is one of the hardest subjects in school. Well, what can you do? Mathematics has always been like this: for some it comes easily, and for others it is difficult. But in any case, it should be remembered that the general education program is designed in such a way that any student can cope with it. In addition, you need to keep in mind a huge number of assistants. Some of them have been mentioned above.






