Tangential or tangential acceleration

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

All the bodies that surround us are in constant motion. The movement of bodies in space is observed at all scale levels, starting with the movement of elementary particles in the atoms of matter and ending with the accelerated movement of galaxies in the Universe. In any case, the process of movement occurs with acceleration. In this article, we will consider in detail the concept of tangential acceleration and give a formula by which it can be calculated.

Kinematic quantities

Before talking about tangential acceleration, let's consider what quantities it is customary to characterize the arbitrary mechanical movement of bodies in space.

First of all, this is the path L. It shows the distance in meters, centimeters, kilometers, and so on, the body has traveled for a certain period of time.

The second important characteristic in kinematics is the speed of the body. Unlike the path, it is a vector quantity and is directed along the trajectorybody movements. Velocity determines the rate of change of spatial coordinates in time. The formula for calculating it is:

v¯=dL/dt

Speed is the time derivative of the path.

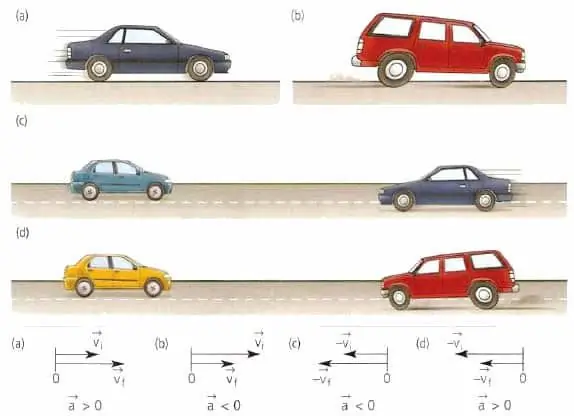
Finally, the third important characteristic of the movement of bodies is acceleration. According to the definition in physics, acceleration is a quantity that determines the change in speed with time. The formula for it can be written as:

a¯=dv¯/dt

Acceleration, like speed, is also a vector quantity, but unlike it, it is directed in the direction of speed change. The direction of acceleration also coincides with the vector of the resulting force acting on the body.

Trajectory and acceleration

Many problems in physics are considered within the framework of rectilinear motion. In this case, as a rule, they do not talk about the tangential acceleration of the point, but work with linear acceleration. However, if the movement of the body is not linear, then its full acceleration can be decomposed into two components:

tangent;
normal.

In the case of linear motion, the normal component is zero, so we don't talk about the vector expansion of acceleration.

Thus, the trajectory of motion largely determines the nature and components of the full acceleration. The trajectory of motion is understood as an imaginary line in space along which the body moves. Anya curvilinear trajectory leads to the appearance of non-zero acceleration components noted above.

Determination of tangential acceleration

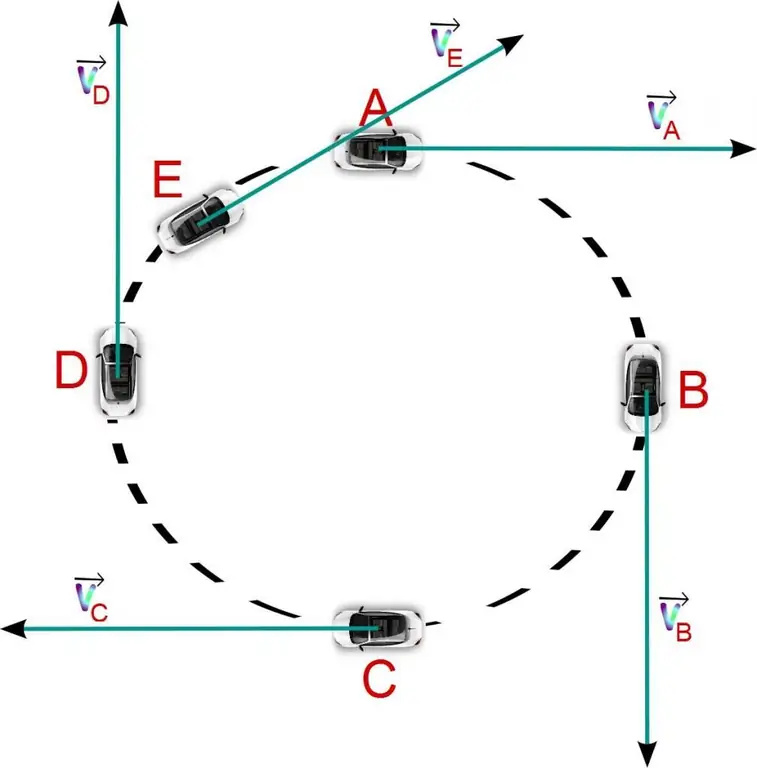
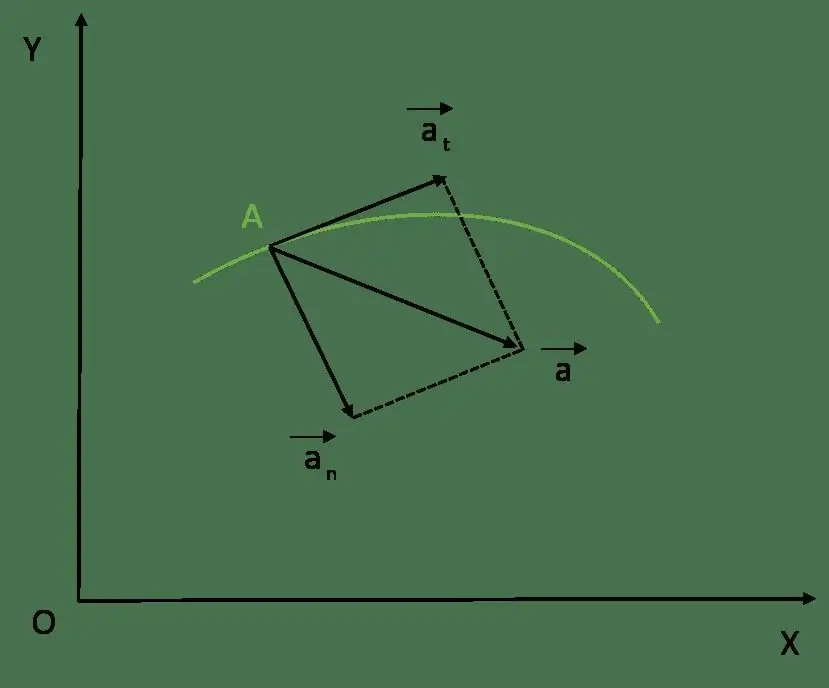
Tangential or, as it is also called, tangential acceleration is a component of full acceleration, which is directed tangentially to the trajectory of motion. Since the velocity is also directed along the trajectory, the tangential acceleration vector coincides with the velocity vector.

The concept of acceleration as a measure of change in speed was given above. Since speed is a vector, it can be changed either modulo or directionally. The tangential acceleration determines only the change in the speed modulus.

Note that in the case of rectilinear motion, the velocity vector does not change its direction, therefore, in accordance with the above definition, tangential acceleration and linear acceleration are the same value.

Getting the tangential acceleration equation

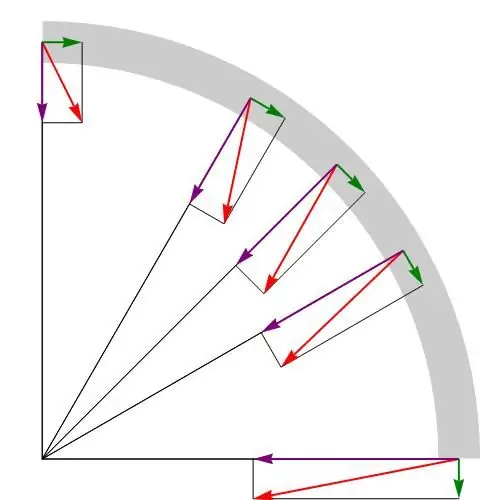
Assume that the body moves along some curved trajectory. Then its speed v¯ at the chosen point can be represented as follows:

v¯=vu_t¯

Here v is the modulus of the vector v¯, u_{t¯ is the unit velocity vector directed tangentially to the trajectory.}

Using the mathematical definition of acceleration, we get:

a¯=dv¯/dt=d(vu_t¯)/dt=dv/dtu_t ¯ + vd(u_t¯)/dt

When finding the derivative, the property of the product of two functions was used here. We see that the total acceleration a¯ at the considered point corresponds to the sum of two terms. They are the tangent and normal acceleration of the point, respectively.

Let's say a few words about normal acceleration. It is responsible for changing the velocity vector, that is, for changing the direction of motion of the body along the curve. If we explicitly calculate the value of the second term, we get the formula for normal acceleration:

a=vd(u_t¯)/dt=v^{2/ r}

Normal acceleration is directed along the normal restored to the given point of the curve. In the case of circular motion, normal acceleration is centripetal.

Tangential acceleration equation a_{t¯ is:}

a_t¯=dv/dtu_t¯

This expression says that tangential acceleration corresponds not to a change in direction, but to a change in the velocity modulus v¯ over a moment of time. Since the tangential acceleration is directed tangentially to the considered point of the trajectory, it is always perpendicular to the normal component.

Tangential acceleration and total acceleration modulus

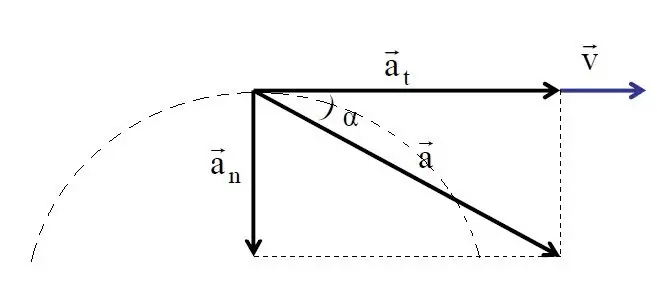
All the information above was presented that allows you to calculate the total acceleration through the tangent and normal. Indeed, since both components are mutually perpendicular, their vectors form the legs of a right triangle,whose hypotenuse is the total acceleration vector. This fact allows us to write the formula for the total acceleration module in the following form:

a=√(a² + a_t²⁾

The angle θ between full acceleration and tangential acceleration can be defined as follows:

θ=arccos(a_t/a)

The greater the tangential acceleration, the closer the directions of the tangent and full acceleration are.

Relationship between tangential and angular acceleration

A typical curvilinear trajectory along which bodies move in technology and nature is a circle. Indeed, the movement of gears, blades and planets around their own axis or around their luminaries occurs precisely in a circle. The movement corresponding to this trajectory is called rotation.

The kinematics of rotation is characterized by the same values as the kinematics of motion along a straight line, however, they have an angular character. So, to describe the rotation, the central angle of rotation θ, the angular velocity ω and the acceleration α are used. The following formulas are valid for these quantities:

ω=dθ/dt;

α=dω/dt

Assume that the body has made one revolution around the axis of rotation in time t, then for the angular velocity we can write:

ω=2pi/t

Linear speed in this case will be equal to:

v=2pir/t

Where r is the radius of the trajectory. The last two expressions allow us to writethe formula for the connection of two speeds:

v=ωr

Now we calculate the time derivative of the left and right sides of the equation, we get:

dv/dt=rdω/dt

The right side of the equality is the product of angular acceleration and the radius of the circle. The left side of the equation is the change in the velocity modulus, that is, the tangential acceleration.

Thus, tangential acceleration and a similar angular value are related by equality:

a_t=αr

If we assume that the disk is rotating, then the tangential acceleration of a point at a constant value of α will increase linearly with increasing distance from this point to the rotation axis r.

Next, we will solve two problems using the above formulas.

Determination of tangential acceleration from a known velocity function

It is known that the speed of a body that moves along a certain curved trajectory is described by the following function of time:

v=2t2+ 3t + 5

It is necessary to determine the formula for the tangential acceleration and find its value at time t=5 seconds.

First, let's write the formula for the tangential acceleration module:

a_t=dv/dt

That is, to calculate the function a_{t(t), you should determine the derivative of the speed with respect to time. We have:}

a_t=d(2t^{2+ 3t + 5)/dt=4t + 3}

Substituting time t=5 seconds into the resulting expression, we arrive at the answer: a_t=23 m/s^2.

Note that the graph of velocity versus time in this problem is a parabola, while the graph of tangential acceleration is a straight line.

Tangential acceleration task

It is known that the material point began uniformly accelerated rotation from the zero moment of time. 10 seconds after the start of rotation, its centripetal acceleration became equal to 20 m/s2. It is necessary to determine the tangential acceleration of a point after 10 seconds, if it is known that the radius of rotation is 1 meter.

First, write down the formula for centripetal or normal acceleration a_c: