Everyone who is familiar with technology and physics knows about the concept of acceleration. Nevertheless, few people know that this physical quantity has two components: tangential acceleration and normal acceleration. Let's take a closer look at each of them in the article.
What is acceleration?

In physics, acceleration is a quantity that describes the rate of change of speed. Moreover, this change is understood not only as the absolute value of the speed, but also as its direction. Mathematically, this definition is written as follows:
a¯=dv¯/dt.
Note that we are talking about the derivative of the change in the velocity vector, and not just its modulus.
Unlike speed, acceleration can take both positive and negative values. If the speed is always directed along the tangent to the trajectory of movement of bodies, then the acceleration is directed towards the force acting on the body, which follows from Newton's second law:
F¯=ma¯.
Acceleration is measured in meters per square second. So, 1 m/s2 means that the speed increases by 1 m/s for every second of movement.
Straight and curved motion paths and acceleration
Objects around us can move either in a straight line or along a curved path, for example, in a circle.
In the case of movement in a straight line, the speed of the body changes only its modulus, but retains its direction. This means that the total acceleration can be calculated like this:
a=dv/dt.
Note that we have omitted the vector icons above speed and acceleration. Since the full acceleration is directed tangentially to the rectilinear trajectory, it is called tangential or tangential. This acceleration component describes only the change in the absolute value of the speed.
Now suppose that the body moves along a curved path. In this case, its speed can be represented as:
v¯=vu¯.
Where u¯ is the unit velocity vector directed along the tangent to the trajectory curve. Then the total acceleration can be written in this form:
a¯=dv¯/dt=d(vu¯)/dt=dv/dtu¯ + vdu¯/dt.
This is the original formula for normal, tangential and total acceleration. As you can see, the equality on the right side consists of two terms. The second of them is different from zero only for curvilinear movement.
Tangential acceleration and normal acceleration formulas

The formula for the tangential component of the total acceleration has already been given above, let's write it again:
at¯=dv/dtu¯.
The formula shows that the tangential acceleration does not depend on where the velocity vector is directed, and whether it changes in time. It is determined solely by the change in the absolute value v.
Now write down the second component - normal acceleration a¯:
a¯=vdu¯/dt.
It is easy to show geometrically that this formula can be simplified to this form:
a¯=v2/rre¯.
Here r is the curvature of the trajectory (in the case of a circle it is its radius), re¯ is an elementary vector directed towards the center of curvature. We have obtained an interesting result: the normal component of acceleration differs from the tangential one in that it is completely independent of the change in the velocity module. So, in the absence of this change, there will be no tangential acceleration, and the normal one will take on a certain value.
Normal acceleration is directed towards the center of curvature of the trajectory, so it is called centripetal. The reason for its occurrence is the central forces in the system that change the trajectory. For example, this is the force of gravity when the planets rotate around the stars, or the tension of the rope when the stone attached to it rotates.
Full Circular Acceleration
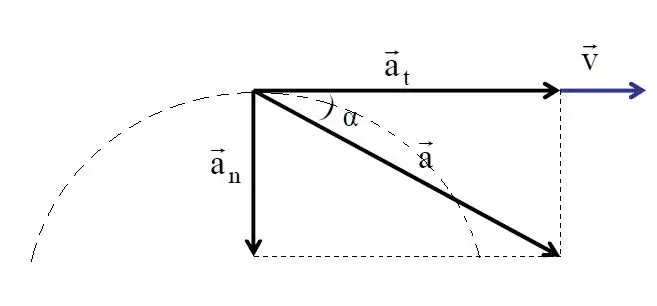
Having de alt with the concepts and formulas of tangential acceleration and normal acceleration, we can now proceed to the calculation of the total acceleration. Let's solve this problem using the example of rotating a body in a circle around some axis.
The considered two acceleration components are directed at an angle of 90o to each other (tangentially and to the center of curvature). This fact, as well as the property of the sum of vectors, can be used to calculate the total acceleration. We get:
a=√(at2+ a2).
From the formula for full, normal and tangential accelerations (accelerations a and at) two important conclusions follow:
- In the case of rectilinear movement of bodies, the full acceleration coincides with the tangential one.
- For uniform circular rotation, the total acceleration has only a normal component.

While moving in a circle, the centripetal force that gives the body acceleration akeeps it in a circular orbit, thereby preventing the fictitious centrifugal force.






