In our time, physics has become a very common science. It is literally present everywhere. The most elementary example: an apple tree grows in your yard, and fruits ripen on it, the time comes and the apples begin to fall, but in what direction do they fall? Thanks to the law of universal gravitation, our fetus falls to the ground, that is, it goes down, but not up. It was one of the most famous examples of physics, but let's pay attention to thermodynamics, or more precisely, to phase equilibria, which are no less important in our life.
Thermodynamics

First of all, let's look at this term. ΘερΜοδυναΜική - this is how the word looks in Greek. The first part ΘερΜo means "warmth", and the second δυναΜική means "strength". Thermodynamics is a branch of physics that studies the properties of a macroscopic system, as well as various ways of converting and transferring energy. In this section, various states and processes are specially studied so that the concept of temperature can be introduced into the description (this is a physical quantity that characterizes a thermodynamic system and is measured usingcertain appliances). All ongoing processes in thermodynamic systems are described only by microscopic quantities (pressure and temperature, as well as the concentration of components).
Clapeyron-Clausius equation
Every physicist knows this equation, but let's break it down piece by piece. It refers to the equilibrium processes of the transition of certain matter from one phase to another. This is clearly seen in such examples: melting, evaporation, sublimation (one of the ways to preserve products, which takes place by completely removing moisture). The formula clearly shows the ongoing processes:
- n=PV/RT;
- where T is the temperature of the substance;
- P-pressure;
- R-specific heat of phase transition;
- V-change in specific volume.
The history of the creation of the equation

The Clausius-Clapeyron equation is an excellent mathematical explanation of the second law of thermodynamics. Also referred to as the "Clausius inequality". Naturally, the theorem was developed by the scientist himself, who wanted to explain the relationship between the heat flow in the system and entropy, as well as its environment. This equation was developed by Clausius in his attempts to explain and quantify entropy. In the literal sense, the theorem gives us the opportunity to determine whether a cyclic process is reversible or irreversible. This inequality offers us a quantitative formula for understanding the second law.
The scientist was one of the first to work on the idea of entropy, and even gave itprocess name. What is now known as Clausius's theorem was first published in 1862 in Rudolf's sixth work, On the Use of the Transformation Equivalence Theorem for Interior Work. The scientist tried to show a proportional relationship between entropy and energy flow by heating (δ Q) in the system. In construction, this thermal energy can be converted into work, and it can be transformed into heat through a cyclic process. Rudolph proved that "the algebraic sum of all transformations occurring in a cyclic process can only be less than zero or, in extreme cases, equal to zero."
Closed isolated system

Isolated system is one of the following:
- Physical system is far from others that do not interact with them.
- The thermodynamic system is closed by rigid immovable walls through which neither matter nor energy can pass.
Despite the fact that the subject is internally related to its own gravity, an isolated system is usually taken beyond the limits of external gravitational and other distant forces.
This can be contrasted with what (in the more general terminology used in thermodynamics) is called a closed system surrounded by selective walls through which energy can be transferred in the form of heat or work, but not matter. And with an open system in which matter and energy enters or exits, although it may have various impenetrable walls inparts of its borders.
An isolated system obeys the conservation law. Most often in thermodynamics, matter and energy are considered as separate concepts.
Thermodynamic transitions
To understand quantum phase transitions, it is useful to compare them with classical transformations (also called thermal inversions). CPT describes the cusp in the thermodynamic properties of the system. It signals the reorganization of particles. A typical example is the freezing transition of water, which describes a smooth transition between a liquid and a solid. Classical phase growths are due to the competition between the energy of the system and the entropy of its thermal fluctuations.
A classical system has no entropy at zero temperature and therefore no phase transformation can occur. Their order is determined by the first discontinuous derivative thermodynamic potential. And, of course, it has the first order. Phase transformations from a ferromagnet to a paramagnet are continuous and second order. These constant changes from an ordered to a disordered phase are described by an order parameter that is zero. For the above ferromagnetic transformation, the order parameter will be the total magnetization of the system.
Gibbs potential
The Gibbs Free Energy is the maximum amount of work without expansion that can be removed from a thermodynamic closed system (that can exchange heat and work with the environment). Suchthe maximum result can be obtained only in a completely reversible process. When the system transforms back from the first state to the second, the reduction in the Gibbs free energy is equal to that performed by the system in its environment, minus the work of the pressure forces.
States of balance

Thermodynamic and mechanical equilibrium is an axiomatic concept of thermodynamics. This is the internal state of one or more systems that are connected by more or less permeable or impermeable walls. In this state, there are no pure macroscopic flows of matter or energy, either within a system or between systems.
In its own conception of the state of internal equilibrium, macroscopic change does not occur. Systems are simultaneously in mutual thermal, mechanical, chemical (constant), radiation equilibria. They may be in the same form. In this process, all views are saved at once and indefinitely until the physical operation is broken. In macroscopic equilibrium, perfectly precise balanced exchanges take place. The above proof is a physical explanation of this concept.
Basics
Each laws, theorems, formulas have their own foundations. Let's look at the 3 foundations of the law of phase equilibrium.
- Phase is a form of matter, homogeneous in chemical composition, physical state and mechanical balance. Typical phases are solid, liquid and gaseous. Two immiscible liquids (or liquid mixtures with different compositions) separated by a separate boundary are considered two different phases and immiscible solids.
- The number of components (C) is the number of chemically independent components of the system. The minimum number of independent species required to determine the composition of all phases of the system.
- The number of degrees of freedom (F) in this context is the number of intensive variables that are independent of each other.
Classification by phase equilibria
- Reactions of continuous net transfer (often called solid state reactions) occur between solid matter of different composition. They may include elements found in liquids (H, C), but these elements are retained in solid phases, so no liquid phases are involved as reactants or products (H2O, CO 2). Solid pure transfer reactions can be continuous or discontinuous, or terminal.
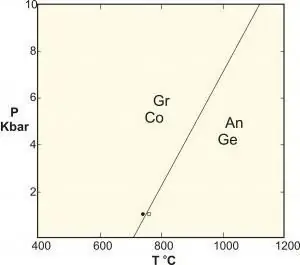
- Polymorphic are a special type of solid-state reaction that includes phases of identical composition. Classical examples are the reactions between aluminum silicates kyanite-sillimanite-andalusite, the conversion of graphite to diamond at high pressure, and the equilibrium of calcium carbonate.
Laws of equilibrium

The Gibbs Factory Rule was proposed by Josiah Willard Gibbs in his famous paper titled "The Equilibrium of Heterogeneous Substances", published from 1875 to 1878. It applies tonon-reactive multicomponent heterogeneous systems in thermodynamic equilibrium and is a given equality:
- F=C-P+2;
- where F is the number of degrees of freedom;
- C - number of components;
- P - number of phases in thermodynamic equilibrium with each other.
The number of degrees of freedom is the number of unoccupied intensive variables. The largest number of thermodynamic parameters, such as temperature or pressure, that can vary simultaneously and arbitrarily without affecting each other. An example of a one-component system is one with a single pure chemical, while two-component systems, such as mixtures of water and ethanol, have two independent components. Typical phase transitions (phase equilibrium) are solids, liquids, gases.
Phase rule at constant pressure
For applications in materials science dealing with phase changes between different solid structures, a constant pressure often occurs (e.g. one atmosphere) and is ignored as a degree of freedom, so the rule becomes: F=C - P + 1.
This formula is sometimes introduced under the name "condensed phase rule", but as we know, it is not applicable to these systems that are subject to high pressures (for example, in geology), since the consequences of these pressures can cause catastrophic consequences.
It may seem that phase equilibrium is just an empty phrase, and there are few physical processes in which this momentis involved, but, as we have seen, without it, many of the laws we know do not work, so you need to get a little familiar with these unique, colorful, albeit a little bit boring rules. This knowledge has helped many people. They learned how to apply them to themselves, for example, electricians, knowing the rules for working with phases, can protect themselves from unnecessary danger.






