One of the most difficult and incomprehensible topics of university mathematics is integration and differential calculus. You need to know and understand these concepts, as well as be able to apply them. Many university technical disciplines are tied to differentials and integrals.
Brief information about equations
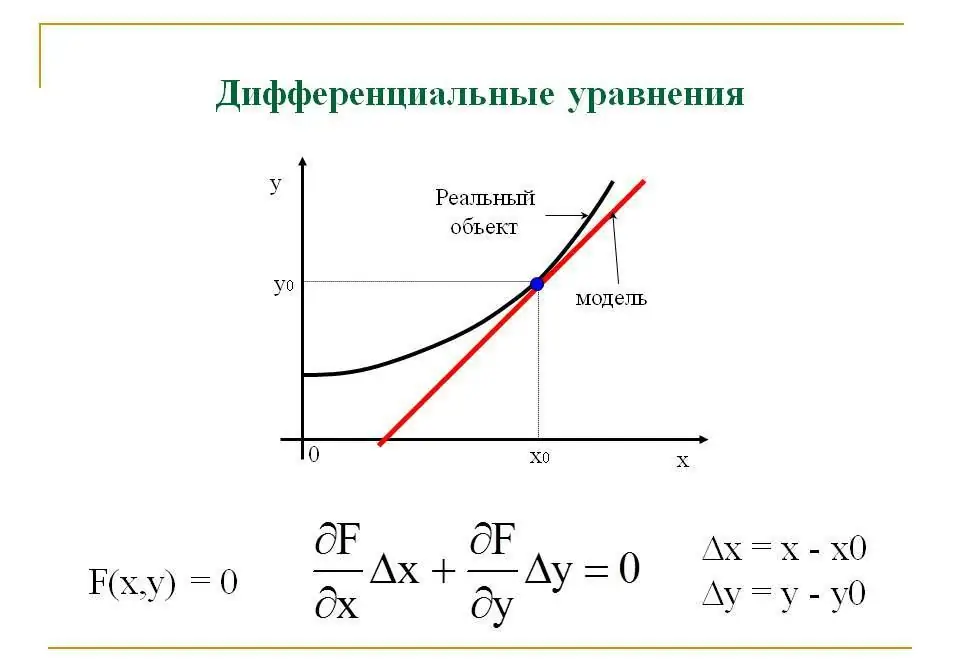
These equations are one of the most important mathematical concepts in the educational system. A differential equation is an equation that relates the independent variables, the function to be found, and the derivatives of that function to the variables that are assumed to be independent. Differential calculus for finding a function of one variable is called ordinary. If the desired function depends on several variables, then one speaks of a partial differential equation.
In fact, finding a certain answer to the equation comes down to integration, and the solution method is determined by the type of equation.
First order equations

A first-order differential equation is an equation that can describe a variable, a desired function, and its first derivative. Such equations can be given in three forms: explicit, implicit, differential.
Concepts needed to solve
Initial condition - setting the value of the desired function for a given value of a variable that is independent.
Solution of a differential equation - any differentiable function, exactly substituted into the original equation, turns it into identically equal. The solution obtained, which is not explicit, is the integral of the equation.
The general solution of differential equations is a function y=y(x;C), which can satisfy the following judgments:
- A function can have only one arbitrary constant С.
- The resulting function must be a solution to the equation for any arbitrary values of an arbitrary constant.
- With a given initial condition, an arbitrary constant can be defined in a unique way so that the resulting particular solution will be consistent with the given early initial condition.
In practice, the Cauchy problem is often used - finding a solution that is particular and can be compared with the condition set at the beginning.
Cauchy's theorem is a theorem that emphasizes the existence and uniqueness of a particular solution in differential calculus.
Geometric sense:
- General solution y=y(x;C)equation is the total number of integral curves.
- Differential calculus allows you to connect the coordinates of a point in the XOY plane and the tangent drawn to the integral curve.
- Setting the initial condition means setting a point on the plane.
- To solve the Cauchy problem means that from the whole set of integral curves representing the same solution of the equation, it is necessary to select the only one passing through the only possible point.
- Fulfillment of the conditions of Cauchy's theorem at a point means that an integral curve (moreover, only one) necessarily passes through the chosen point in the plane.
Separable variable equation
By definition, a differential equation is an equation where its right side describes or is reflected as a product (sometimes a ratio) of two functions, one depending only on "x", and the other - only on "y". A clear example for this kind: y'=f1(x)f2(y).
To solve equations of a particular form, you must first transform the derivative y'=dy/dx. Then, by manipulating the equation, you need to bring it to a form where you can integrate the two parts of the equation. After the necessary transformations, we integrate both parts and simplify the result.

Homogeneous equations
By definition, a differential equation can be called homogeneous if it has the following form: y'=g(y/x).
In this case, the replacement y/x=is most often usedt(x).
To solve such equations, it is necessary to reduce a homogeneous equation to a form with separable variables. To do this, you must perform the following operations:
- Display, expressing the derivative of the original function, from any original function as a new equation.
- The next step is to transform the resulting function into the form f(x;y)=g(y/x). In simpler words, make the equation contain only the ratio y/x and constants.
- Make the following replacement: y/x=t(x); y=t(x)x; y'=t'x + t. The substitution made will help divide the variables in the equation, gradually bringing it to a simpler form.
Linear equations
The definition of such equations is as follows: a linear differential equation is an equation where its right side is expressed as a linear expression with respect to the original function. The desired function in this case: y'=a(x)y + b(x).
Let's rephrase the definition as follows: any equation of the 1st order will become linear in its form if the original function and its derivative are included in the first degree equation and are not multiplied by each other. The "classical form" of a linear differential equation has the following structure: y' + P(x)y=Q(x).
Before solving such an equation, it should be converted to the "classical form". The next step will be the choice of the solution method: the Bernoulli method or the Lagrange method.
Solving the equation withusing the method introduced by Bernoulli, implies the substitution and reduction of a linear differential equation to two equations with separate variables relative to the functions U(x) and V(x), which were given in their original form.
The Lagrange method is to find a general solution to the original equation.
- It is necessary to find the same solution of the homogeneous equation. After searching, we have the function y=y(x, C), where C is an arbitrary constant.
- We are looking for a solution to the original equation in the same form, but we consider C=C(x). We substitute the function y=y(x, C(x)) into the original equation, find the function C(x) and write down the solution of the general original equation.
Bernoulli equation
Bernoulli's equation - if the right side of the calculus takes the form f(x;y)=a(x)y + b(x)yk, where k is any possible rational numerical value, not taking as an example cases when k=0 and k=1.
If k=1, then the calculus becomes separable, and when k=0, the equation remains linear.
Let's consider the general case of solving this type of equation. We have the standard Bernoulli equation. It must be reduced to a linear one, for this you need to divide the equation by yk. After this operation, replace z(x)=y1-k. After a series of transformations, the equation will be reduced to a linear one, most often by the substitution method z=UV.
Equations in total differentials
Definition. An equation with the structure P(x;y)dx + Q(x;y)dy=0 is called an equation in fulldifferentials, if the following condition is met (in this condition "d" is a partial differential): dP(x;y)/dy=dQ(x;y)/dx.
All first-order differential equations considered earlier can be displayed as differentials.

Such calculations are solved in several ways. But, however, they all begin with a condition check. If the condition is satisfied, then the leftmost region of the equation is the total differential of the yet unknown function U(x;y). Then, in accordance with the equation, dU (x; y) will be equal to zero, and therefore the same integral of the equation in total differentials will be displayed in the form U (x; y) u003d C. Therefore, the solution of the equation is reduced to finding the function U (x; y).
Integrating factor
If the condition dP(x;y)/dy=dQ(x;y)/dx is not met in the equation, then the equation does not have the form that we considered above. But sometimes it is possible to choose some function M(x; y), when multiplied by which the equation takes the form of an equation in full "diffurs". The function M (x;y) is referred to as the integrating factor.
An integrator can only be found when it becomes a function of only one variable.






