There are all kinds of mechanical devices. Some of them are familiar to us from childhood. These are, for example, watches, bicycles, spinning tops. We learn about others as we get older. These are motors of cars, winches of cranes and others. Every moving mechanism uses some kind of system to make the wheels turn and the machine work. One of the most interesting and popular is the planetary mechanism. Its essence lies in the fact that the machine is driven by wheels or gears that interact with each other in a special way. Let's take a closer look at it.
General information
The planetary gear and the planetary mechanism are so named by analogy with our solar system, which can be conditionally represented as follows: in the center there is a "sun" (the central wheel in the mechanism). "Planets" (small wheels or satellites) move around it. All these parts in the planetary gear have external teeth. The conditional solar system has a boundary in its diameter. Roleit is performed in the planetary mechanism by a large wheel or epicycle. It also has teeth, only internal ones. Most of the work in this design is performed by the carrier, which is a lever mechanism. Movement can be carried out in different ways: either the sun will rotate, or the epicycle, but always together with the satellites.
During the operation of the planetary mechanism, another design can be used, for example, two suns, satellites and a carrier, but without an epicycle. Another option is two epicycles, but without the sun. Carrier and satellites must always be present. Depending on the number of wheels and the location of their axes of rotation in space, the design can be simple or complex, flat or spatial.
To fully understand how such a system works, you need to understand the details.
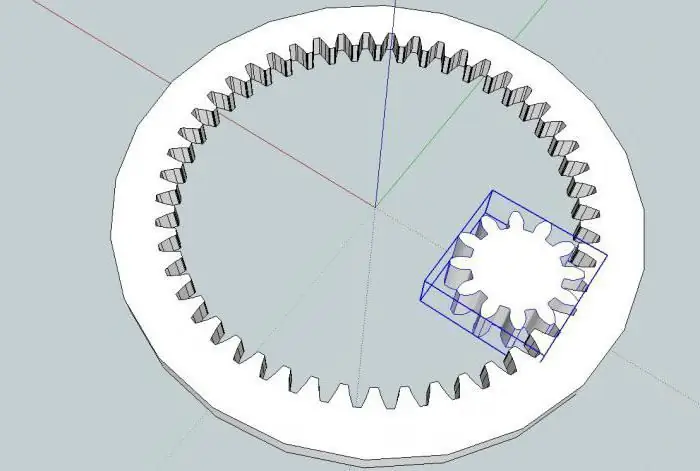
Location of elements
The simplest form of planetary gear includes three sets of gears with varying degrees of freedom. The above satellites rotate around their axes and at the same time around the sun, which remains in place. The epicycle connects the planetary mechanism from the outside and also rotates by means of an alternate engagement of the teeth (it and the satellites). This design is capable of changing the torque (angular velocities) in one plane.
In a simple planetary mechanism, the sun and satellites can rotate, while the epicenter remains fixed. In any case, the angular velocities of all components are not chaotic, but have a linear dependence on each other. As the media rotates, it provideslow speed high torque output.
That is, the essence of the planetary gear is that such a design is able to change, expand and add torque and angular velocity. Rotational movements in this case occur in one geometric axis. The necessary transmission element of various vehicles and mechanisms is installed.

Features of structural materials and schemes
However, a fixed component is not always necessary. In differential systems, each element rotates. Planetary gears like this one have one output driven (controlling) two inputs. For example, a differential that controls an axle in a car is a similar gear.
Such systems work on the same principle as parallel shaft structures. Even a simple planetary gear has two inputs, the fixed ring gear is a constant input of zero angular velocity.
Detailed description of devices
Mixed planetary structures can have a different number of wheels, as well as different gears through which they are connected. The presence of such details greatly expands the possibilities of the mechanism. Composite planetary structures can be assembled so that the shaft of the carrier platform moves at high speed. As a result, some problems with reduction gear, sun gear and others can be eliminated in the process of improving the device.
Thus, as seen fromgiven information, the planetary mechanism works on the principle of transferring rotation between links that are central and mobile. At the same time, complex systems are more in demand than simple ones.
Configuration Options
It is possible to use wheels (gears) of various configurations in the planetary mechanism. Suitable standard with straight teeth, helical, worm, chevron. The type of engagement will not affect the general principle of operation of the planetary mechanism. The main thing is that the axes of rotation of the carrier and the central wheels coincide. But the axes of the satellites can be located in other planes (crossing, parallel, intersecting). An example of crossed is an interwheel differential, in which the gears are conical. An example of crossed is a self-locking differential with a worm gear (Torsen).
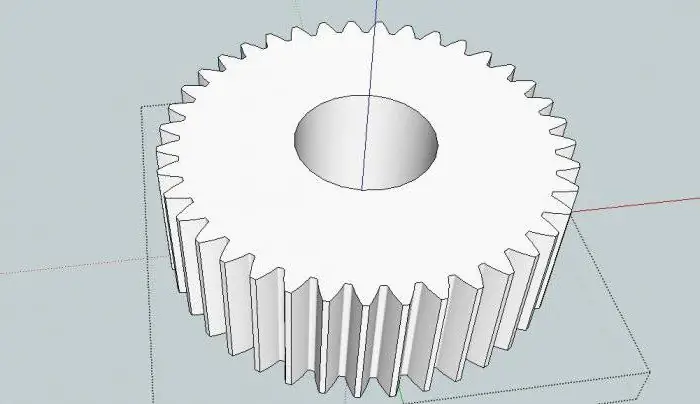
Simple and complex devices
As noted above, the scheme of the planetary mechanism always includes a carrier and two central wheels. There can be any number of satellites. This is the so-called simple or elementary device. In such mechanisms, designs can be as follows: "SVS", "SVE", "EVE", where:
- S is the sun.
- B - carrier.
- E is the epicenter.
Each such set of wheels + satellites is called a planetary gear set. In this case, all wheels must rotate in the same plane. Simple mechanisms are single- and double-row. They are rarely used in various technical devices and machines. An examplecan serve as a planetary bicycle mechanism. According to this principle, the sleeve works, thanks to which the movement is carried out. Its design was created according to the "SVE" scheme. Satellites in not 4 pieces. In this case, the sun is rigidly attached to the axis of the rear wheel, and the epicenter is movable. It is forced to rotate by a cyclist pressing the pedals. In this case, the transmission speed, and therefore the rotation speed, may change.
More often you can find complex gear planetary mechanisms. Their schemes can be very different, which depends on what this or that design is intended for. As a rule, complex mechanisms consist of several simple ones, created according to the general rule for a planetary gear. Such complex systems are two-, three- or four-row. Theoretically, it is possible to create structures with a large number of rows, but in practice this does not occur.
Planar and spatial devices
Some people think that a simple planetary gear must be flat. This is only partly true. Complex devices can also be flat. This means that the planetary gears, no matter how many of them are used in the device, are in one or in parallel planes. Spatial mechanisms have planetary gears in two or more planes. In this case, the wheels themselves may be smaller than in the first version. Note that the flat planetary mechanism is the same as the spatial one. The difference is only in the area occupied by the device, that is, in compactness.
Degrees of freedom
This is the name of the collectioncoordinates of rotation, which allows to determine the position of the system in space at a given time. In fact, every planetary mechanism has at least two degrees of freedom. That is, the angular speeds of rotation of any link in such devices are not linearly related, as in other gears. This allows you to get at the output angular velocities that are not the same as those at the input. This can be explained by the fact that in the differential connection in the planetary mechanism there are three elements in any row, and the rest will be connected with it linearly, through any one element of the row. Theoretically, it is possible to create planetary systems with three or more degrees of freedom. But in practice, they are inoperable.

Planetary Gear Ratio
This is the most important characteristic of rotational motion. It allows you to determine how many times the moment of force on the driven shaft has increased in relation to the moment of the driving shaft. You can determine the gear ratio using the formulas:
i=d2/d1=Z2/Z1=M2/M1=W1/W2=n1/n2, where:
- 1 - leading link.
- 2 - slave link.
- d1, d2 - diameters of the first and second links.
- Z1, Z2 - number of teeth.
- M1, M2 are torques.
- W1 W2 - angular speeds.
- n1 n2 - speed.
Thus, when the gear ratio is higher than one on the driven shaft, the moment of force increases, and the frequency and angular velocity decrease. This should always be taken into account when creating a design, becausethe gear ratio in planetary mechanisms depends on how many teeth the wheels have, and which element of the row is the leading one.
Scope of application
In today's world there are many different machines. Many of them work with the help of planetary gears.
They are used in automobile differentials, planetary gears, in the kinematic schemes of complex machine tools, in aircraft air engine gearboxes, in bicycles, in combines and tractors, in tanks and other military equipment. According to the principles of planetary gear, many gearboxes work in the drives of electric generators. Consider another such system.
Planetary turning gear
This design is used in some tractors, tracked vehicles and tanks. A simple diagram of the device is shown in the figure below.
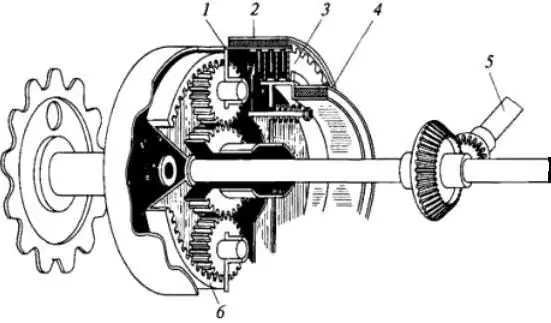
The principle of operation of the planetary rotation mechanism is as follows: the carrier (position 1) is connected to the brake drum (2) and the drive wheel located in the caterpillar. The epicycle (6) is connected to the transmission shaft (position 5). The sun (8) is connected to the clutch disc (3) and the swing brake drum (4). When the locking clutch is engaged and the band brakes are turned off, the satellites will not rotate. They will become like levers, as they are connected with the sun (8) and the epicycle (6) by means of teeth. Therefore, they force them and the carrier to simultaneously rotate around a common axis. In this case, the angular velocity is the same.
When disengaging the lockup clutch and applying the braketurning the sun will begin to stop, and the satellites will begin to move around their axes. Thus, they create a moment on the carrier and rotate the drive wheel of the caterpillar.
Wear
In terms of service life and damping, in linear planetary systems, the load distribution is noticeable among the main components.
Thermal and cyclic fatigue can increase in them due to the limited load distribution and the fact that planetary gears can rotate quite quickly on their axes. Moreover, at high speeds and gear ratios of the planetary gear, centrifugal forces can greatly increase the amount of movement. It should also be noted that as manufacturing accuracy decreases and the number of satellites increases, the tendency for imbalance increases.
These devices and their systems may even be subject to wear and tear. Some designs will be sensitive to even small imbalances and may require quality and expensive assembly components. The exact location of the planetary pins around the sun gear axis can be a key.
Other planetary arrangements that help balance loads include the use of floating subassemblies or "soft" mounts to keep the sun or epicenter moving as long as possible.

Fundamentals of synthesis of planetary devices
This knowledge is needed when designing and creating machine assemblies. The concept of "synthesis of planetary mechanisms" is to calculate the number of teethin the sun, epicenter and satellites. In this case, a number of conditions must be met:
- The gear ratio must be equal to the set value.
- Gear teeth engagement must be correct.
- It is necessary to ensure the alignment of the input shaft and the output shaft.
- Neighbourhood required (satellites must not interfere with each other).
Also, when designing, you need to take into account the dimensions of the future structure, its weight and efficiency.
If the gear ratio (n) is given, then the number of teeth on the sun (S) and on the planetary gears (P) must satisfy the equation:
n=S/P
If we assume that the number of teeth at the epicenter is early (A), then with the carrier locked, the equality should be observed:
n=-S/A
If the epicenter is fixed, then the following equality will be true:
n=1+ A/S
This is how the planetary mechanism is calculated.

Advantages and disadvantages
There are several types of transmission that are successfully used in various devices. Planetary among them stands out for the following advantages:
- Provides less load on each tooth of the wheels (both the sun, and the epicenter, and satellites) due to the fact that the load on them is distributed more evenly. This has a positive effect on the service life of the structure.
- With the same power, the planetary gear has smaller dimensions and weight than other types of transmission.
- Ability to achieve higher gear ratios withfewer wheels.
- Ensure less noise.
Disadvantages of planetary gears:
- Need more precision in their manufacture.
- Low efficiency with a relatively large gear ratio.






