To be able to solve various problems on the movement of bodies in physics, you need to know the definitions of physical quantities, as well as the formulas by which they are related. This article will address the questions of what is tangential velocity, what is full acceleration and what components make it up.
The concept of speed
The two main quantities of the kinematics of moving bodies in space are speed and acceleration. Speed describes the speed of movement, so the mathematical notation for it is as follows:
v¯=dl¯/dt.
Here l¯ - is the displacement vector. In other words, speed is the time derivative of the distance travelled.
As you know, every body moves along an imaginary line, which is called a trajectory. The velocity vector is always directed tangentially to this trajectory, no matter where the moving body is.
There are several names for the quantity v¯, if we consider it together with the trajectory. Yes, since it is directedis tangential, it is called tangential velocity. It can also be spoken of as a linear physical quantity as opposed to angular velocity.
The speed is calculated in meters per second in SI, but in practice kilometers per hour are often used.
The concept of acceleration
Unlike speed, which characterizes the speed of the body passing the trajectory, acceleration is a quantity that describes the speed of change of speed, which is mathematically written as follows:
a¯=dv¯/dt.
Like speed, acceleration is a vector characteristic. However, its direction is not related to the velocity vector. It is determined by the change in direction v¯. If during the motion the speed does not change its vector, then the acceleration a¯ will be directed along the same line as the speed. Such acceleration is called tangential. If the speed changes direction, while maintaining the absolute value, then the acceleration will be directed towards the center of curvature of the trajectory. It's called normal.
Measured acceleration in m/s2. For example, the well-known free fall acceleration is tangential when an object rises or falls vertically. Its value near the surface of our planet is 9.81 m/s2, that is, for every second of falling, the speed of the body increases by 9.81 m/s.

The reason for the appearance of acceleration is not speed, but force. If the force F exertsaction on a body of mass m, then it will inevitably create an acceleration a, which can be calculated as follows:
a=F/m.
This formula is a direct consequence of Newton's second law.
Full, normal and tangential accelerations
Velocity and acceleration as physical quantities were discussed in the previous paragraphs. We will now take a closer look at what components make up the total acceleration a¯.
Assume that the body is moving with speed v¯ along a curved path. Then the equality will be true:
v¯=vu¯.
Vector u¯ has unit length and is directed along the tangent line to the trajectory. Using this representation of the speed v¯, we get the equality for the full acceleration:
a¯=dv¯/dt=d(vu¯)/dt=dv/dtu¯ + vdu¯/dt.
The first term obtained in the right equality is called tangential acceleration. Velocity is related to it by the fact that it quantifies the change in the absolute value of v¯, regardless of its direction.
The second term is the normal acceleration. It quantitatively describes the change in the velocity vector, without taking into account the change in its modulus.
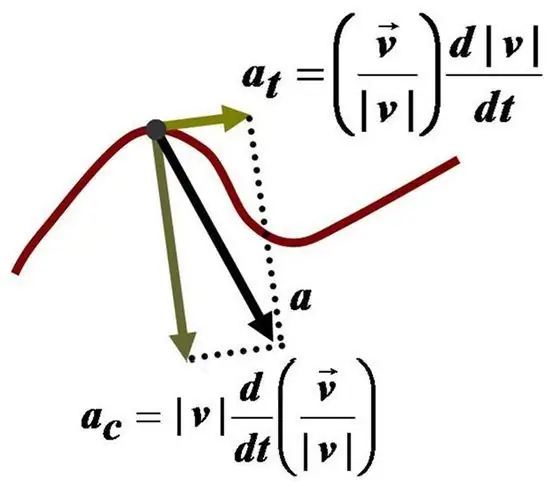
If we denote as atand a the tangential and normal components of the total acceleration a, then the modulus of the latter can be calculated by the formula:
a=√(at2+a2).
Relationship between tangential acceleration and speed
The corresponding connection is described by kinematic expressions. For example, in the case of movement in a straight line with constant acceleration, which is tangential (the normal component is zero), the expressions are valid:
v=att;
v=v0 ± att.
In the case of movement in a circle with constant acceleration, these formulas are also valid.
Thus, whatever the trajectory of the body, the tangential acceleration through the tangential velocity is calculated as the time derivative of its modulus, that is:
at=dv/dt.
For example, if the speed changes according to the law v=3t3+ 4t, then at will be equal to:
at=dv/dt=9t2+ 4.
Speed and normal acceleration

Let's write explicitly the formula for the normal component a, we have:
a¯=vdu¯/dt=vdu¯/dldl/dt=v2/r re¯
Where re¯ is a vector of unit length directed towards the center of curvature of the trajectory. This expression establishes the relationship between tangential velocity and normal acceleration. We see that the latter depends on the modulus v at a given time and on the radius of curvature r.
Normal acceleration occurs whenever the velocity vector changes, however it is zero ifthis vector keeps the direction. Talking about the value a¯ makes sense only when the curvature of the trajectory is a finite value.
We noted above that when moving in a straight line, there is no normal acceleration. However, in nature there is a type of trajectory, when moving along which a has a finite value, and at=0 for |v¯|=const. This path is a circle. For example, rotation with a constant frequency of a metal shaft, carousel or planet around its own axis occurs with constant normal acceleration a and zero tangential acceleration at.






