In the novel "The Secret of Two Oceans" and in the adventure film of the same name, the heroes did unimaginable things with ultrasonic weapons: they destroyed a rock, killed a huge whale, and destroyed the ship of their enemies. The work was published back in the 30s of the XX century, and then it was believed that in the near future the existence of a powerful ultrasonic weapon would become possible - it's all about the availability of technology. Today, science claims that ultrasonic waves as weapons are fantastic.

Another thing is the use of ultrasound for peaceful purposes (ultrasonic cleaning, drilling holes, crushing kidney stones, etc.). Next, we will understand how acoustic waves with large amplitude and sound intensity behave.
Powerful sounds feature
There is a concept of non-linear effects. These are effects peculiar only enoughstrong waves and depending on their amplitude. In physics, there is even a special section that studies powerful waves - nonlinear acoustics. A few examples of what she investigates are thunder, underwater explosions, seismic waves from earthquakes. Two questions arise.
- First: what is the power of sound?
- Second: what are non-linear effects, what is unusual about them, where are they used?
What is an acoustic wave
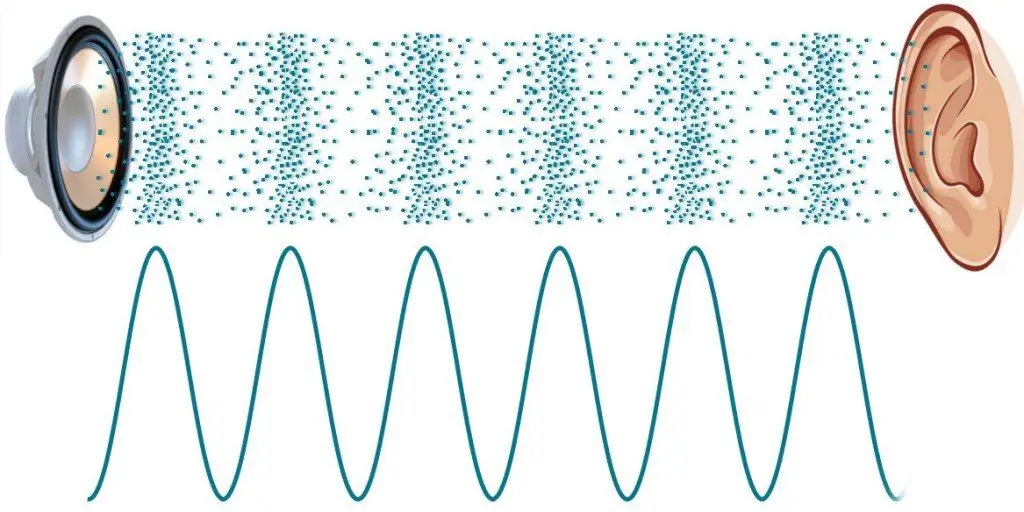
A sound wave is a section of compression-rarefaction that diverges in the medium. In any of its places, the pressure changes. This is due to a change in the compression ratio. Changes superimposed on the initial pressure that was in the environment are called sound pressure.
Sonic energy flow
A wave has energy that deforms the medium (if sound propagates in the atmosphere, then this is the energy of elastic deformation of air). In addition, the wave has the kinetic energy of the molecules. The direction of the flow of energy coincides with that in which the sound diverges. The flow of energy passing through a unit area per unit time characterizes the intensity. And this refers to the area perpendicular to the movement of the wave.
Intensity
Both intensity I and acoustic pressure p depend on the properties of the medium. We will not dwell on these dependencies, we will only give the sound intensity formula relating p, I and the characteristics of the medium - the density (ρ) and the speed of sound in the medium (c):
I=p02/2ρc.
Herep0 - acoustic pressure amplitude.

What is strong and weak noise? The force (N) is usually determined by the level of sound pressure - a value that is associated with the amplitude of the wave. The unit of sound intensity is the decibel (dB).
N=20×lg(p/pp), dB.
Here pp is the threshold pressure conditionally taken equal to 2×10-5 Pa. Pressure pp roughly corresponds to intensity Ip=10-12 W/m 2 is a very faint sound that can still be perceived by the human ear in air at a frequency of 1000 Hz. The sound is stronger the higher the acoustic pressure level.
Volume
Subjective ideas about the strength of sound are associated with the concept of loudness, that is, they are tied to the frequency range perceived by the ear (see table).

And what about when the frequency lies outside this range - in the field of ultrasound? It is in this situation (during experiments with ultrasound at frequencies of the order of 1 megahertz) that it is easier to observe nonlinear effects under laboratory conditions. We conclude that it makes sense to call powerful acoustic waves for which nonlinear effects become noticeable.
Nonlinear effects
It is known that an ordinary (linear) wave, the sound intensity of which is low, propagates in a medium without changing its shape. In this case, both rarefaction and compression regions move in space at the same speed - this is the speed of sound in the medium. If the sourcegenerates a wave, then its profile remains in the form of a sinusoid at any distance from it.
In an intense sound wave, the picture is different: areas of compression (sound pressure is positive) move at a speed exceeding the speed of sound, and areas of rarefaction - at a speed less than the speed of sound in a given medium. As a result, the profile changes a lot. The front surfaces become very steep, and the backs of the wave become more gentle. Such strong shape changes are the non-linear effect. The stronger the wave, the greater its amplitude, the faster the profile is distorted.
For a long time it was considered possible to transmit high energy densities over long distances using an acoustic beam. An inspiring example was a laser capable of destroying structures, punching holes, being at a great distance. It seems that the replacement of light with sound is possible. However, there are difficulties that make it impossible to create an ultrasonic weapon.
It turns out that for any distance there is a boundary value for the intensity of the sound that will reach the target. The greater the distance, the lower the intensity. And the usual attenuation of acoustic waves when passing through the medium has nothing to do with it. Attenuation increases markedly with increasing frequency. However, it can be chosen so that the usual (linear) attenuation at the required distances can be neglected. For a signal with a frequency of 1 MHz in water, this is 50 m, for ultrasound of a sufficiently large amplitude, it can be only 10 cm.
Let's imagine that a wave is generated in some place in space, the intensitythe sound of which is such that nonlinear effects will significantly affect its behavior. The oscillation amplitude will decrease with distance from the source. This will happen the sooner, the greater the initial amplitude p0. At very high values, the decay rate of the wave does not depend on the value of the initial signal p0. This process continues until the wave decays and the nonlinear effects stop. After that, it will diverge in a non-linear mode. Further attenuation occurs according to the laws of linear acoustics, i.e., it is much weaker and does not depend on the magnitude of the initial disturbance.
How then is ultrasound successfully used in many industries: they are drilled, cleaned, etc. With these manipulations, the distance from the emitter is small, so the nonlinear attenuation has not yet had time to gain momentum.

Why do shock waves have such a strong effect on obstacles? It is known that explosions can destroy structures located quite far away. But the shock wave is non-linear, so the decay rate must be higher than that of weaker waves.
The bottom line is this: a single signal does not act like a periodic one. Its peak value decreases with distance from the source. By increasing the amplitude of the wave (for example, the strength of the explosion), it is possible to achieve large pressures on the obstacle at a given (even if small) distance and thereby destroy it.






