The conductometric method of analysis is the measurement of electrolytic conductivity to monitor the progress of a chemical reaction. This science is widely applied in analytical chemistry, where titration is a standard method of operation. What is conductometry? In common practice in analytical chemistry, the term is used as a synonym for titration, while it is also used to describe non-titration applications. What is the benefit of using this analysis method? It is often used to determine the overall conductivity of a solution or to analyze the endpoint of a titration involving ions.
History
Conductive measurements began as early as the 18th century, when Andreas Baumgartner noticed that the s alt and mineral waters from Bad Gastein inAustria conduct electricity. Thus, the use of this method to determine the purity of water, which is often used today to test the effectiveness of water purification systems, began in 1776. Thus began the history of the conductometric method of analysis.
Friedrich Kohlrausch continued the development of this science in the 1860s, when he applied alternating current to water, acids and other solutions. Around this time, Willis Whitney, who was studying the interactions of sulfuric acid and chromium sulfate complexes, found the first conductometric endpoint. These findings culminated in potentiometric titration and the first instrument for volumetric analysis by Robert Behrend in 1883 in the titration of chloride and bromide HgNO3. Thus, the modern conductometric method of analysis is based on Behrend.
This development made it possible to test the solubility of s alts and the concentration of hydrogen ions, as well as acid-base and redox titrations. The conductometric method of analysis was improved with the development of the glass electrode, which began in 1909.
Titration
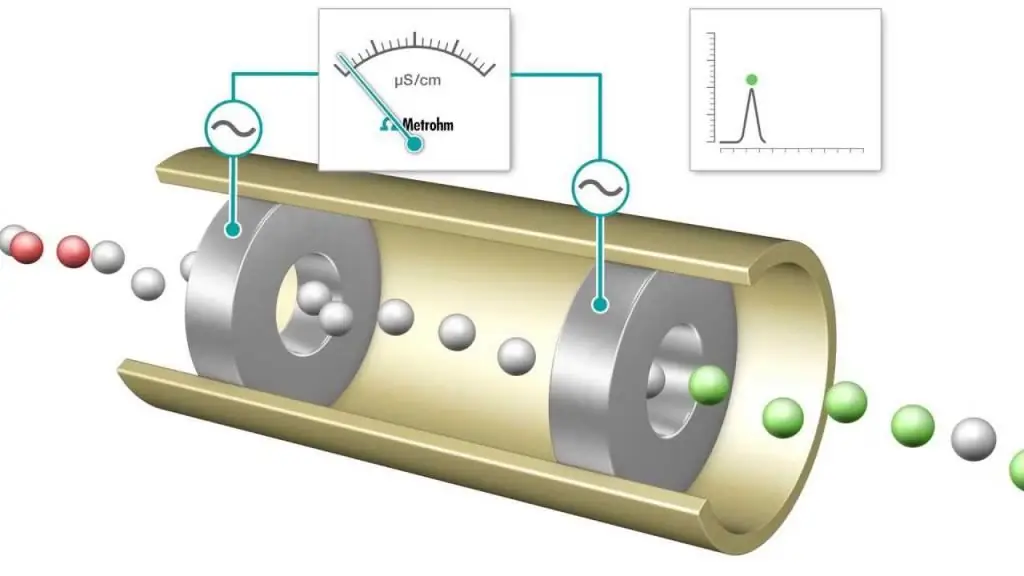
Conductometric titration is a measurement in which the electrolytic conductivity of a reaction mixture is continuously monitored by adding one reagent. The equivalence point is the point at which the conductivity suddenly changes. A noticeable increase or decrease in conductivity is associated with a change in the concentration of the two most highly conductive ions, hydrogen and hydroxide ions. This methodcan be used to titrate colored solutions or homogeneous suspension (e.g. wood pulp suspension) which cannot be used with conventional indicators.
Acid-base and redox titrations are often performed, which use common indicators to determine the end point, such as methyl orange, phenolphthalein for acid-base titration, and starch solutions for an iodometric-type redox process. However, electrical conductivity measurements can also be used as a tool to determine the endpoint, for example when observing a solution of HCl with the strong base NaOH.
Proton neutralization
As the titration progresses, the protons are neutralized to form NaOH by forming water. For each amount of NaOH added, an equivalent number of hydrogen ions are removed. In effect, the mobile H+ cation is replaced by the less mobile Na+ ion, and the conductivity of the titrated solution, as well as the measured cell conductivity, decrease. This continues until an equivalence point is reached at which a solution of sodium chloride NaCl can be obtained. If more base is added, there is an increase as more Na+ and OH- ions are added and the neutralization reaction no longer removes an appreciable amount of H+.

Consequently, when a strong acid is titrated with a strong base, the conductivity has a minimum at the equivalence point. This minimumcan be used instead of an indicator dye to determine the endpoint of a titration. The titration curve is a graph of measured values of conductivity or conductivity as a function of the volume of added NaOH solution. The titration curve can be used to graphically determine the equivalence point. The conductometric method of analysis (and its use) is extremely relevant in modern chemistry.
Reaction
For a reaction between a weak acid-weak base, the electrical conductivity first decreases somewhat, since few available H+ ions are used. Then the conductivity increases slightly up to the volume of the equivalence point due to the contribution of the s alt cation and the anion (this contribution in the case of a strong acid-strong base is negligible and is not considered there.) After reaching the equivalence point, the conductivity increases rapidly due to an excess of OH ions.
Conductivity detectors (conductometric method of analysis) are also used to measure electrolyte concentrations in aqueous solutions. The molar concentration of the analyte that creates the conductivity of the solution can be obtained from the measured electrical resistance of the solution.
Conductometric method of analysis: principle and formulas
(2.4.13) C=Constcell1Λm1Res, where Constcell is a constant value depending on the measuring cell, Res is the electrical resistance measured by the device (according to Ohm's law Res=I / V, and with a constant voltage V measurement I intensity allows you to calculate Res), and Λm is the equivalentconductivity for ionic particles. Although for practical purposes Λm can be considered constant, it depends on concentration according to Kohlrausch's law:
(2.4.14)=Хт Λm0-ΘC, where Θ is a constant, and Λm0 is the limiting molar conductivity characteristic of each ion. Molar conductivity, in turn, depends on temperature.
Scrit
The development of the conductometric method of measurement analysis has led scientists to new discoveries. The scientists determined the critical supersaturation ratio, Scrit, using conductometry in a homogeneous AgCl precipitation system in excess of Ag+ ions, using alkyl chloride hydrolysis as the source of CI ions.” They found Scrit=1.51, 1.73 and 1.85 at 15, 25 and 35°C respectively, where S=([Ag+][Cl-] / Ksp) 1/2 by their definition. If this definition of the supersaturation factor is converted to ours (S=[Ag+][Cl-] / Ksp), the results are 2.28, 2.99 and 3.42, respectively, in fairly good agreement with the results of the present study. However, the temperature dependence of Scrit is opposite to that described in the present study. Although the reason for this contradiction is not clear, the decrease in Scrit with increasing temperature may be quite reasonable, since the nucleation rate changes dramatically with a small change in ΔGm/ kT, and therefore ΔGm/ kT, which is proportional to T − 3 (lnSm) 2 according to the formula (1.4.12) is considered to be almost constant with temperature change in the given system. Incidentally, the definition of S must be [Ag +] [Cl -] / Ksp, since the supersaturation ratio in terms of[AgCl] monomer concentration is initially given as S=[AgCl] / [AgCl] (∞)=[Ag +] [Cl -] / Ksp.
Tanaka and Iwasaki
The history of the conductometric method of analysis was continued by two iconic Japanese scientists. Tanaka and Iwasaki studied the process of nucleation of AgCl and AgBr particles using the stopped flow method in combination with a multichannel spectrophotometer, which is useful for studying a fast process on the order of msec. They found that some specific silver halide complex AgXm (m-1), having a rather narrow UV absorption band, was formed instantly when a solution of AgC104 of the order of 10-4 mol dm-3 was mixed with a KX (X=Cl or Br) solution of the order of from 10-2 to 10-1 mol dm-3 followed by its rapid decay of about 10 ms with the formation of an intermediate product having a wide UV absorption and a much slower change in the spectrum of the intermediate product. They interpreted the intermediate as monodisperse cores (AgX) n consisting of n molecules and determined n from the apparent ratio -dC/dt α Cn at t=0 for various initial concentrations of C precursor AgXm (m-1) - (n=7 -10 for AgCl, n=3-4 for AgBr).

However, since the precursor AgXm (m − 1) decays in a non-stationary manner, the theory of quasi-stationary nucleation does not apply in this process, and thus the resulting value of n does not correspond to the nvalue of critical nuclei. If the intermediate product contains monodisperse nuclei n,formed at the expense of the monomeric complex, the ratio -dC / dt α C may not be preserved. Unless we assume that clusters smaller than n-mers are in equilibrium, ki − 1, ici − 1c1=ki, i − 1ci, with each other in a sequential reaction c1 → c2 → c3 →… → cn − 1 → cn., and only the last step cn − 1 → cn is irreversible; i.e. c1⇌c2⇌c3⇌… ⇌cn − 1 → cn.
Besides, it should be assumed that the concentrations of clusters from 2 to n-1 have negligible equilibrium concentrations. However, there seems to be no basis to justify these assumptions. On the other hand, we tried to calculate the radii of critical nuclei and the supersaturation coefficients S at the end of the fast process, using γ=101 mJ m − 2 for cubic AgCl19 and γ=109 mJ m − 2 for cubic AgBr20, assuming that the values of n, 7-10 for AgCl19 and 3-4 for AgBr20, are equivalent to the size of monodisperse nuclei, n. The conductometric method of analysis, reviews of which range from simply approving to admiring, gave a new birth to chemistry as a science.
As a result, scientists discovered the following formula: r=0.451 nm and S=105 for AgCl with n=9; r=0.358 nm and S=1230 for AgBr with n=4. Since their systems are comparable to those of Davis and Jones, which obtained a critical supersaturation of AgCl of about 1.7-2.0 at 25 °C. Using direct-mix conductometry in equal volumes of dilute aqueous solutions of AgNO3 and KCl, extremely high S values may not reflect actual supersaturation factors.in equilibrium with intermediate nuclei.
UV absorption
It seems more reasonable to attribute an intermediate with broad UV absorption to much larger than average nuclei with a wide size distribution generated by a non-stationary sequential reaction. The subsequent slow change of intermediate nuclei seems to be related to their maturation in Ostwald.

In the above context, the American chemist Nielsen also derived a similar naround 12 and a corresponding S greater than 103 for the nucleation of barium sulfate particles from turbidity measurements as a function of supersaturation, using n=dlogJ / dlogC in a Becher-Dering-like theory to the formula. (1.3.37), but giving (n+ 1) instead of n. Since solutions of barium ions and sulfate ions were directly mixed in this experiment, fast transient nucleation should have ended immediately after mixing, and what was measured could be the rate of slow subsequent Ostwald maturation and/or fusion of the generated nuclei. Apparently, this is the reason for the unreasonably small value of n and the extremely high supersaturation. Therefore, we must again note that some reservoir of monomeric species that releases them in response to their consumption is always necessary to achieve quasi-stationary nucleation in a closed system. All classical theories of nucleation, including the Becher-Döring theory, implicitly assume such a condition. Definition of conductometricanalysis method was given in the sections of the article above.
Other scientists have investigated the process of transient nucleation of silver halide by pulsed radiolysis of water containing methylene halide and silver ions, during which the methylene halide is decomposed to release halide ions by hydrated electrons generated by pulsed radiation in the range from 4 ns to 3 μs. The spectra of the products were recorded using a photomultiplier and streak camera and monomeric silver halide precursors were found to form over a time on the order of microseconds followed by a nucleation process similar to that observed by Tanaka and Iwasaki. Their results clearly show that the process of nucleation of silver halides by direct mixing of the reactants consists of two elementary steps; that is, the formation of a monomeric precursor of the order of μs and the subsequent transition to nuclei of the order of 10 ms. It should be noted that the average size of nuclei is about 10 nm.
Saturation
Regarding supersaturation coefficients for the nucleation of AgCl particles in open systems in which high concentrations of reactants such as AgNO3 and KCl are continuously introduced into the gelatin solution throughout the precipitation, Strong and Wey31 reported 1.029 (80° C) - 1.260 (40°C) and Leubner32 reported 1.024 at 60°C as estimated from measuring the growth rate of AgCl seed particles at critical supersaturation. This is the essence of the conductometric method of quantitative analysis.
On the other hand, for open AgBr particle systems, someestimated values of the critical supersaturation coefficient, Scrit: Scrit∼- 1.5 at 70 °C according to Wey and Strong33 from the size-dependent maximum growth rate determined by finding the renucleation threshold at different rates of adding an AgNO3 solution to a KBr solution in the presence of seed particles by the double jets; Scrit=1.2-1.5 at 25°C according to Jagannathan and Wey34 as the maximum supersaturation factor determined from the Gibbs-Thomson equation with their data on the minimum average size of nuclei observed by electron microscopy during the nucleation step of two-jet AgBr precipitation. This is very effective when applying the conductometric quantitation method.

When calculating these Scrit values, they took γ=140 mJ m − 2. Since nucleation in open systems corresponds to the process of survival of nascent nuclei created in a local zone of extremely high supersaturation near the reactant outlets, critical supersaturation corresponds to the concentration of the solute in equilibrium with nuclei of maximum size, if we use Sugimoto35's data on the maximum radius of AgBr nuclei in open systems (.3 8.3 nm) with theoretical γ for cubic AgBr (=109 mJ m − 2) 3, then the critical supersaturation factor, Scrit, is calculated as would be 1.36 at 25°C (if γ is assumed to be 140 mJ/m2, then Scrit=1.48).
Consequently, in any case, critical supersaturations inopen systems of silver halide particles are typically well below the maximum supersaturations (probably close to critical supersaturations) in closed systems. This is because the average radius of nuclei generated in the local zone of an open system is much larger than rmin a closed system, probably due to the instantaneous fusion of highly concentrated primary nuclei in the local zone of an open system with a high local electrolyte concentration.
Application
The use of the conductometric titration method for continuous recording during enzymatic processes has been extensively studied and analyzed. Almost all electrochemical analytical methods are based on electrochemical reactions (potentiometry, voltammetry, amperometry, coulometry).
The conductometric method of analysis is a method in which either there are no electrochemical reactions on the electrodes at all, or there are secondary reactions that can be neglected. Therefore, in this method, the most important property of the electrolyte solution in the boundary layer is its electrical conductivity, which varies according to a fairly wide range of biological reactions.
Benefits
Conductometric biosensors also have some advantages over other types of transducers. First, they can be made using low cost thin film standard technology. This, along with the use of an optimized method for immobilizing biological material, leads to a significant reduction in both the primary cost of devices andtotal cost of analysis. For built-in microbiosensors, it is easy to perform differential measurement mode, which compensates for external influences and greatly improves measurement accuracy.
The data clearly show the great potential of conductometric biosensors. However, this is still a fairly new trend in biosensors, so commercial device development has a promising future.
New methods
Some scientists have described a general method for measuring pKa by conductance. This method was widely used until about 1932 (before pH measurement methods were used). The conductometric method is extremely sensitive to temperature and cannot be used to measure overlapping pKa values. A possible advantage for samples without a chromophore is that it can be used in very dilute solutions, down to 2.8 × 10-5 M. In recent years, conductometry 87 has been used to measure the pKa of lidocaine, although the result obtained was 0.7 per unit below the generally accepted pH value.

Albert and Sergeant also described a method for determining pKa from solubility measurements. As mentioned above, solubility is dependent on pKa, so if solubility is measured at multiple pH values on a curve, pKa can be determined. Peck and Benet described a general method for estimating pKa values for monoprotic, diprotic, and amphoteric substances given a set of solubility and pH measurements. Hansen and Hafliger obtained the pKa of the sample, whichrapidly decomposes by hydrolysis from its initial dissolution rates as a function of pH in a rotating disc device. The result agrees well with the pH/UV result, but decomposition makes the latter method difficult. This is, by and large, a description of the conductometric method of analysis.






