Mathematics is not a boring science, as it seems sometimes. It has a lot of interesting, although sometimes incomprehensible for those who are not eager to understand it. Today we will talk about one of the most common and simple topics in mathematics, or rather, its area that is on the verge of algebra and geometry. Let's talk about lines and their equations. It would seem that this is a boring school topic that does not promise anything interesting and new. However, this is not the case, and in this article we will try to prove our point of view to you. Before moving on to the most interesting and describing the equation of a straight line through two points, we will turn to the history of all these measurements, and then find out why it was all necessary and why now the knowledge of the following formulas will not hurt either.
History
Even in ancient times, mathematicians were fond of geometric constructions and all kinds of graphs. It is difficult today to say who was the first to come up with the equation of a straight line through two points. But it can be assumed that this person was Euclid -ancient Greek scientist and philosopher. It was he who in his treatise "Beginnings" gave rise to the basis of the future Euclidean geometry. Now this section of mathematics is considered the basis of the geometric representation of the world and is taught at school. But it is worth saying that Euclidean geometry operates only at the macro level in our three-dimensional dimension. If we consider space, then it is not always possible to imagine with the help of it all the phenomena that occur there.
After Euclid there were other scientists. And they perfected and comprehended what he discovered and wrote. In the end, a stable area of geometry turned out, in which everything still remains unshakable. And it has been proven for thousands of years that the equation of a straight line through two points is very easy and simple to compose. But before we start explaining how to do this, let's discuss some theory.
Theory
A straight line is a segment infinite in both directions, which can be divided into an infinite number of segments of any length. In order to represent a straight line, graphs are most often used. Moreover, graphs can be in both two-dimensional and three-dimensional coordinate systems. And they are built according to the coordinates of the points belonging to them. After all, if we consider a straight line, we can see that it consists of an infinite number of points.
However, there is something in which a straight line is very different from other types of lines. This is her equation. In general terms, it is very simple, in contrast to, say, the equation of a circle. Surely, each of us went through it in school. Butnevertheless, let's write down its general form: y=kx+b. In the next section, we will analyze in detail what each of these letters means and how to solve this simple equation of a straight line passing through two points.
Line Equation
The equality that was presented above is the straight line equation we need. It is worth explaining what is meant here. As you might guess, y and x are the coordinates of each point on the line. In general, this equation exists only because each point of any straight line tends to be in connection with other points, and therefore there is a law that relates one coordinate to another. This law determines how the equation of a straight line through two given points looks like.
Why exactly two dots? All this is because the minimum number of points required to construct a straight line in two-dimensional space is two. If we take a three-dimensional space, then the number of points required to construct a single straight line will also be equal to two, since three points already make up a plane.
There is also a theorem proving that it is possible to draw a single straight line through any two points. This fact can be verified in practice by connecting two random points on the chart with a ruler.
Now let's look at a specific example and show how to solve this notorious equation of a straight line passing through two given points.
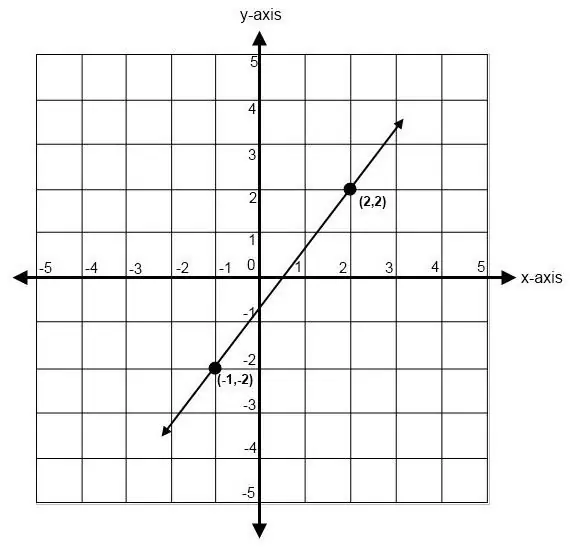
Example
Consider two points throughwhich you need to build a straight line. Let's set their coordinates, for example, M1(2;1) and M2(3;2). As we know from the school course, the first coordinate is the value along the OX axis, and the second one is the value along the OY axis. Above, the equation of a straight line through two points was given, and in order for us to find out the missing parameters k and b, we need to compose a system of two equations. In fact, it will be composed of two equations, each of which will contain our two unknown constants:
1=2k+b
2=3k+b
Now the most important thing remains: to solve this system. This is done quite simply. First, let's express b from the first equation: b=1-2k. Now we need to substitute the resulting equality into the second equation. This is done by replacing b with the equality we received:
2=3k+1-2k
1=k;
Now that we know what the value of the coefficient k is, it's time to find out the value of the next constant - b. This is made even easier. Since we know the dependence of b on k, we can substitute the value of the latter into the first equation and find out the unknown value:
b=1-21=-1.
Knowing both coefficients, now we can substitute them into the original general equation of a straight line through two points. Thus, for our example, we get the following equation: y=x-1. This is the desired equality, which we had to get.
Before moving on to the conclusion, let's discuss the application of this section of mathematics in everyday life.
Application
As such, the equation of a straight line through two points does not find application. But that doesn't mean we don't need it. In physics and mathematicsthe equations of lines and the properties that follow from them are very actively used. You may not even notice it, but mathematics is all around us. And even such seemingly unremarkable topics as the equation of a straight line through two points turn out to be very useful and very often applied at a fundamental level. If at first glance it seems that this can not be useful anywhere, then you are mistaken. Mathematics develops logical thinking, which will never be superfluous.
Conclusion
Now that we've figured out how to draw lines from two given points, it doesn't cost us anything to answer any question related to this. For example, if the teacher tells you: "Write the equation of a straight line passing through two points," then it will not be difficult for you to do this. We hope you found this article helpful.






