Solid material represents one of the four states of aggregation in which the matter around us can be. In this article, we will consider what mechanical properties are inherent in solids, taking into account the peculiarities of their internal structure.
What is a solid material?
Perhaps everyone can answer this question. A piece of iron, a computer, cutlery, cars, planes, stone, snow are all examples of solids. From a physical point of view, the solid aggregate state of matter is understood as its ability to retain its shape and volume under various mechanical influences. It is these mechanical properties of solids that distinguish them from gases, liquids, and plasmas. Note that the fluid also retains volume (is incompressible).
The above examples of solid materials will help to understand more clearly what an important role they play for human life and the technological development of society.
There are several physical and chemical disciplines that study the state of matter under consideration. We list only the most important of them:
- solid physicsbody;
- deformation mechanics;
- materials science;
- solid chemistry.
Structure of hard materials
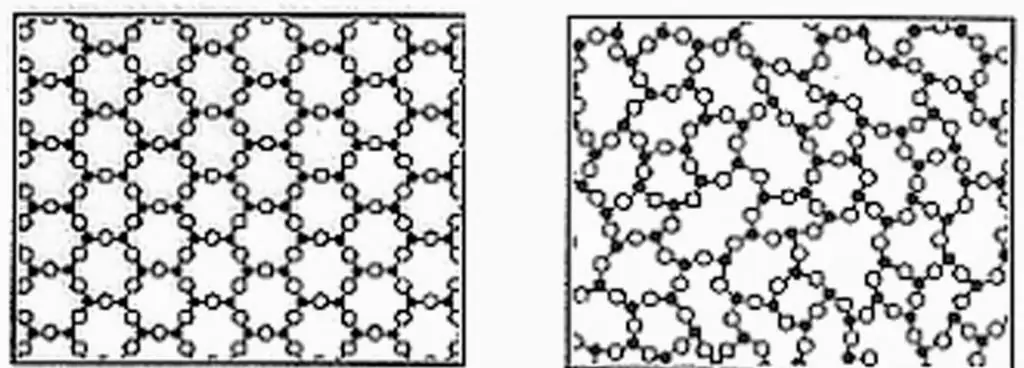
Before considering the mechanical properties of solids, one should get acquainted with their internal structure at the atomic level.
The variety of solid materials in their structure is great. Nevertheless, there is a universal classification, which is based on the criterion of the periodicity of the arrangement of the elements (atoms, molecules, atomic clusters) that make up the body. According to this classification, all solids are divided into the following:
- crystalline;
- amorphous.
Let's start with the second. An amorphous body does not have any ordered structure. Atoms or molecules in it are arranged randomly. This feature leads to the isotropy of the properties of amorphous materials, that is, the properties do not depend on the direction. The most striking example of an amorphous body is glass.
Crystalline bodies or crystals, unlike amorphous materials, have an arrangement of structural elements ordered in space. On the microscale, one can distinguish crystal planes and parallel atomic rows. Due to this structure, the crystals are anisotropic. Moreover, anisotropy manifests itself not only in the mechanical properties of solids, but also in the properties of electrical, electromagnetic, and others. For example, a tourmaline crystal can only transmit vibrations of a light wave in one direction, which leads topolarization of electromagnetic radiation.
Examples of crystals are almost all metallic materials. They are most often found in three crystal lattices: face-centered and body-centered cubic (fcc and bcc, respectively) and hexagonal close-packed (hcp). Another example of crystals is common table s alt. Unlike metals, its nodes contain not atoms, but chloride anions or sodium cations.
Elasticity is the main property of all hard materials

By applying even the smallest stress to a solid, we cause it to deform. Sometimes the deformation can be so small that it can not be noticed. However, all solid materials deform when an external load is applied. If, after removing this load, the deformation disappears, then they speak of the elasticity of the material.
A vivid example of the phenomenon of elasticity is the compression of a metal spring, which is described by Hooke's law. Through the force F and the absolute tension (compression) x, this law is written as follows:
F=-kx.
Here k is some number.
In the case of bulk metals, Hooke's law is usually written in terms of the applied external stress σ, relative strain ε and Young's modulus E:
σ=Eε.
Young's modulus is a constant value for a particular material.
Feature of elastic deformation, which distinguishes it from plastic deformation, is reversibility. Relative changes in the size of solids under elastic deformation do not exceed 1%. Most often they lie in the region of 0.2%. The elastic properties of solids are characterized by the absence of displacement of the positions of structural elements in the crystal lattice of the material after the termination of the external load.
If the external mechanical force is large enough, then after the termination of its action on the body, you can see the residual deformation. It's called plastic.
Plasticity of solids
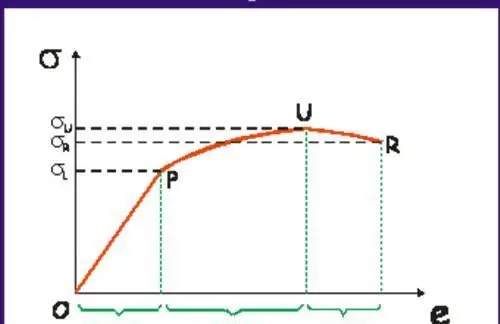
We have considered the elastic properties of solids. Now let's move on to the characteristics of their plasticity. Many people know and have observed that if you hit a nail with a hammer, it becomes flattened. This is an example of plastic deformation. At the atomic level, it is a complex process. Plastic deformation cannot occur in amorphous bodies, so the glass does not deform when it is hit, but collapses.
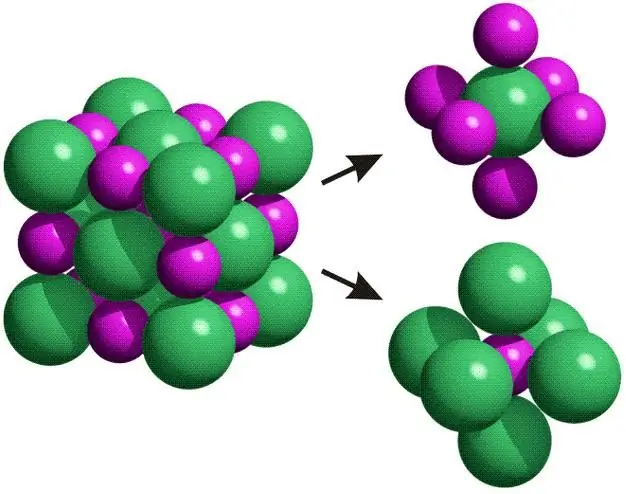
Solid bodies and their ability to plastically deform depends on the crystalline structure. The irreversible deformation under consideration occurs due to the movement of special atomic complexes in the volume of the crystal, which are called dislocations. The latter can be of two types (marginal and screw).
Of all solid materials, metals have the greatest plasticity, since they provide a large number of slip planes directed at different angles in space for dislocations. Conversely, materials with covalent or ionic bonds will be brittle. These can be attributedgems or the mentioned table s alt.
Brittleness and toughness
If you constantly apply an external force to any solid material, then sooner or later it will collapse. There are two types of destruction:
- fragile;
- viscous.
The first is characterized by the appearance and rapid growth of cracks. Brittle fractures lead to catastrophic consequences in production, therefore, they try to use materials and their operating conditions under which the destruction of the material would be ductile. The latter is characterized by slow crack growth and absorption of a large amount of energy before failure.
For each material there is a temperature that characterizes the brittle-ductile transition. In most cases, a decrease in temperature changes the fracture from ductile to brittle.
Cyclic and permanent loads
In engineering and physics, the properties of solids are also characterized by the type of load applied to them. So, a constant cyclic effect on the material (for example, tension-compression) is described by the so-called fatigue resistance. It shows how many cycles of application of a particular amount of stress the material is guaranteed to withstand without breaking.
Fatigue of a material is also studied under constant load, by measuring the strain rate over time.
Hardness of materials

One of the important mechanical properties of solids is hardness. She definesthe ability of the material to prevent the introduction of a foreign body into it. Empirically, it is very simple to determine which of the two bodies is harder. It is only necessary to scratch one of them with the other. Diamond is the hardest crystal. It will scratch any other material.
Other mechanical properties

Hard materials have some mechanical properties other than those noted above. We list them briefly:
- ductility - the ability to take on various shapes;
- ductility - the ability to stretch into thin threads;
- ability to resist special types of deformation, such as bending or twisting.
Thus, the microscopic structure of solids largely determines their properties.






