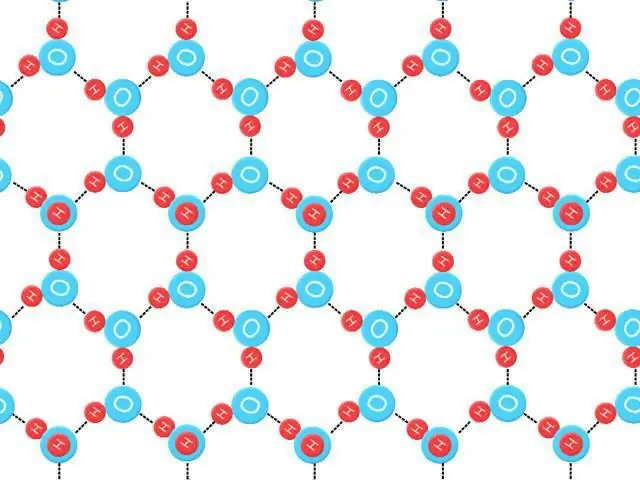
The three-dimensional state of liquid water is difficult to study, but much has been learned by analyzing the structure of ice crystals. Four neighboring hydrogen-interacting oxygen atoms occupy the vertices of a tetrahedron (tetra=four, hedron=plane). The average energy required to break such a bond in ice is estimated at 23 kJ/mol-1.

The ability of water molecules to form a given number of hydrogen chains, as well as a given strength, creates an unusually high melting point. When it melts, it is held by liquid water, the structure of which is irregular. Most of the hydrogen bonds are distorted. It takes a large amount of energy in the form of heat to break the crystal lattice of hydrogen-bonded ice.
Features of the appearance of ice (Ih)
Many of the inhabitants are wondering what kind of crystal lattice ice has. NecessaryIt should be noted that the density of most substances increases during freezing, when molecular movements slow down and densely packed crystals form. The density of water also increases as it cools to a maximum at 4°C (277K). Then, when the temperature falls below this value, it expands.
This increase is due to the formation of an open, hydrogen-bonded ice crystal with its lattice and lower density, in which each water molecule is rigidly bound by the above element and four other values, while moving fast enough to have more mass. Since this action occurs, the liquid freezes from top to bottom. This has important biological results, as a result of which the layer of ice on the pond insulates living beings away from extreme cold. In addition, two additional properties of water are related to its hydrogen characteristics: specific heat and evaporation.
Detailed description of structures
The first criterion is the amount needed to raise the temperature of 1 gram of a substance by 1°C. Raising the degrees of water requires a relatively large amount of heat because each molecule is involved in numerous hydrogen bonds that must be broken in order for the kinetic energy to increase. By the way, the abundance of H2O in the cells and tissues of all large multicellular organisms means that temperature fluctuations inside the cells are minimized. This feature is crucial, since the rate of most biochemical reactionssensitive.
The heat of vaporization of water is also significantly higher than that of many other liquids. A large amount of heat is required to convert this body into a gas, because the hydrogen bonds must be broken in order for the water molecules to dislocate from each other and enter the said phase. Changeable bodies are permanent dipoles and can interact with other similar compounds and those that ionize and dissolve.
Other substances mentioned above can come into contact only if polarity is present. It is this compound that is involved in the structure of these elements. In addition, it can align around these particles formed from electrolytes, so that the negative oxygen atoms of the water molecules are oriented to the cations, and the positive ions and hydrogen atoms are oriented to the anions.
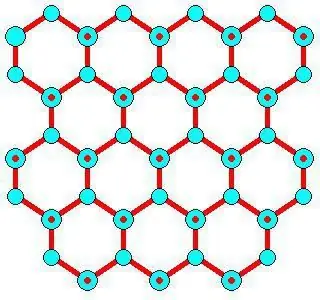
In solids, as a rule, molecular crystal lattices and atomic ones are formed. That is, if iodine is built in such a way that it contains I2, , then in solid carbon dioxide, that is, in dry ice, CO2 molecules are located at the crystal lattice nodes . When interacting with similar substances, ice has an ionic crystal lattice. Graphite, for example, which has an atomic structure based on carbon, is not able to change it, just like diamond.
What happens when a crystal of table s alt dissolves in water: polar molecules are attracted to charged elements in the crystal, which leads to the formation of similar particles of sodium and chloride on its surface, resulting in these bodiesare dislocated from each other, and it begins to dissolve. From here it can be observed that ice has a crystal lattice with ionic bonding. Each dissolved Na + attracts the negative ends of several water molecules, while each dissolved Cl - attracts the positive ends. The shell surrounding each ion is called the escape sphere and usually contains several layers of solvent particles.

Dry ice crystal lattice
Variables or an ion surrounded by elements are said to be sulfated. When the solvent is water, such particles are hydrated. Thus, any polar molecule tends to be solvated by the elements of the liquid body. In dry ice, the type of crystal lattice forms atomic bonds in the state of aggregation, which are unchanged. Another thing is crystalline ice (frozen water). Ionic organic compounds such as carboxylase and protonated amines must be soluble in hydroxyl and carbonyl groups. The particles contained in such structures move between molecules, and their polar systems form hydrogen bonds with this body.
Of course, the number of the last indicated groups in a molecule affects its solubility, which also depends on the reaction of various structures in the element: for example, one-, two- and three-carbon alcohols are miscible with water, but larger hydrocarbons with single hydroxyl compounds are much less dilute in liquids.
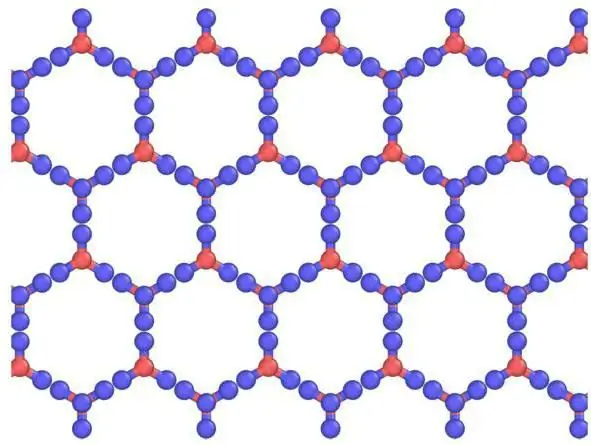
Hexagonal Ih is similar in shape toatomic crystal lattice. For ice and all natural snow on Earth, it looks exactly like this. This is evidenced by the symmetry of the crystal lattice of ice, grown from water vapor (that is, snowflakes). It is in space group P 63/mm from 194; D 6h, Laue class 6/mm; similar to β-, which has a multiple of 6 helical axis (rotation around in addition to shift along it). It has a fairly open low density structure where the efficiency is low (~1/3) compared to simple cubic (~1/2) or face centered cubic (~3/4) structures.
Compared to ordinary ice, the crystal lattice of dry ice, bound by CO2 molecules, is static and changes only when atoms decay.
Description of gratings and their elements
Crystals can be viewed as crystalline models, consisting of sheets placed one above the other. The hydrogen bond is ordered, while in reality it is random, since protons can move between water (ice) molecules at temperatures above about 5 K. Indeed, it is likely that protons behave like a quantum fluid in a constant tunneling flow. This is enhanced by the scattering of neutrons, showing their scattering density halfway between the oxygen atoms, indicating localization and coordinated motion. Here there is a similarity of ice with an atomic, molecular crystal lattice.
Molecules have a staggered arrangement of the hydrogen chainwith respect to its three neighbors in the plane. The fourth element has an eclipsed hydrogen bond arrangement. There is a slight deviation from perfect hexagonal symmetry, as the unit cell is 0.3% shorter in the direction of this chain. All molecules experience the same molecular environments. Inside each "box" there is enough space to hold particles of interstitial water. Although not generally considered, they have recently been effectively detected by neutron diffraction of the powdery crystal lattice of ice.
Changing Substances
The hexagonal body has triple points with liquid and gaseous water 0.01 ° C, 612 Pa, solid elements - three -21.985 ° C, 209.9 MPa, eleven and two -199.8 ° C, 70 MPa, as well as -34.7 ° C, 212.9 MPa. The dielectric constant of hexagonal ice is 97.5.
The melting curve of this element is given by MPa. The equations of state are available, in addition to them, some simple inequalities relating the change in physical properties to the temperature of hexagonal ice and its aqueous suspensions. Hardness fluctuates with degrees rising from or below gypsum (≦2) at 0°C to feldspar (6 Mohs) at -80°C, an abnormally large change in absolute hardness (> 24 times).
The hexagonal crystal lattice of ice forms hexagonal plates and columns, where the upper and lower faces are the basal planes {0 0 0 1} with an enthalpy of 5.57 μJ cm -2, and other equivalent side parts are called parts of the prism {1 0 -1 0} with 5, 94µJ cm -2. Secondary surfaces {1 1 -2 0} with 6.90 ΜJ ˣ cm -2 can be formed along the planes formed by the sides of the structures.
Such a structure shows an anomalous decrease in thermal conductivity with increasing pressure (as well as cubic and amorphous ice of low density), but differs from most crystals. This is due to a change in the hydrogen bond, which reduces the transverse speed of sound in the crystal lattice of ice and water.
There are methods describing how to prepare large crystal samples and any desired ice surface. It is assumed that the hydrogen bond on the surface of the hexagonal body under study will be more ordered than inside the bulk system. Variational spectroscopy with phase-lattice frequency generation has shown that there is a structural asymmetry between the two upper layers (L1 and L2) in the subsurface HO chain of the basal surface of hexagonal ice. The adopted hydrogen bonds in the upper layers of the hexagons (L1 O ··· HO L2) are stronger than those accepted in the second layer to the upper accumulation (L1 OH ··· O L2). Interactive hexagonal ice structures available.
Development Features
The minimum number of water molecules needed to form ice is approximately 275 ± 25, as for a complete icosahedral cluster of 280. Formation occurs at a rate of 10 10 at the air-water interface and not in bulk water. The growth of ice crystals depends on different growth rates of variousenergies. Water must be protected from freezing when cryopreserving biological specimens, food and organs.
This is typically achieved by fast cooling rates, using small samples and a cryoconservator, and increasing pressure to nucleate ice and prevent cell damage. The free energy of ice/liquid increases from ~30 mJ/m2 at atmospheric pressure to 40 mJ/m-2 at 200 MPa, indicating reason why this effect occurs.
What type of crystal lattice is characteristic of ice
Alternatively, they can grow faster from prism surfaces (S2), on the randomly disturbed surface of quick-frozen or agitated lakes. The growth from the {1 1 -2 0} faces is at least the same, but turns them into prism bases. The data on the development of the ice crystal have been fully investigated. The relative growth rates of elements of different faces depend on the ability to form a large degree of joint hydration. The temperature (low) of the surrounding water determines the degree of branching in the ice crystal. Particle growth is limited by the diffusion rate at a low degree of supercooling, i.e. <2 ° C, resulting in more of them.

But limited by development kinetics at higher levels of depression of >4°C, resulting in needle growth. This shape is similar to the structure of dry ice (has a crystal lattice with a hexagonal structure), variouscharacteristics of surface development and the temperature of the surrounding (supercooled) water, which is behind the flat shapes of snowflakes.
The formation of ice in the atmosphere profoundly affects the formation and properties of clouds. Feldspars, found in desert dust that enters the atmosphere in millions of tons per year, are important formers. Computer simulations have shown that this is due to the nucleation of prismatic ice crystal planes on high-energy surface planes.
Some other elements and lattices
Dissolved substances (with the exception of very small helium and hydrogen, which can enter the interstices) cannot be included in the Ih structure at atmospheric pressure, but are forced out to the surface or amorphous layer between the particles of the microcrystalline body. There are some other elements at the lattice sites of dry ice: chaotropic ions such as NH4 + and Cl -which are included in lighter liquid freezing than other cosmotropic ones such as Na + and SO42- , so removing them is not possible due to the fact that they form a thin film of the remaining liquid between the crystals. This can lead to electrical charging of the surface due to dissociation of the surface water balancing the remaining charges (which can also lead to magnetic radiation) and a change in the pH of the residual liquid films, e.g. NH 4 2SO4 becomes more acidic and NaCl becomes more basic.
They are perpendicular to the facescrystal lattice of ice showing the next layer attached (with O atoms in black). They are characterized by a slowly growing basal surface {0 0 0 1}, where only isolated water molecules are attached. The rapidly growing {1 0 -1 0} surface of a prism, where pairs of newly attached particles can bond with each other with hydrogen (one hydrogen bond/two molecules of an element). The fastest growing face is {1 1 -2 0} (secondary prismatic), where chains of newly attached particles can interact with each other by hydrogen bonding. One of her chain/element molecule is a shape that forms ridges that divide and encourage transformation into two sides of the prism.
Zero point entropy
Can be defined as S 0=k B ˣ Ln (N E0), where k B is the Boltzmann constant, NE is the number of configurations at the energy E, and E0 is the lowest energy. This value for the entropy of hexagonal ice at zero Kelvin does not violate the third law of thermodynamics "The entropy of an ideal crystal at absolute zero is exactly zero", since these elements and particles are not ideal, have disordered hydrogen bonding.
In this body, the hydrogen bond is random and rapidly changing. These structures are not exactly equal in energy, but extend to a very large number of energetically close states, obey the "rules of ice". Zero point entropy is the disorder that would remain even if the material could be cooled to absolutezero (0 K=-273, 15 ° C). Generates experimental confusion for hexagonal ice 3, 41 (± 0, 2) ˣ mol -1 ˣ K -1. Theoretically, it would be possible to calculate the zero entropy of known ice crystals with much greater accuracy (neglecting defects and energy level spread) than to determine it experimentally.
Scientists and their work in this area
Can be defined as S 0=k B ˣ Ln (N E0), where k B is the Boltzmann constant, NE is the number of configurations at the energy E, and E0 is the lowest energy. This value for the entropy of hexagonal ice at zero Kelvin does not violate the third law of thermodynamics "The entropy of an ideal crystal at absolute zero is exactly zero", since these elements and particles are not ideal, have disordered hydrogen bonding.
In this body, the hydrogen bond is random and rapidly changing. These structures are not exactly equal in energy, but extend to a very large number of energetically close states, obey the "rules of ice". Zero point entropy is the disorder that would remain even if the material could be cooled to absolute zero (0 K=-273.15°C). Generates experimental confusion for hexagonal ice 3, 41 (± 0, 2) ˣ mol -1 ˣ K -1. Theoretically, it would be possible to calculate the zero entropy of known ice crystals with much greater accuracy (neglecting defects and energy level spread) than to determine it experimentally.

Although the order of protons in bulk ice is not ordered, the surface probably prefers the order of these particles in the form of bands of hanging H-atoms and O-single pairs (zero entropy with ordered hydrogen bonds). The zero point disorder ZPE, J ˣ mol -1 ˣ K -1 and others is found. From all of the above, it is clear and understandable what types of crystal lattices are characteristic of ice.






