The movement of bodies in space is described by a set of characteristics, among which the main ones are the distance traveled, speed and acceleration. The latter characteristic largely determines the peculiarity and type of the movement itself. In this article, we will consider the question of what is acceleration in physics, and we will give an example of solving a problem using this value.
The main equation of dynamics
Before defining acceleration in physics, let's give the main equation of dynamics, which is called Newton's second law. It is often written as follows:
F¯dt=dp¯
That is, the force F¯, having an external character, had an effect on a certain body during the time dt, which led to a change in the momentum by the value dp¯. The left side of the equation is usually called the momentum of the body. Note that the quantities F¯ and dp¯ are vector in nature, and the vectors corresponding to them are directedthe same.
Each student knows the formula for the momentum, it is written as follows:
p¯=mv¯
The p¯ value characterizes the kinetic energy stored in the body (velocity factor v¯), which depends on the inertial properties of the body (mass factor m).
If we substitute this expression into the formula of Newton's 2nd law, we get the following equality:
F¯dt=mdv¯;
F¯=mdv¯ / dt;
F¯=ma¯, where a¯=dv¯ / dt.
The input value a¯ is called acceleration.
What is acceleration in physics?
Now let's explain what the value a¯ introduced in the previous paragraph means. Let's write down its mathematical definition again:
a¯=dv¯ / dt
Using the formula, one can easily understand that this is acceleration in physics. The physical quantity a¯ shows how quickly the speed will change with time, that is, it is a measure of the rate of change of the speed itself. For example, in accordance with Newton's law, if a force of 1 Newton acts on a body weighing 1 kilogram, then it will acquire an acceleration of 1 m / s2, that is, for every second of movement the body will increase its speed by 1 meter per second.
Acceleration and speed

In physics, these are two different quantities that are interconnected by kinematic equations of motion. Both quantities arevector, but in the general case they are directed differently. Acceleration is always directed along the direction of the acting force. The speed is directed along the trajectory of the body. The vectors of acceleration and velocity will coincide with each other only when the external force in the direction of action coincides with the movement of the body.
Unlike speed, acceleration can be negative. The latter fact means that it is directed against the movement of the body and seeks to reduce its speed, that is, the process of deceleration occurs.
The general formula that relates the modules of speed and acceleration looks like this:
v=v0+ at
This is one of the basic equations of rectilinear uniformly accelerated movement of bodies. It shows that over time the speed increases linearly. If the movement is equally slow, then a minus should be put in front of the term at. The value v0here is some initial speed.
With uniformly accelerated (equivalently slow) motion, the formula is also valid:
a¯=Δv¯ / Δt
It differs from a similar expression in differential form in that here the acceleration is calculated over a finite time interval Δt. This acceleration is called the average over the marked time period.
Path and acceleration
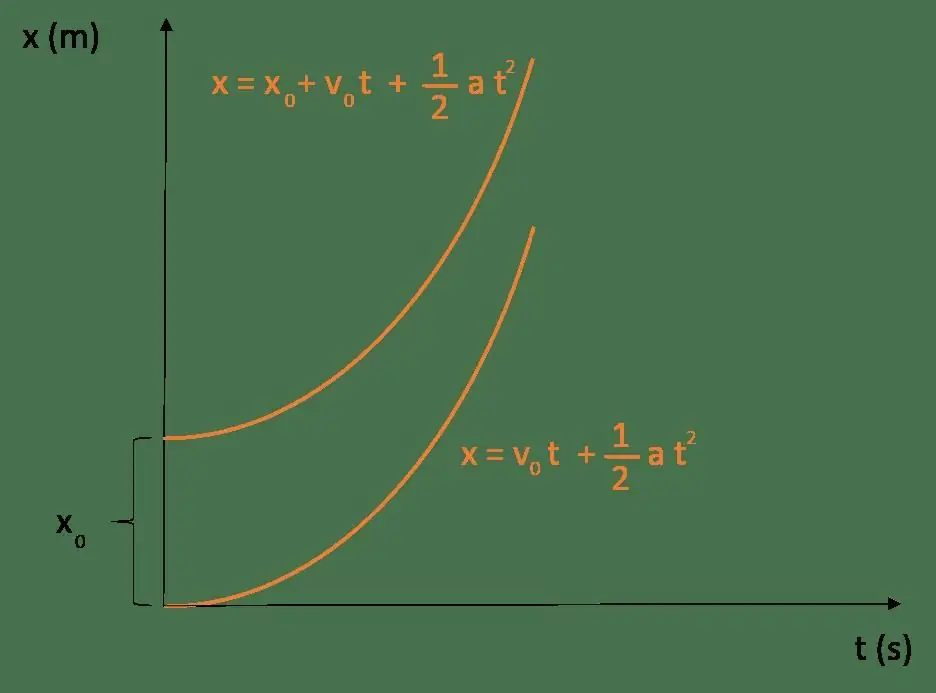
If the body moves uniformly and in a straight line, then the path traveled by it in time t can be calculated as follows:
S=vt
If v ≠ const, then when calculating the distance traveled by the body, acceleration should be taken into account. The corresponding formula is:
S=v0 t + at2 / 2
This equation describes uniformly accelerated motion (for uniformly slow motion, the "+" sign must be replaced by the "-" sign).
Circular motion and acceleration
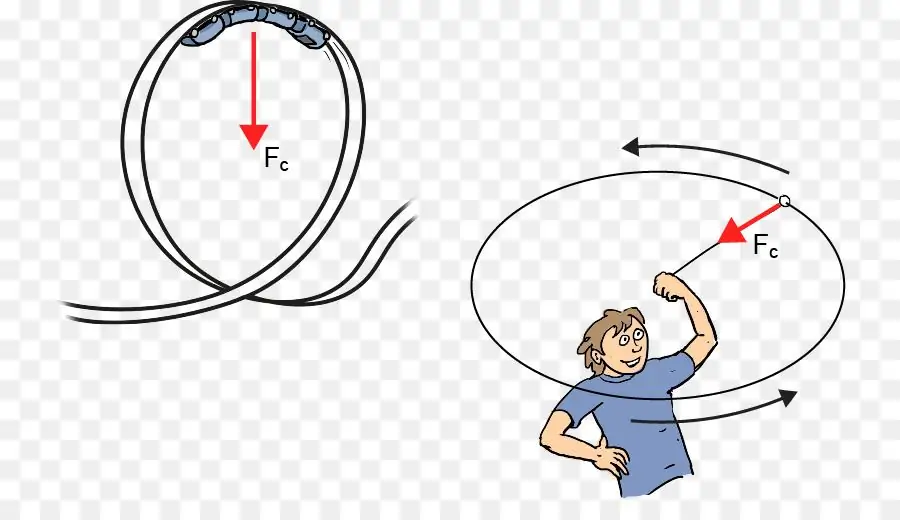
It was said above that acceleration in physics is a vector quantity, that is, its change is possible both in direction and in absolute value. In the case of the considered rectilinear accelerated motion, the direction of the vector a¯ and its modulus remain unchanged. If the module begins to change, then such a movement will no longer be uniformly accelerated, but will remain rectilinear. If the direction of the vector a¯ starts to change, then the motion will become curvilinear. One of the most common types of such movement is the movement of a material point along a circle.
Two formulas are valid for this type of movement:
α¯=dω¯ / dt;
ac=v2 / r
The first expression is the angular acceleration. Its physical meaning lies in the rate of change of the angular velocity. In other words, α shows how quickly the body spins up or slows down its rotation. The value α is a tangential acceleration, that is, it is directed tangentially to the circle.
The second expression describes the centripetal acceleration ac. If the linear rotation speedremains constant (v=const), then the module ac does not change, but its direction always changes and tends to direct the body towards the center of the circle. Here r is the radius of rotation of the body.
Problem with free fall of a body
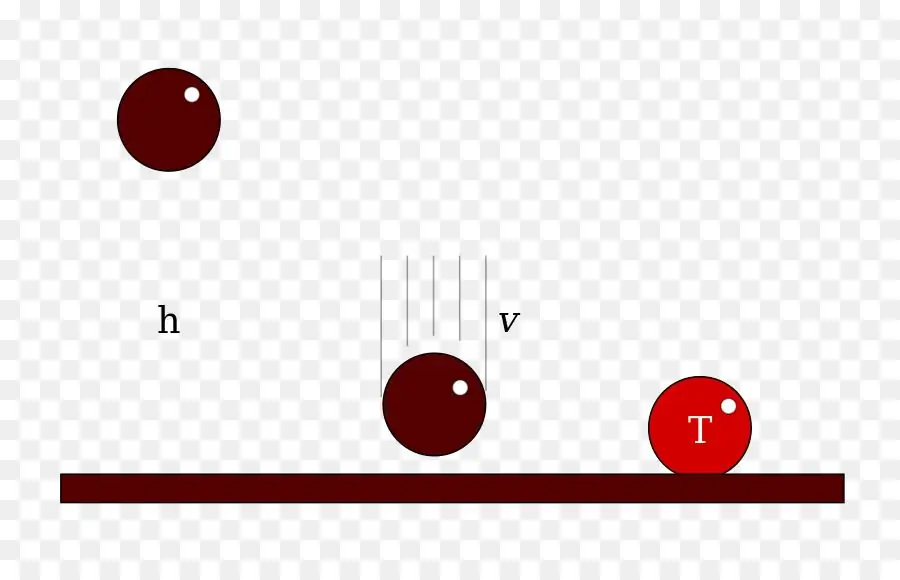
We found out that this is acceleration in physics. Now let's show how to use the above formulas for rectilinear motion.
One of the typical problems in physics with free fall acceleration. This value represents the acceleration that the gravitational force of our planet imparts to all bodies that have a finite mass. In physics, the free fall acceleration near the surface of the Earth is 9.81 m/s2.
Suppose that some body was at a height of 20 meters. Then he was released. How long will it take to reach the surface of the earth?
Since the initial speed v0is equal to zero, then for the distance traveled (height h) we can write the equation:
h=gt2 / 2
From where we get the fall time:
t=√(2h / g)
Substituting the data from the condition, we find that the body will be on the ground in 2.02 seconds. In reality, this time will be slightly longer due to the presence of air resistance.






