In the process of studying statics, which is one of the constituent sections of mechanics, the main role is given to axioms and basic concepts. There are only five basic axioms. Some of them are known from school physics lessons, because they are Newton's laws.
Definition of mechanics
First of all, it should be mentioned that statics is a subset of mechanics. The latter should be described in more detail, since it is directly related to statics. At the same time, mechanics is a more general term that combines dynamics, kinematics and statics. All these subjects were studied in the school physics course and are known to everyone. Even the axioms included in the study of statics are based on Newton's laws known from school years. However, there were three of them, while the basic axioms of statics are five. Most of them concern the rules for maintaining balance and rectilinear uniform movement of a certain body or material point.

Mechanics is the science of the simplest way to movematter - mechanical. The simplest movements are considered to be actions that are reduced to the movement in space and time of a physical object from one position to another.
What does mechanics study
In theoretical mechanics, the general laws of motion are studied without taking into account the individual properties of the body, except for the properties of extension and gravity (this implies the properties of particles of matter to be mutually attracted or have a certain weight).
The basic definitions include mechanical force. This term refers to the movement, mechanically transmitted from one body to the second during the interaction. According to numerous observations, it was determined that the force is considered a vector quantity, which is characterized by the direction and point of application.
In terms of the construction method, theoretical mechanics is similar to geometry: it is also based on definitions, axioms and theorems. Moreover, the connection does not end with simple definitions. Most of the drawings related to mechanics in general and statics in particular contain geometric rules and laws.
Theoretical mechanics includes three subsections: statics, kinematics and dynamics. In the first one, methods are studied for transforming forces applied to an object and an absolutely rigid body, as well as the conditions for the emergence of equilibrium. In kinematics, a simple mechanical movement is considered, which does not take into account the acting forces. In dynamics, the movements of a point, a system, or a rigid body are studied, taking into account the acting forces.
Axioms of statics
First, considerbasic concepts, axioms of statics, types of connections and their reactions. Statics is a state of equilibrium with forces that are applied to an absolutely rigid body. Its tasks include two main points: 1 - the basic concepts and axioms of statics include the replacement of an additional system of forces that were applied to the body by another system equivalent to it. 2 - derivation of general rules under which the body under the influence of applied forces remains in a state of rest or in the process of uniform translational rectilinear motion.
Objects in such systems are usually called a material point - a body whose dimensions can be omitted under the given conditions. A set of points or bodies interconnected in some way is called a system. The forces of mutual action between these bodies are called internal, and the forces affecting this system are called external.
The resultant force in a certain system is a force equivalent to the reduced system of forces. The forces that make up this system are called constituent forces. The balancing force is equal in magnitude to the resultant, but is directed in the opposite direction.
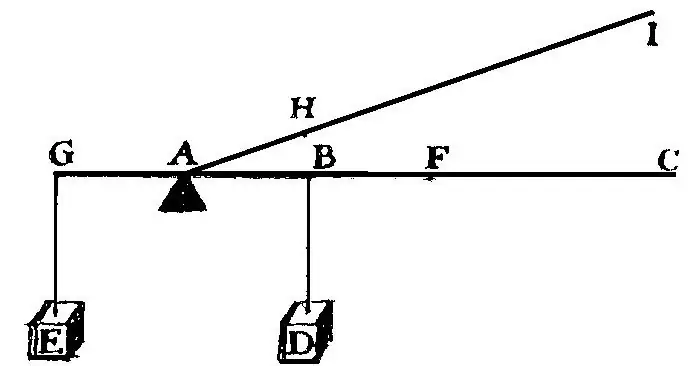
In statics, when solving the problem of changing the system of forces affecting a rigid body, or the balance of forces, geometric properties of force vectors are used. From this the definition of geometric statics becomes clear. Analytical statics based on the principle of admissible displacements will be described in dynamics.
Basic concepts and axiomsstatics
The conditions for a body to be in equilibrium are derived from several basic laws, used without additional evidence, but confirmed in the form of experiments, called the axioms of statics.
- Axiom I is called Newton's first law (axiom of inertia). Each body remains in a state of rest or uniform rectilinear motion until the moment when external forces act on this body, removing it from this state. This ability of the body is called inertia. This is one of the basic properties of matter.
- Axiom II - Newton's third law (the axiom of interaction). When one body acts on another with a certain force, the second body, together with the first, will act on it with a certain force, which is equal in absolute value, opposite in direction.
- Axiom III - the condition for the balance of two forces. To obtain the equilibrium of a free body, which is under the influence of two forces, it is sufficient that these forces be the same in their modulus and opposite in direction. This is also related to the next point and is included in the basic concepts and axioms of statics, the equilibrium of a system of descending forces.
- Axiom IV. Equilibrium will not be disturbed if a balanced system of forces is applied to or removed from a rigid body.
- Axiom V is the axiom of the parallelogram of forces. The resultant of two intersecting forces is applied at the point of their intersection and is represented by the diagonal of a parallelogram built on these forces.
Connections and their reactions
In the theoretical mechanics of a material point,Two definitions can be given to a system and a rigid body: free and non-free. The difference between these words is that if pre-specified restrictions are not imposed on the movement of a point, body or system, then these objects will by definition be free. In the opposite situation, objects are usually called non-free.
Physical circumstances leading to the restriction of freedom of named material objects are called links. In statics, there may be the simplest connections performed by different rigid or flexible bodies. The force of the bond action on a point, system or body is called the bond reaction.
Types of connections and their reactions
In ordinary life, the connection can be represented by threads, laces, chains or ropes. In mechanics, weightless, flexible and inextensible bonds are taken for this definition. Reactions, respectively, can be directed along a thread, a rope. At the same time, there are connections, the lines of action of which cannot be immediately determined. As an example of the basic concepts and axioms of statics, we can cite a fixed cylindrical hinge.
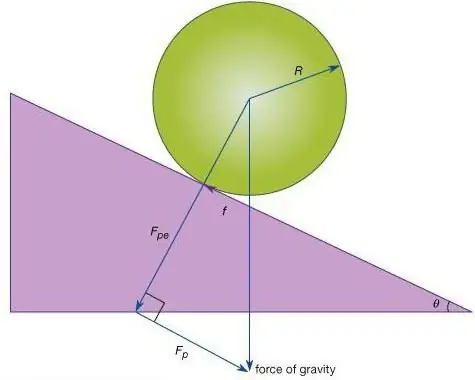
It consists of a fixed cylindrical bolt, on which a sleeve with a cylindrical hole is put on, the diameter of which does not exceed the size of the bolt. When the body is fastened to the bushing, the first can rotate only along the hinge axis. In an ideal hinge (provided that the friction of the surface of the sleeve and the bolt is neglected), an obstacle appears for the displacement of the sleeve in a direction perpendicular to the surface of the bolt and sleeve. For this reason, the reactionAn ideal hinge has a direction along the normal - the radius of the bolt. Under the influence of acting forces, the bushing is able to press against the bolt at an arbitrary point. In this regard, the direction of reaction at a fixed cylindrical hinge cannot be determined in advance. From this reaction, only its location in the plane perpendicular to the hinge axis can be known.
During the solution of problems, the hinge reaction will be established by the analytical method by expanding the vector. The basic concepts and axioms of statics include this method. The values of the reaction projections are calculated from the equilibrium equations. The same is done in other situations, including the impossibility of determining the direction of the bond reaction.
System of converging forces
The number of basic definitions can include a system of forces that converge. The so-called system of converging forces will be called a system in which the lines of action intersect at a single point. This system leads to a resultant or is in a state of equilibrium. This system is also taken into account in the previously mentioned axioms, since it is associated with maintaining the balance of the body, which is mentioned in several positions at once. The latter indicate both the causes necessary to create an equilibrium, and the factors that will not cause a change in this state. The resultant of this system of converging forces is equal to the vector sum of the named forces.
Equilibrium of the system
The system of converging forces is also included in the basic concepts and axioms of statics when studying. To find the system in equilibrium, the mechanical conditionbecomes zero value of the resultant force. Since the vector sum of the forces is zero, the polygon is considered closed.
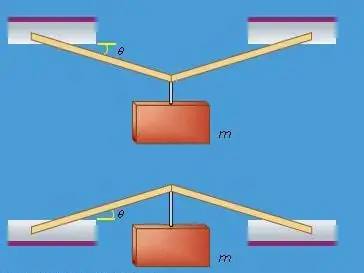
In an analytical form, the equilibrium condition of the system will be as follows: a spatial system of converging forces in equilibrium will have an algebraic sum of force projections on each of the coordinate axes equal to zero. Since in such an equilibrium situation the resultant will be zero, then the projections on the coordinate axes will also be zero.
Moment of force
This definition means the vector product of the force application point vector. The vector of the moment of force is directed perpendicular to the plane in which the force and the point lie, in the direction from which the rotation from the action of the force is seen to occur counterclockwise.
Pair of powers
This definition refers to a system consisting of a pair of parallel forces, equal in magnitude, directed in opposite directions and applied to a body.
The moment of a pair of forces can be considered positive if the forces of the pair are directed counterclockwise in the right-hand coordinate system, and negative - if they are directed clockwise in the left-hand coordinate system. When translating from the right coordinate system to the left one, the orientation of the forces is reversed. The minimum value of the distance among the lines of action of forces is called the shoulder. From this it follows that the moment of a pair of forces is a free vector, modulo equal to M=Fh and having perpendicular to the plane of actionthe direction that from the top of the given force vector were oriented positively.
Equilibrium in arbitrary systems of forces
The required equilibrium condition for an arbitrary spatial system of forces applied to a rigid body is the vanishing of the main vector and moment with respect to any point in space.
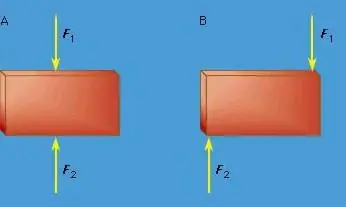
From this it follows that in order to achieve an equilibrium of parallel forces located in the same plane, it is required and sufficient that the resulting sum of the projections of forces on a parallel axis and the algebraic sum of all component moments provided by forces relative to a random point is equal to zero.
Center of gravity of the body
According to the law of universal gravitation, every particle in the vicinity of the Earth's surface is affected by attractive forces called gravity. With small dimensions of the body in all technical applications, one can consider the gravity forces of individual particles of the body as a system of practically parallel forces. If we consider all the forces of gravity of the particles to be parallel, then their resultant will be numerically equal to the sum of the weights of all particles, i.e. the weight of the body.
Subject of kinematics
Kinematics is a branch of theoretical mechanics that studies the mechanical motion of a point, a system of points and a rigid body, regardless of the forces affecting them. Newton, proceeding from a materialistic position, considered the nature of space and time to be objective. Newton used the definition of absolutespace and time, but separated them from moving matter, so he can be called a metaphysician. Dialectical materialism considers space and time as objective forms of existence of matter. Space and time without matter cannot exist. In theoretical mechanics it is said that the space including moving bodies is called three-dimensional Euclidean space.
Compared to theoretical mechanics, the theory of relativity is based on other concepts of space and time. This emergence of a new geometry created by Lobachevsky helped. Unlike Newton, Lobachevsky did not separate space and time from vision, considering the latter to be a change in the position of some bodies relative to others. In his own work, he pointed out that in nature, only movement is known to man, without which sensory representation becomes impossible. It follows from this that all other concepts, for example, geometric ones, are artificially created by the mind.
From this it is clear that space is considered as a manifestation of the connection between moving bodies. Almost a century before the theory of relativity, Lobachevsky pointed out that Euclidean geometry is related to abstract geometric systems, while in the physical world spatial relationships are determined by physical geometry, which differs from Euclidean, in which the properties of time and space are combined with the properties of matter moving in space. and time.
NotIt is worth noting that the leading scientists from Russia in the field of mechanics consciously adhered to the correct materialistic positions in the interpretation of all the main definitions of theoretical mechanics, in particular time and space. At the same time, the opinion about space and time in the theory of relativity is similar to the ideas about space and time of the supporters of Marxism, which were created before the emergence of works on the theory of relativity.
When working with theoretical mechanics during the measurement of space, the meter is taken as the main unit, and the second is taken as the time. Time is the same in each frame of reference and is independent of the alternation of these systems in relation to each other. Time is indicated by a symbol and is treated as a continuous variable value used as an argument. During the measurement of time, the definitions of the time interval, moment of time, initial time are applied, which are included in the basic concepts and axioms of statics.
Technical mechanics
In practical application, the basic concepts and axioms of statics and technical mechanics are interconnected. In technical mechanics, both the mechanical process of motion itself and the possibility of its use for practical purposes are studied. For example, when creating technical and building structures and testing them for strength, which requires a brief knowledge of the basic concepts and axioms of statics. At the same time, such a short study is suitable only for amateurs. In specialized educational institutions, this topic is of considerable importance, for example, in the case of a system of forces, basic concepts andaxioms of statics.

In technical mechanics, the above axioms are also applied. For example, axiom 1, basic concepts and axioms of statics are related to this section. While the very first axiom explains the principle of maintaining equilibrium. In technical mechanics, an important role is given not only to the creation of devices, but also to stable structures, in the construction of which stability and strength are the main criteria. However, it will be impossible to create something like this without knowing the basic axioms.
General remarks
The simplest forms of movement of solid bodies include translational and rotational motion of the body. In the kinematics of rigid bodies, for different types of motion, the kinematic characteristics of the movement of its different points are taken into account. The rotational movement of a body around a fixed point is such a movement in which a straight line passing through a pair of arbitrary points during the movement of the body remains at rest. This straight line is called the axis of rotation of the body.
In the text above, the basic concepts and axioms of statics were briefly given. At the same time, there is a large amount of third-party information with which you can better understand the statics. Do not forget the basic data, in most examples the basic concepts and axioms of statics include an absolutely rigid body, since this is a kind of standard for an object that may not be achievable under normal conditions.
Then we should remember the axioms. For example, the basic concepts and axiomsstatics, bonds and their reactions are among them. Despite the fact that many axioms only explain the principle of maintaining equilibrium or uniform motion, this does not negate their significance. Starting from the school course, these axioms and rules are studied, since they are Newton's well-known laws. The need to mention them is connected with the practical application of the knowledge of statics and mechanics in general. An example was technical mechanics, in which, in addition to creating mechanisms, it is required to understand the principle of designing sustainable buildings. Thanks to this information, the correct construction of ordinary structures is possible.






