Pyramid is a three-dimensional figure, the base of which is a polygon, and the sides are triangles. The hexagonal pyramid is its particular form. In addition, there are other variations when at the base of a triangle (such a figure is called a tetrahedron) there is a square, rectangle, pentagon, and so on in increasing order. When the number of points becomes infinite, a cone is obtained.
Hexagonal pyramid
In general, this is one of the latest and most complex topics in stereometry. It is studied somewhere in grades 10-11 and only the option is considered when the correct figure is at the base. One of the most difficult tasks in the exam is often associated with this paragraph.
And so, at the base of a regular hexagonal pyramid lies a regular hexagon. What does it mean? At the base of the figure, all sides are equal. The side parts consist of isosceles triangles. Their vertices touch at one point. This figureshown in the photo below.
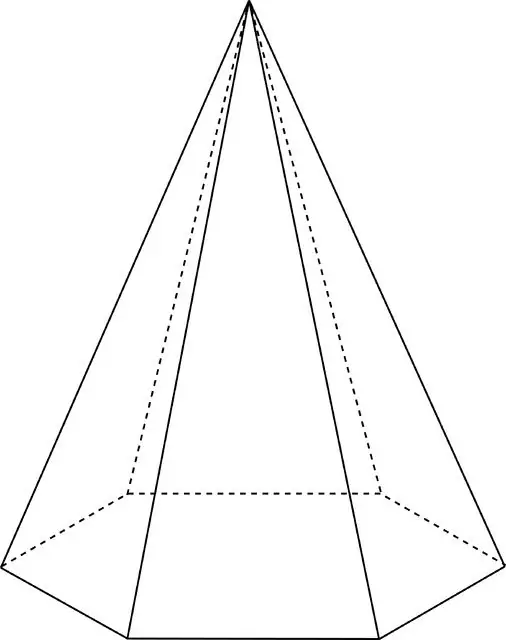
How to find the total surface area and volume of a hexagonal pyramid?
Unlike mathematics taught in universities, school science teaches to bypass and simplify some complex concepts. For example, if it is not known how to find the area of a figure, then you have to divide it into parts and find the answer using the already known formulas for the areas of the divided figures. This principle should be followed in the case presented.
That is, to find the surface area of the entire hexagonal pyramid, you need to find the area of the base, then the area of one of the sides and multiply it by 6.
The following formulas apply:
S (full)=6S (side) + S (base), (1);
S (bases)=3√3 / 2a2, (2);
6S (side)=6×1 / 2ab=3ab, (3);
S (full)=3ab + (3√3 / 2a2)=3(2a2b + √3) / 2a2, (4).
Where S is the area, cm2;
a - base length, cm;
b - apothem (height of side face), see
In order to find the area of the entire surface or any of its components, only the side of the base of the hexagonal pyramid and the apothem are required. If this is given in the problem in the condition, then the solution should not be difficult.
Things are much easier with volume, but to find it, you need the height (h) of the hexagonal pyramid itself. And, of course, the side of the base, thanks to which you need to find its area.
Formulalooks like this:
V=1/3 × S (bases) × h, (5).
Where V is volume, sm3;
h - figure height, see

Problem variant that can be caught on the exam
Condition. Given a regular hexagonal pyramid. The length of the base is 3 cm. The height is 5 cm. Find the volume of this figure.
Solution: V=1/3 × (3√3/2 × 32) × 5=5/3 × √3/6=5√3/18.
Answer: the volume of a regular hexagonal pyramid is 5√3/18 cm.






