Many motion problems in classical mechanics can be solved using the concept of the momentum of a particle or the entire mechanical system. Let's take a closer look at the concept of momentum, and also show how the knowledge gained can be used to solve physical problems.
The main characteristic of the movement
In the 17th century, when studying the movement of celestial bodies in space (the rotation of the planets in our solar system), Isaac Newton used the concept of momentum. In fairness, we note that a few decades earlier, Galileo Galilei had already used a similar characteristic when describing bodies in motion. However, only Newton was able to succinctly integrate it into the classical theory of the movement of celestial bodies developed by him.

Everyone knows that one of the important quantities characterizing the speed of change of body coordinates in space is speed. If it is multiplied by the mass of the moving object, then we get the mentioned amount of motion, that is, the following formula is valid:
p¯=mv¯
As you can see, p¯ isa vector quantity whose direction coincides with that of the velocity v¯. It is measured in kgm/s.
The physical meaning of p¯ can be understood by the following simple example: a truck is driving at the same speed and a fly is flying, it is clear that a person cannot stop a truck, but a fly can do it without problems. That is, the amount of movement is directly proportional not only to the speed, but also to the mass of the body (depends on the inertial properties).
Movement of a material point or particle
When considering many motion problems, the size and shape of a moving object often do not play a significant role in their solution. In this case, one of the most common approximations is introduced - the body is considered a particle or a material point. It is an immeasurable object, the entire mass of which is concentrated in the center of the body. This convenient approximation is valid when the dimensions of the body are much smaller than the distances it travels. A vivid example is the movement of a car between cities, the rotation of our planet in its orbit.
Thus, the state of the considered particle is characterized by the mass and speed of its movement (note that the speed may depend on time, that is, not be constant).
What is the momentum of a particle?
Often these words mean the amount of motion of a material point, that is, the value p¯. This is not entirely correct. Let's look at this issue in more detail, for this we write down the second law of Isaac Newton, which is already passed in the 7th grade of the school, we have:
F¯=ma¯
Knowing that acceleration is the rate of change of v¯ in time, we can rewrite it as follows:
F¯=mdv¯/dt=> F¯dt=mdv¯
If the acting force does not change with time, then the interval Δt will be equal to:
F¯Δt=mΔv¯=Δp¯
The left side of this equation (F¯Δt) is called the momentum of the force, the right side (Δp¯) is the change in momentum. Since the case of the motion of a material point is considered, this expression can be called the formula for the momentum of a particle. It shows how much its total momentum will change during the time Δt under the action of the corresponding force impulse.
Moment of momentum
Having de alt with the concept of the momentum of a particle of mass m for linear motion, let's move on to considering a similar characteristic for circular motion. If a material point, having a momentum p¯, rotates around the O axis at a distance r¯ from it, then the following expression can be written:
L¯=r¯p¯
This expression represents the angular momentum of the particle, which, like p¯, is a vector quantity (L¯ is directed according to the right-hand rule perpendicular to the plane built on the segments r¯ and p¯).
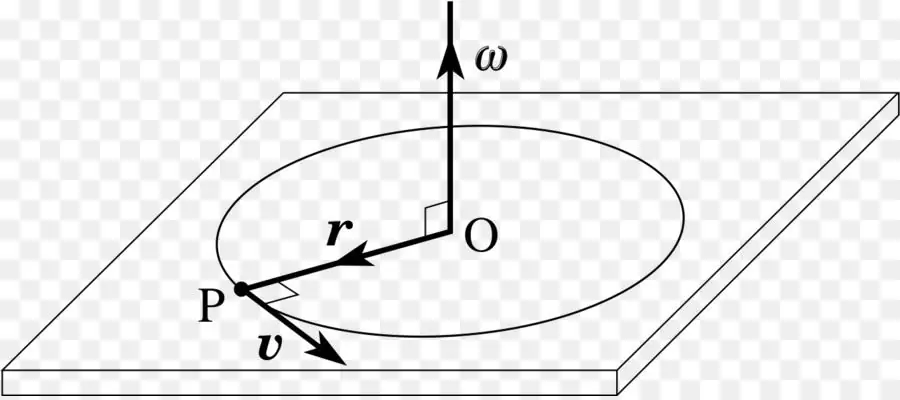
If the momentum p¯ characterizes the intensity of the body's linear displacement, then L¯ has a similar physical meaning only for a circular trajectory (rotation aroundaxis).
The formula for the angular momentum of a particle, written above, in this form is not used to solve problems. Through simple mathematical transformations, you can come to the following expression:
L¯=Iω¯
Where ω¯ is the angular velocity, I is the moment of inertia. This notation is similar to that for the linear momentum of a particle (the analogy between ω¯ and v¯ and between I and m).
Conservation laws for p¯ and L¯
In the third paragraph of the article, the concept of the impulse of an external force was introduced. If such forces do not act on the system (it is closed, and only internal forces take place in it), then the total momentum of the particles belonging to the system remains constant, that is:
p¯=const
Note that as a result of internal interactions, each momentum coordinate is preserved:
px=const.; py=const.; pz=const
Usually this law is used to solve problems with the collision of rigid bodies, such as balls. It is important to know that no matter what the nature of the collision (absolutely elastic or plastic), the total amount of motion will always remain the same before and after the impact.
Drawing a complete analogy with the linear movement of a point, we write the conservation law for the angular momentum as follows:
L¯=const. or I1ω1¯=I2ω2 ¯
That is, any internal changes in the moment of inertia of the system lead to a proportional change in the angular velocity of itsrotation.

Perhaps one of the common phenomena that demonstrates this law is the rotation of the skater on the ice, when he groups his body in different ways, changing his angular velocity.
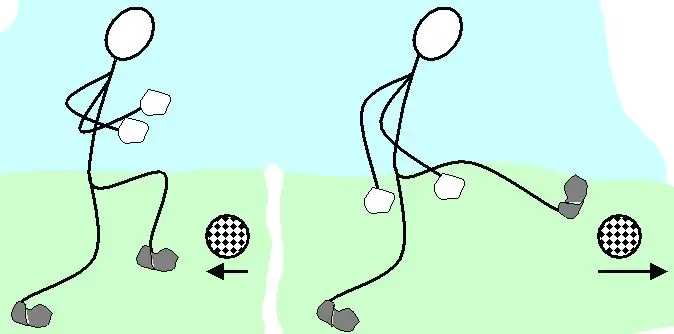
Two sticky balls collision problem
Let's consider an example of solving the problem of conservation of linear momentum of particles moving towards each other. Let these particles be balls with a sticky surface (in this case, the ball can be considered a material point, since its dimensions do not affect the solution of the problem). So, one ball moves along the positive direction of the X-axis with a speed of 5 m/s, it has a mass of 3 kg. The second ball moves along the negative direction of the X-axis, its speed and mass are 2 m/s and 5 kg, respectively. It is necessary to determine in which direction and with what speed the system will move after the balls collide and stick to each other.

The momentum of the system before the collision is determined by the difference in the momentum for each ball (the difference is taken because the bodies are directed in different directions). After the collision, the momentum p¯ is expressed by only one particle, the mass of which is equal to m1 + m2. Since the balls move only along the X axis, we have the expression:
m1v1 - m2v 2=(m1+m2)u
Where the unknown speed is from the formula:
u=(m1v1 -m2v2)/(m1+m2)
Substituting the data from the condition, we get the answer: u=0, 625 m/s. A positive velocity value indicates that the system will move in the direction of the X axis after the impact, and not against it.






