One of the most common types of movement of objects in space, which a person encounters every day, is uniformly accelerated rectilinear motion. In the 9th grade of general education schools in the course of physics, this type of movement is studied in detail. Consider it in the article.
Kinematic characteristics of movement

Before giving formulas describing uniformly accelerated rectilinear motion in physics, consider the quantities that characterize it.
First of all, this is the path traveled. We will denote it with the letter S. According to the definition, the path is the distance that the body has traveled along the trajectory of movement. In the case of rectilinear motion, the trajectory is a straight line. Accordingly, the path S is the length of the straight segment on this line. It is measured in meters (m) in the SI system of physical units.
Speed, or as it is often called linear speed, is the rate of change in body position inspace along its trajectory. Let's denote the speed as v. It is measured in meters per second (m/s).
Acceleration is the third important quantity for describing rectilinear uniformly accelerated motion. It shows how quickly the speed of the body changes in time. Symbolize acceleration as a and define it in meters per square second (m/s2).
The path S and the speed v are variable characteristics for rectilinear uniformly accelerated motion. Acceleration is a constant value.
Relationship between speed and acceleration
Let's imagine that some car is moving along a straight road without changing its speed v0. This movement is called uniform. At some point in time, the driver began to press the gas pedal, and the car began to increase its speed, acquiring acceleration a. If we start counting the time from the moment when the car acquired a non-zero acceleration, then the equation for the dependence of speed on time will take the form:
v=v0+ at.
Here the second term describes the increase in speed for each period of time. Since v0 and a are constant values, and v and t are variable parameters, the plot of the function v will be a straight line intersecting the y-axis at the point (0; v0), and having a certain angle of inclination to the abscissa axis (the tangent of this angle is equal to the acceleration value a).
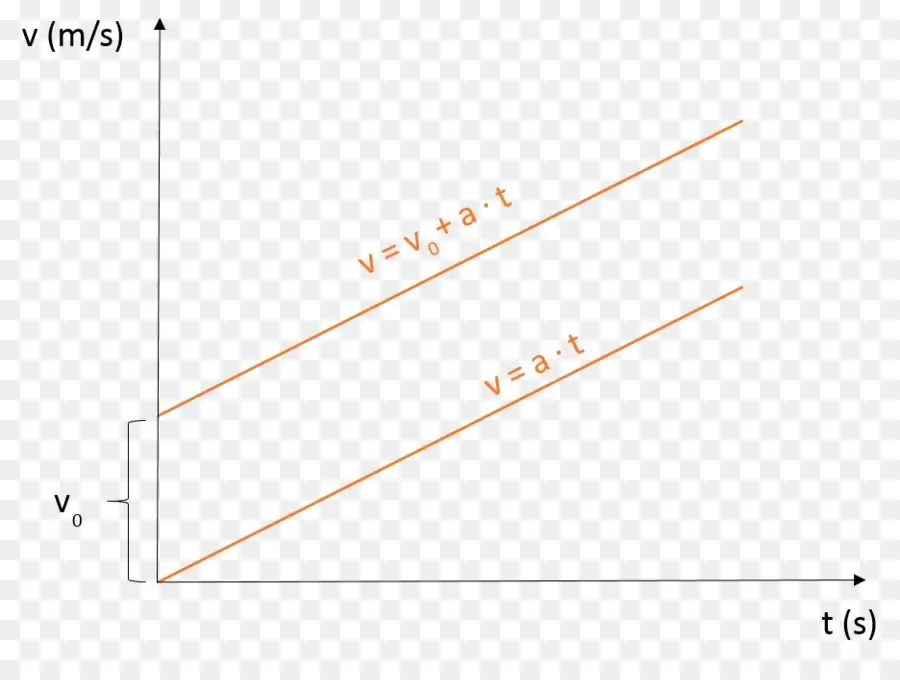
The figure shows two graphs. The only difference between them is that the top graph corresponds to the speed atthe presence of some initial value v0, and the lower one describes the speed of uniformly accelerated rectilinear motion when the body starts accelerating from rest (for example, a starting car).

Note, if in the example above the driver would press the brake pedal instead of the gas pedal, then the braking motion would be described by the following formula:
v=v0- at.
This type of movement is called rectilinear equally slow.
Formulas of the distance covered
In practice, it is often important to know not only the acceleration, but also the value of the path that the body passes over a given period of time. In the case of rectilinear uniformly accelerated motion, this formula has the following general form:
S=v0 t + at2 / 2.
The first term corresponds to uniform motion without acceleration. The second term is the net accelerated path contribution.
In case of braking of a moving object, the expression for the path will take the form:
S=v0 t - at2 / 2.
Unlike the previous case, here the acceleration is directed against the speed of movement, which leads to the latter turning to zero some time after the start of deceleration.
It is not difficult to guess that the graphs of the functions S(t) will be the branches of the parabola. The figure below shows these graphs in a schematic form.
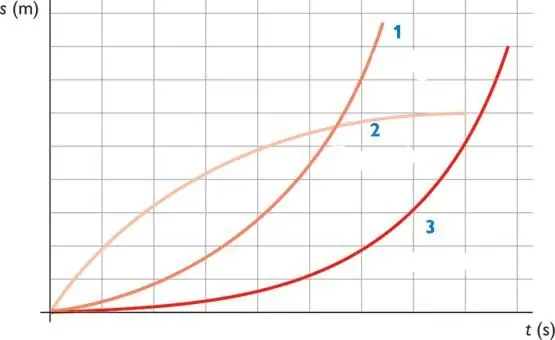
Parabolas 1 and 3 correspond to the accelerated movement of the body, parabola 2describes the braking process. It can be seen that the distance traveled for 1 and 3 is constantly increasing, while for 2 it reaches some constant value. The latter means that the body has stopped moving.
Further in the article, we will solve three different problems using the above formulas.
The task of determining the time of movement
The car must take the passenger from point A to point B. The distance between them is 30 km. It is known that a car moves with an acceleration of 1 m/s for 20 seconds2. Then its speed does not change. How long does it take for a car to take a passenger to point B?
The distance that the car will cover in 20 seconds will be:
S1=at12 / 2.
At the same time, the speed that he will pick up in 20 seconds is:
v=at1.
Then the desired travel time t can be calculated using the following formula:
t=(S - S1) / v + t1=(S - at 12 / 2) / (a t1) + t1.
Here S is the distance between A and B.
Let's convert all the known data to the SI system and substitute it into the written expression. We get the answer: t=1510 seconds or approximately 25 minutes.
The problem of calculating the braking distance
Now let's solve the problem of uniformly slow motion. Suppose a truck is moving at a speed of 70 km/h. Ahead, the driver saw a red traffic light and began to stop. What is the stopping distance of a car if it stopped in 15 seconds.
Stopping distance S can be calculated using the following formula:
S=v0 t - at2 / 2.
Deceleration time t and initial speed v0we know. The acceleration a can be found from the expression for the speed, given that its final value is zero. We have:
v0- at=0;
a=v0 / t.
Substituting the resulting expression into the equation, we arrive at the final formula for the path S:
S=v0 t - v0 t / 2=v0 t / 2.
Substitute the values from the condition and write down the answer: S=145.8 meters.
Problem to determine the speed in free fall

Perhaps the most common rectilinear uniformly accelerated motion in nature is the free fall of bodies in the gravitational field of planets. Let's solve the following problem: a body is released from a height of 30 meters. What speed will it have when it hits the ground?
The desired speed can be calculated using the formula:
v=gt.
Where g=9.81 m/s2.
Determine the fall time of the body from the corresponding expression for the path S:
S=gt2 / 2;
t=√(2S / g).
Substitute the time t into the formula for v, we get:
v=g√(2S / g)=√(2Sg).
The value of the path S traveled by the body is known from the condition, we substitute it into the equation, we get: v=24, 26 m/s or about 87km/h.






