Prism is one of the well-known figures studied in the course of solid geometry in secondary schools. To be able to calculate various characteristics for figures of this class, you need to know what types of prisms exist. Let's take a closer look at this issue.
Prism in stereometry
First of all, let's define the mentioned class of figures. A prism is any polyhedron consisting of two parallel polygonal bases, which are interconnected by parallelograms.
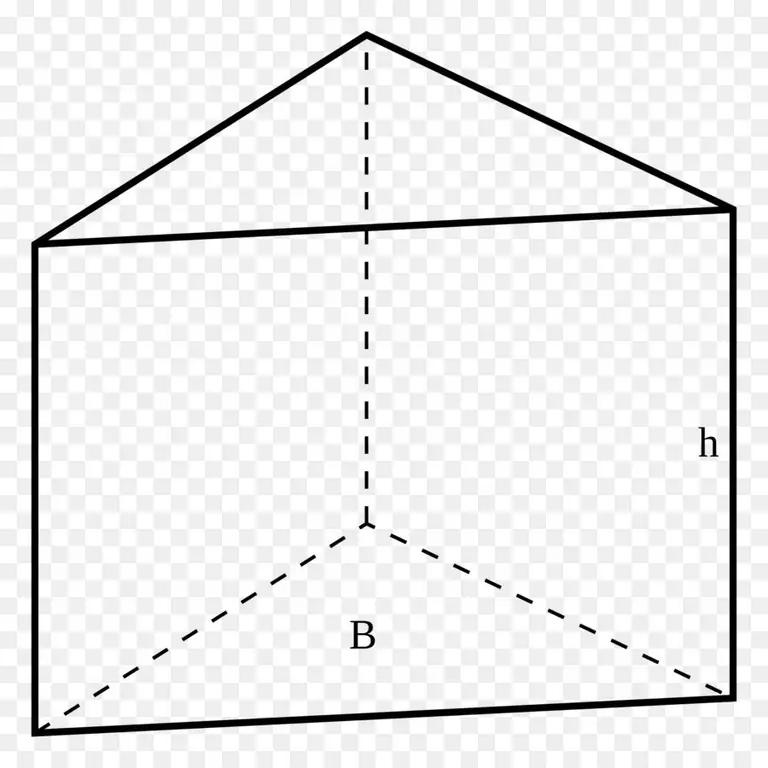
You can get this figure in the following way: select an arbitrary polygon on the plane, and then move it to the length of any vector that does not belong to the original plane of the polygon. During such a parallel movement, the sides of the polygon will describe the side faces of the future prism, and the final position of the polygon will become the second base of the figure. In the described way, an arbitrary type of prism can be obtained. The figure below shows a triangular prism.
What are the types of prisms?
It's about the classification of shapesthe class in question. In the general case, this classification is carried out taking into account the features of the polygonal base and the sides of the figure. Usually, the following three types of prisms are distinguished:
- Straight and oblique (oblique).
- Right and wrong.
- Convex and concave.
A prism of any of the named types of classification can have a quadrangular, pentagonal, …, n-gonal base. As for the types of triangular prism, it can only be classified according to the first two points mentioned. A triangular prism is always convex.
Below, we will take a closer look at each of these types of classification and give some useful formulas for calculating the geometric properties of a prism (surface area, volume).
Straight and Oblique Shapes
It is possible to distinguish a direct prism from an oblique one at a glance. Here is the corresponding figure.
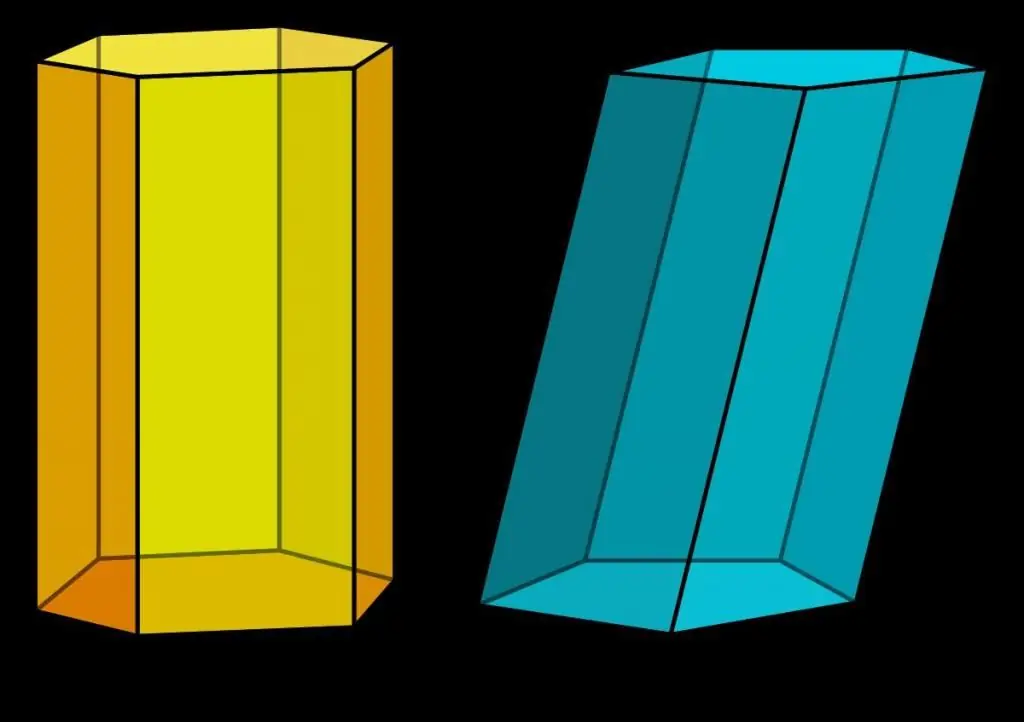
Here two prisms are shown (hexagonal on the left and pentagonal on the right). Everyone will say with confidence that the hexagonal is straight, and the pentagonal is oblique. What geometric feature distinguishes these prisms? Of course, the side face type.
A straight prism, regardless of its base, all faces are rectangles. They can be equal to each other, or they can differ, the only important thing is that they are rectangles, and their dihedral angles with bases are 90o.
Regarding an oblique figure, it should be said that all or some of its side faces areparallelograms that form indirect dihedral angles with the base.
For all types of straight prisms, the height is the length of the side edge, for oblique figures, the height is always less than their side edges. Knowing the height of a prism is important when calculating its surface area and volume. For example, the volume formula is:
V=Soh
Where h is the height, So is the area of one base.
Prisms correct and incorrect
Any prism is wrong if it is not straight or its base is not correct. The question of straight and inclined prisms was discussed above. Here we consider what the expression "regular polygonal base" means.
A polygon is regular if all its sides are equal (let's denote their length by letter a), and all its angles are also equal. Examples of regular polygons are an equilateral triangle, a square, a hexagon with six corners of 120o and so on. The area of any regular n-gon is calculated using this formula:
S=n/4a2ctg(pi/n)
Below is a schematic representation of regular prisms with triangular, square, …, octagonal bases.
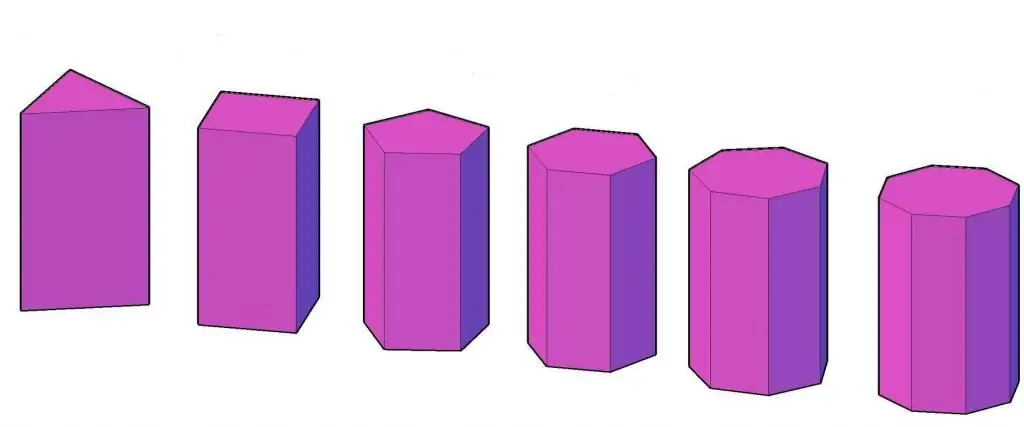
Using the above formula for V, we can write the corresponding expression for regular shapes:
V=n/4a2ctg(pi/n)h
As for the total surface area, for regular prisms it is formed by the areas of twoidentical bases and n identical rectangles with sides h and a. These facts allow us to write a formula for the surface area of any regular prism:
S=n/2a2ctg(pi/n) + nah
Here the first term corresponds to the area of the two bases, the second term determines the area of the lateral surface only.
Of all the types of regular prisms, only quadrangular prisms have their own names. So, a regular quadrangular prism, in which a≠h, is called a rectangular parallelepiped. If this figure has a=h, then they talk about a cube.
Concave shapes
Until now, we have considered only convex types of prisms. It is to them that the main attention is paid in the study of the class of figures under consideration. However, there are also concave prisms. They differ from convex ones in that their bases are concave polygons, starting from a quadrilateral.

The figure shows two concave prisms, which are made of paper, as an example. The left one in the form of a five-pointed star is a decagonal prism, the right one in the form of a six-pointed star is called a dodecagonal concave straight prism.






